特定字符搜索

Posted 2021-02-20 shouzhuo

问题

假如有一个4个字节的整型数据: b4|b3|b2|b1. 怎样快速的判断4个byte中是否存在某个特定byte? 一开始考虑的是使用bitwise operator. 但是始终没有想出来. (这些操作在bit之间的独立的, 我怀疑只使用这些操作是无法判断的). 在网上查了一下, 找到了一个方法, 是利用加法进位进行判断(姑且称之为进位判断方法). 这里写下自己的理解

进位判断方法("特定byte"这里为0)

算法

# v是四个字节的整型
t = v + 0x7efefeff;
n = ~v;
o = t ^ n;
r = o & (~0x7efefeff);

定义

  byte4     byte3     byte2     byte1
0111_1110 1111_1110 1111_1110 1111_1111  # 0x7efefeff
31     24        16         8

四个字节从高到低分别称为byte4, byte3, byte2, byte1
四个特殊的bit(31,24,16,8)称为holebits.

反向推导

1. 既然r==0, 那么o的holebits一定都是0
    => o[31]==0 && o[24]==0 && o[16]==0 && o[8]==0
2. 既然o的holebits都为0. 那么t和n的holebits一定相同.
    => t[31]==n[31] && t[24]==n[24] && t[16]==n[16] && t[8]==n[8]
3. 既然n是v的取反. 那么t和v的holebits一定不同.
    => t[31]!=v[31] && t[24]!=v[24] && t[16]!=v[16] && t[8]!=v[8]
3.1 既然t[8]!=v[8], 而t[8]=v[8]+0+carrybit. 所以carrybit必然为1. 也就是byte1求和时有进位.
    => v[byte1]>0
3.2 既然t[16]!=v[16], 而t[16]=v[16]+0+carrybit. 所以carrybit必然为1. 也就是byte2求和时有进位. 
    因此v[byte2]>1. 
    根据3.1知道, byte2还会收到byte1的进位. 因此
    => v[byte2]>0
3.3 既然t[24]!=v[24], 而t[24]=v[24]+0+carrybit. 所以carrybit必然为1. 也就是byte3求和时有进位. 
    因此v[byte3]>1. 
    根据3.2知道, byte3还会收到byte2的进位. 因此
    => v[byte3]>0
3.4 既然t[31]!=v[31], 而t[31]=v[31]+0+carrybit. 那么b[24:30]一定有进位. 
    因此v[24:30]>1
    根据3.3知道, byte3还会收到byte2的进位. 因此
    => v[24:30]>0

正向推导

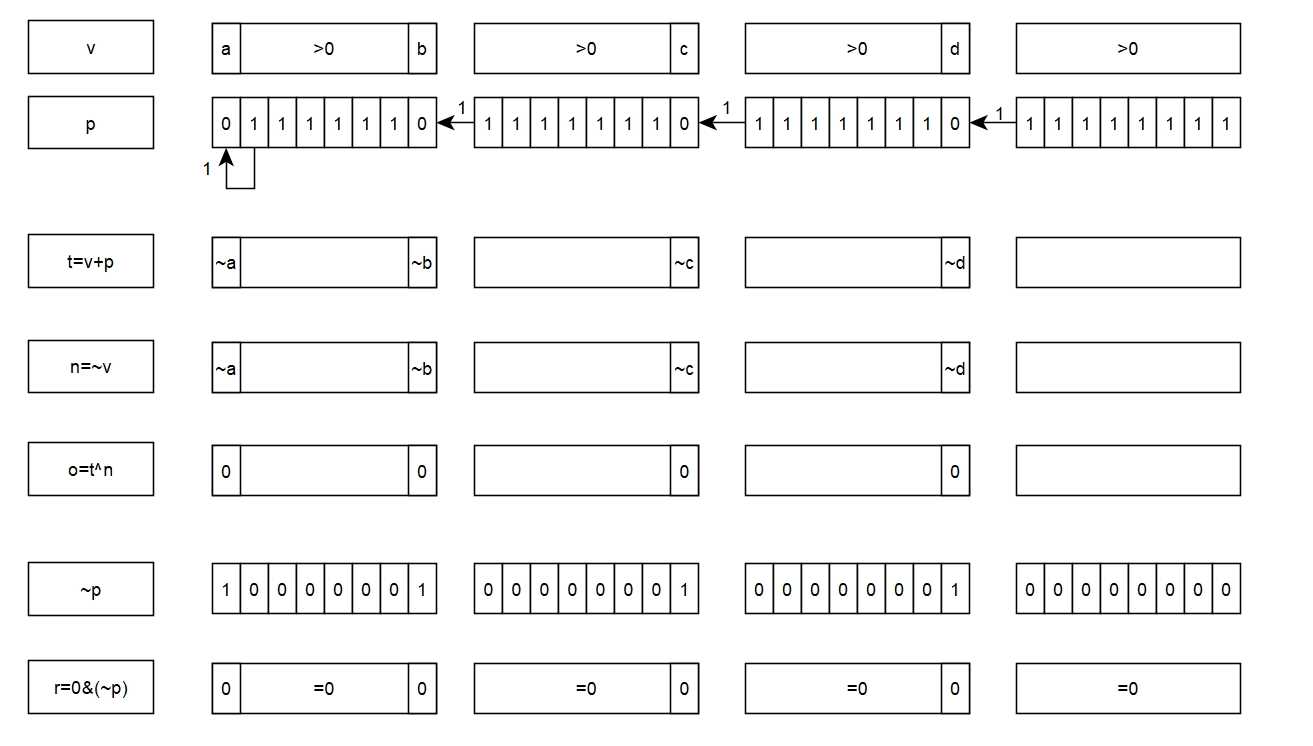
假定4个字节都>0. 由于byte1和0xff相加有进位, 这导致所有byte相加都有进位. 由于bit + 1 == ~bit.
=> t的holebits一定和v的holebits相反.
=> t的holebits一定和n的holebits相同.
=> o的holebits一定都是0
=> r的holebits一定都是0.
=> r==0

虽然指令增多, 但是都是对v的运算, 并没有额外的内存访问(严格来说多了几个指令本身的load). 但是条件分支降低了4倍. 实测有将近3倍以上的性能提升.
虽然我可以推导, 但是我完全搞不懂这到底是怎么想出来的.

C代码

#define bytes_has_zero_4(v) ((v+0x7efefeff)^(~v)) & (~0x7efefeff)
#define bytes_has_zero_8(v) ((v+0x7efefefefefefeff)^(~v)) & (~0x7efefefefefefeff)

判断其他值

上面方法只能判断一个整形中是否包含byte0. 如果要判断其他值, 需要先转化为判断byte0的问题.

uint32_t target=0x0A; // 需要检测的byte
uint32_t pattern = (target<<24)|(target<<16)|(target<<8)|target;
v0 = v ^ pattern; // 如果a==b, a^b==0. 否则a^b!=0.

该方法可以用来快速获取字符串长度, 或者按行切割字符串. 但是实际代码中需要注意

1. 需要先对齐
2. 会出现访问越界问题
   TODO 待补充