Matlab追赶法和迭代法解线性方程组

Posted 2021-02-20 jianle23

实验目的：

1）追赶法解三对角阵；

2）掌握解线性方程组的迭代法；

3）用Matlab实现Jacobi及超松弛迭代法

实验要求：

1）掌握追赶法解三对角阵

2）掌握解线性方程组的迭代法

3）提交追赶法、Jacobi及超松弛迭代法的m文件

实验内容：

1）追赶法解三对角矩阵方程（m文件）

 

习题1. 用追赶法的m文件求解

 

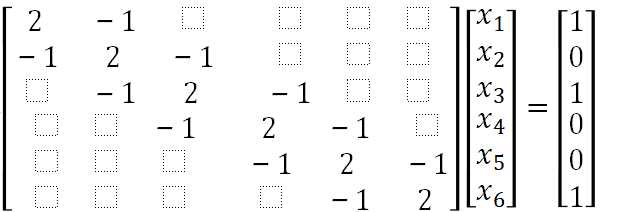
2）Jacobi迭代法解线性方程组（m文件）

 

对不同初值用Jacobi迭代法解习题1并比较结果。

 

 

3）超松弛迭代法解线性方程组（m文件）

 

对不同松弛因子解习题1并比较结果。

 

实验步骤：

　　

 

 

 　　代码：

 1 %追赶法
 2 %输入：系数矩阵A和因变量d；
 3 %输出：自变量x
 4 function z=zuigan(A,d)
 5 n=length(d);
 6 %取三对角元素a,b,c
 7 for i=1:n-1
 8     a(i)=A(i,i);
 9     b(i)=A(i+1,i);
10     c(i)=A(i,i+1);
11 end
12 a(n)=A(n,n);
13 %分解系数矩阵
14 u(1)=a(1);
15 l(1)=c(1)/a(1);
16 for i=2:n-1
17     u(i)=a(i)-b(i-1)*l(i-1);
18     l(i)=c(i)/u(i);
19 end
20 u(n)=a(n)-c(n-1)*l(n-1);
21 %解y
22 y(1)=d(1)/u(1);
23 for k=2:n
24     y(k)=d(k)-c(k-1)*y(k-1)/u(k);
25 end
26 %解x
27 x(n)=y(n);
28 for k=n-1:-1:1
29     x(k)=y(k)-l(k)*x(k+1);
30 end
31 z=x;
32 end

zuigan

　　运行：

　　

 

 

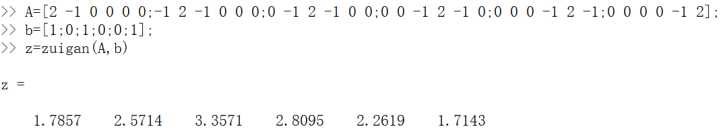
 　　所得结果，较为粗糙。

 

 

 

 　　代码：

 1 %雅克比迭代法
 2 %输入系数矩阵A，因变量b，初始向量x0,容许误差eps,最大迭代次数t
 3 %输出自变量x和迭代数n
 4 function [z,k]=jacobi(A,b,x0,e,t)
 5 %默认eps和最大迭代次数m
 6 if nargin==3
 7     e=1e-6;
 8     m=200;
 9 elseif nargin<3
10     error(‘输入的参数不足‘);
11     return;
12 elseif nargin==5
13     m=t;
14 end
15 n=length(b);
16 x(1,:)=x0;
17 z(1,:)=x0;
18 for k=2:m
19     sum=0;
20     for i=1:n
21         w=0;
22         u=0;
23         for j=i+1:n
24             w=w+A(i,j)*x(k-1,j);
25         end
26         for j=1:i-1
27             u=u+A(i,j)*x(k-1,j);
28         end
29         x(k,i)=(-1/A(i,i))*(u+w-b(i));
30         if sum<abs(x(k,i)-x(k-1,i))
31             sum=abs(x(k,i)-x(k-1,i));
32         end
33     end
34     if sum<e
35        z(k,:)=x(k,:);
36        return;
37     end
38     z(k,:)=x(k,:);
39 end
40 end

jacobi

　　运行示例，初始向量x0=[0 0 0 0 0 0];和初始向量x0=[1 1 1 1 1 1];

　　

 

 

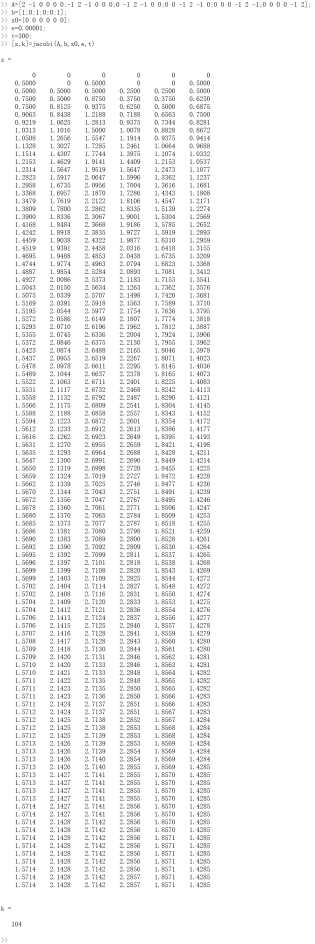
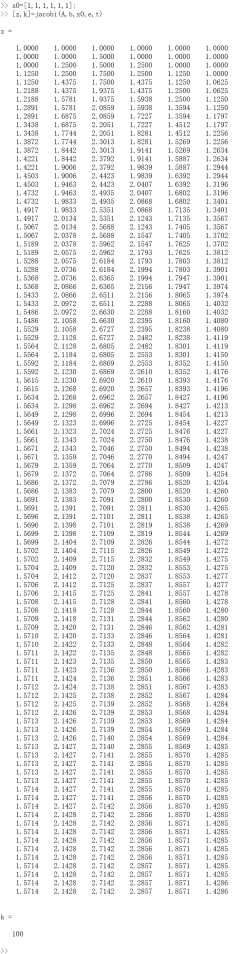
 　　初始值不同，迭代次数可能不同。

 

 

 

 

 　　代码：

 1 %---逐次超松弛迭代法-----
 2 %输入：系数矩阵A，因变量b，松弛因子w，精度eps
 3 %输出：自变量x，迭代次数k
 4 function [z,k]=sor(A,b,w,eps)
 5 N=length(b); %解向量的维数
 6 x=zeros(N,1);%迭代初始值
 7 %-----(A=D-E-F)------
 8 D=diag(diag(A));
 9 E=-tril(A,-1);%下三角
10 F=-triu(A,1);%上三角
11 B=inv(D-w*E)*((1-w)*D+w*F);g=w*inv(D-w*E)*b;
12 %--------开始迭代-------
13 for k=1:100 %最大迭代次数为100
14     y=B*x+g;
15     if abs(x-y)<eps
16         break;
17     end
18     x=y;
19     z(k,:)=x;
20 end
21 z(k,:)=x;
22 end

sor

　　运行示例，松弛因子w=1.1;和w=1.5；

 

 　　

 

 

　　 

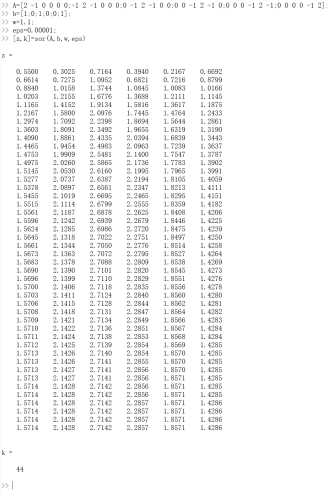
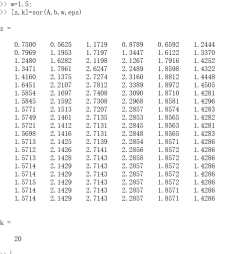
　　松弛因子不同，迭代次数可能不同。

 

小结：

　　在把数学步骤翻译为算法时，遵循语法规则是必要的；在算法翻译为程序代码时，需要对边界值做推敲。完成代码的编写，需要对它进行检验，特别是边界值的检验。