SPSS方差分析

Posted 2021-02-20 jianle23

实验目的：

1、学会使用SPSS的简单操作。

2、掌握方差分析。

实验内容：

1.单因素方差分析；

2.双因素方差分析。

实验步骤：

　　1.单因素方差分析，方差分析是基于变异分解的思想进行的，在单因数方差分析中，整个样本的变异可以看成由两个部分构成：总变异=随机变异+处理因数导致的变异，其中随机变异是永远存在的，确定处理因数导致的变异是否存在就是所要达到的研究目标，即只要能证明它不等于0，就等同于证明了处理因数的确存在影响。

　　

 

 

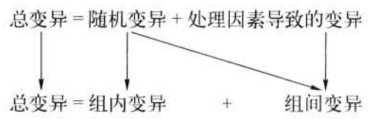
　　这样可采用一定的方法来比较组内变异和组间变异的大小，如果后者远远大于前者，则说明处理因数的影响的确存在，如果两者相差无几，则说明该影响不存在。

 

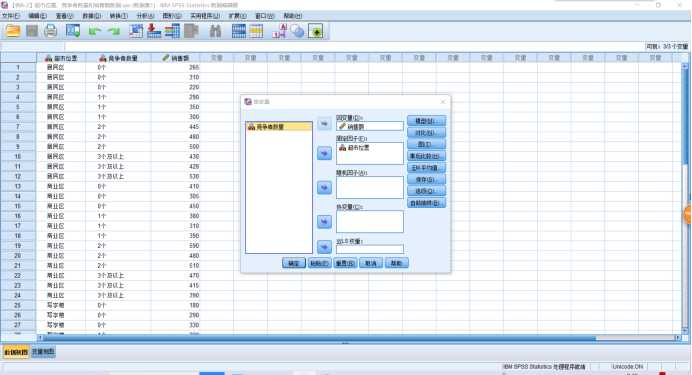
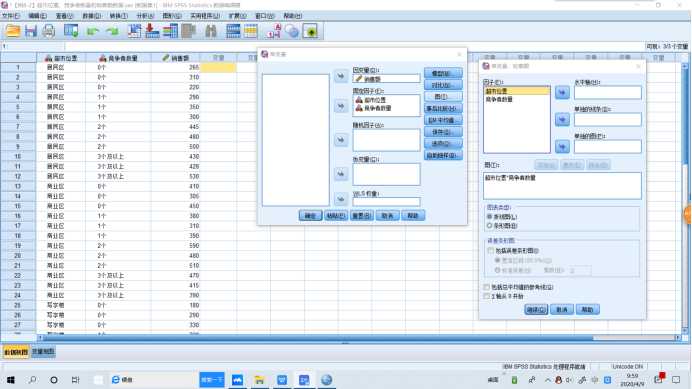
　　SPSS操作：【分析】→【一般线性模型-单变量】，将因变量选入【因变量】，将自变量选入【固定因子】。如果需要均值图示，【绘图】，将因子选入【水平轴】，【图】→【添加】。如果需要多重比较时，【事后多重比较】，将因子选入【两两比较检验】，【假定方差齐性】→【LSD】。如果需要相关统计量时，【选项】→【显示】→【描述统计量】。如果需要方差齐性检验时，【选项】→【输出】→【齐性检验】。如果需要对模型的参数进行估计时，【选项】→【输出】→【参数估计值】。如果需要预测值时，【保存】→【预测值】→【未标准化】。

　　

 

　　

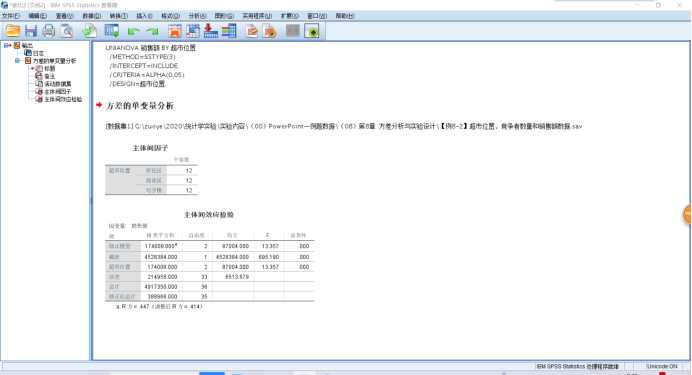
1 UNIANOVA 销售额 BY 超市位置
2   /METHOD=SSTYPE(3)
3   /INTERCEPT=INCLUDE
4   /CRITERIA=ALPHA(0.05)
5   /DESIGN=超市位置.

方差单变量分析1

　　

 

　　

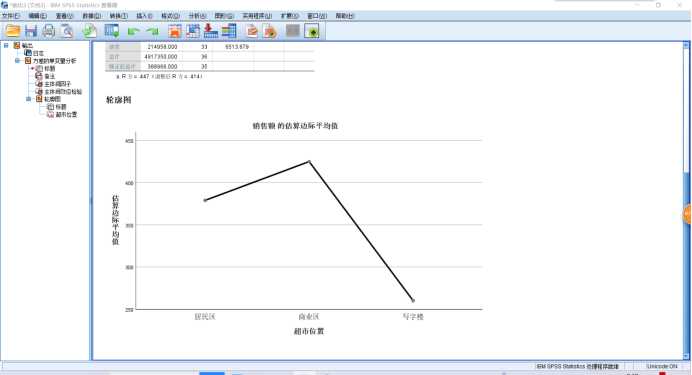
1 UNIANOVA 销售额 BY 超市位置
2   /METHOD=SSTYPE(3)
3   /INTERCEPT=INCLUDE
4   /PLOT=PROFILE(超市位置) TYPE=LINE ERRORBAR=NO MEANREFERENCE=NO YAXIS=AUTO
5   /CRITERIA=ALPHA(0.05)
6   /DESIGN=超市位置.

单因数方差分析2轮廓图

　　

 

　　

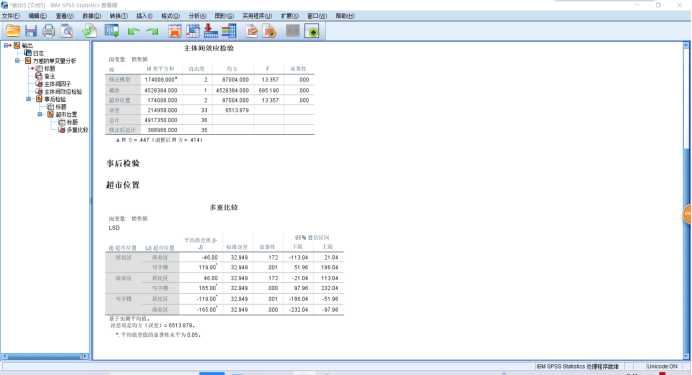
1 UNIANOVA 销售额 BY 超市位置
2   /METHOD=SSTYPE(3)
3   /INTERCEPT=INCLUDE
4   /POSTHOC=超市位置(LSD)
5   /CRITERIA=ALPHA(0.05)
6   /DESIGN=超市位置.

单因数方差分析3

　　

 

　　

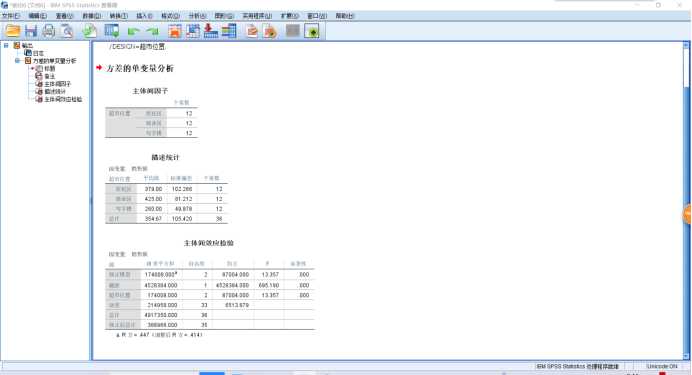
1 UNIANOVA 销售额 BY 超市位置
2   /METHOD=SSTYPE(3)
3   /INTERCEPT=INCLUDE
4   /PRINT DESCRIPTIVE
5   /CRITERIA=ALPHA(.05)
6   /DESIGN=超市位置.

单因数方差分析4

　　

 

 

 　　

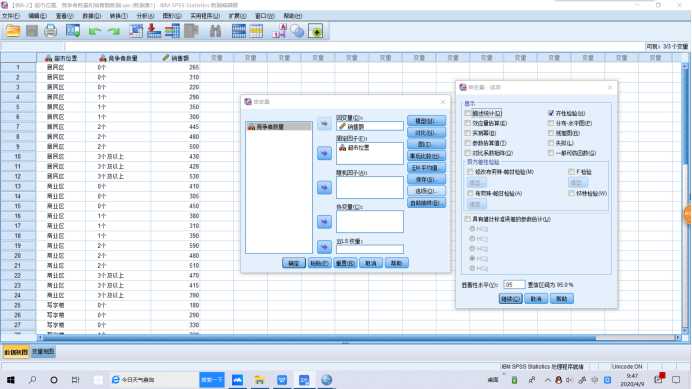
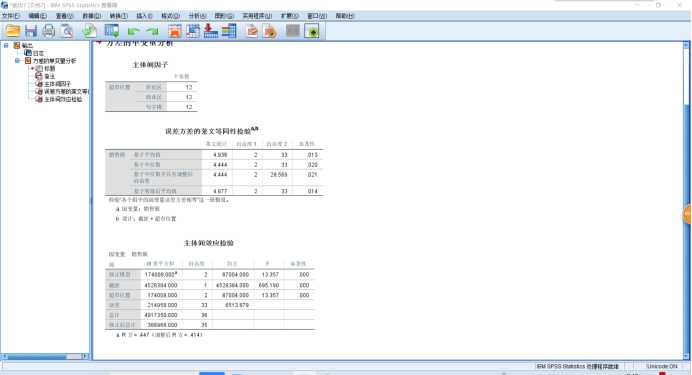
1 UNIANOVA 销售额 BY 超市位置
2   /METHOD=SSTYPE(3)
3   /INTERCEPT=INCLUDE
4   /PRINT HOMOGENEITY
5   /CRITERIA=ALPHA(.05)
6   /DESIGN=超市位置.

单因数方差分析5

　　

 

　　

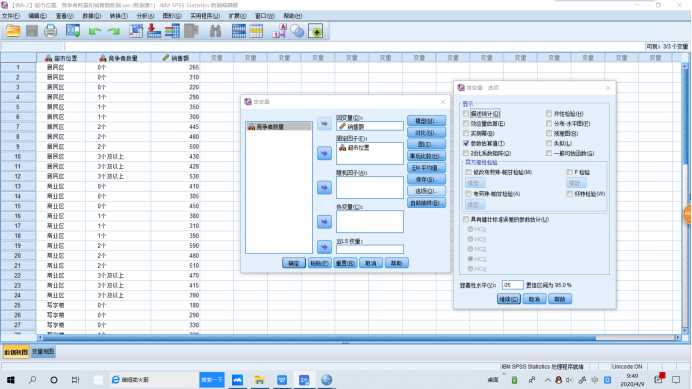
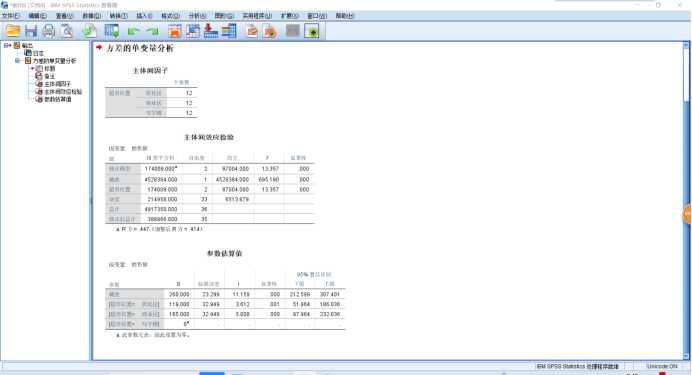
1 UNIANOVA 销售额 BY 超市位置
2   /METHOD=SSTYPE(3)
3   /INTERCEPT=INCLUDE
4   /PRINT PARAMETER
5   /CRITERIA=ALPHA(.05)
6   /DESIGN=超市位置.

单因数方差分析6

　　

 

 

 　　

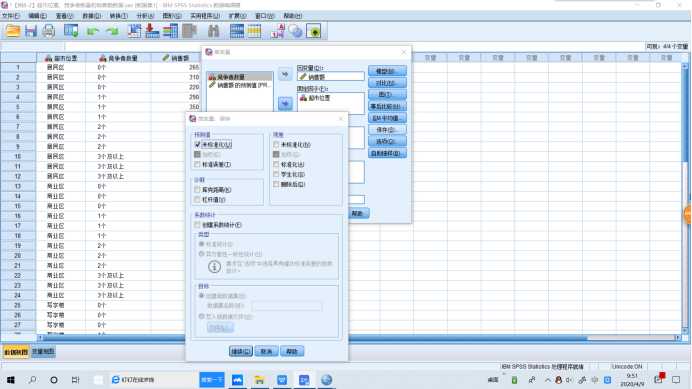
1 UNIANOVA 销售额 BY 超市位置
2   /METHOD=SSTYPE(3)
3   /INTERCEPT=INCLUDE
4   /SAVE=PRED
5   /CRITERIA=ALPHA(.05)
6   /DESIGN=超市位置.

单因数方差分析7

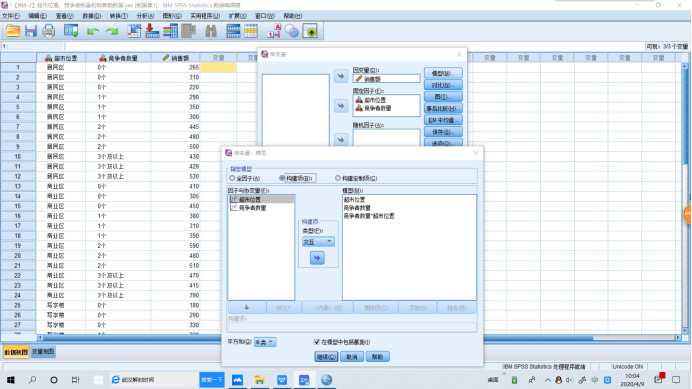
　　2.双因数方差分析：分析两个因数对实验结果的影响。可以根据两个因数间对实验结果的影响大致分为两类，当2个因素对实验数据单独影响时，只考虑主效应的双因数方差分析；当因数2个因数对实验数据的单独影响外，两因数的搭配还会对结果产生一种新的影响，这时考虑交互效应的双因数方差分析。

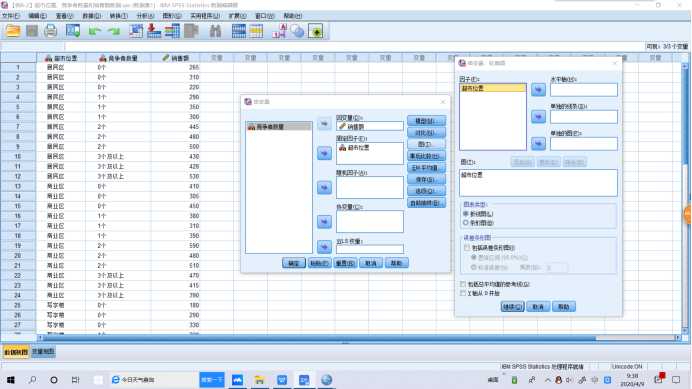
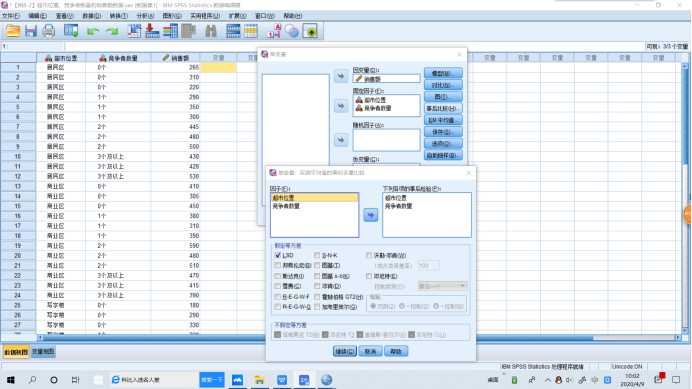
　　SPSS操作：需要均值图示，【图】，将因子A选入【水平轴】，将因子B选入【单独的线条】，【图】→【添加】。需要多重比较时，【事后多重比较】，将因子A，B选入【两两比较检验】→【假定方差齐性】→【LSD】。需要分析交互效应时，【分析】→【一般线性模型-单变量】，将因变量选入【因变量】，将自变量选入【固定因子】→【模型】→【定制】，将因子A，B选入【模型】（将因子A，B选入【模型】按shift）→【构建项】→【交互】。

　　

 

 　　

 

 　　

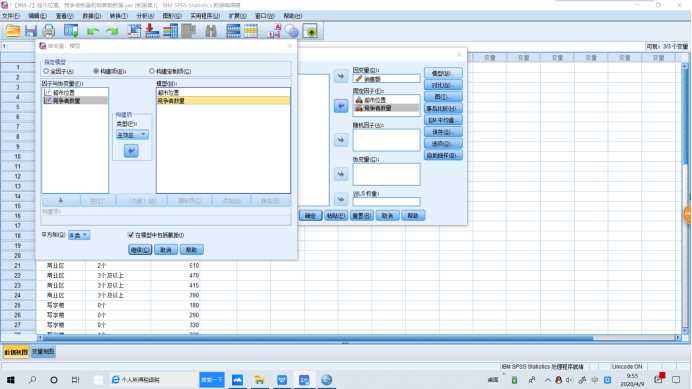
主体间效应检验
因变量:   销售额
源	III 类平方和	自由度	均方	F	显著性
修正模型	282670.222a	5	56534.044	15.956	.000
截距	4528384.000	1	4528384.000	1278.052	.000
超市位置	174008.000	2	87004.000	24.555	.000
竞争者数量	108662.222	3	36220.741	10.223	.000
误差	106295.778	30	3543.193
总计	4917350.000	36
修正后总计	388966.000	35
a. R 方 = .727（调整后 R 方 = .681）

　　

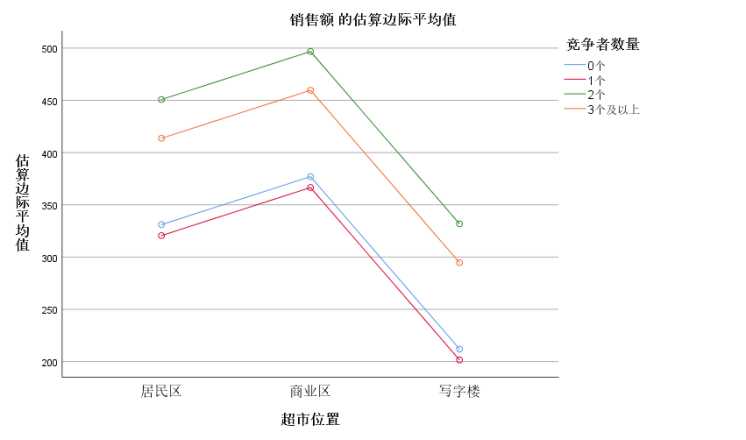
1 UNIANOVA 销售额 BY 超市位置 竞争者数量
2   /METHOD=SSTYPE(3)
3   /INTERCEPT=INCLUDE
4   /PLOT=PROFILE(超市位置*竞争者数量) TYPE=LINE ERRORBAR=NO MEANREFERENCE=NO YAXIS=AUTO
5   /CRITERIA=ALPHA(.05)
6   /DESIGN=超市位置 竞争者数量.

双因数方差分析1

　　

 

多重比较
因变量:   销售额
LSD
(I) 竞争者数量	(J) 竞争者数量	平均值差值 (I-J)	标准误差	显著性	95% 置信区间
					下限	上限
0个	1个	10.44	28.060	.712	-46.86	67.75
	2个	-119.78*	28.060	.000	-177.08	-62.47
	3个及以上	-82.67*	28.060	.006	-139.97	-25.36
1个	0个	-10.44	28.060	.712	-67.75	46.86
	2个	-130.22*	28.060	.000	-187.53	-72.92
	3个及以上	-93.11*	28.060	.002	-150.42	-35.80
2个	0个	119.78*	28.060	.000	62.47	177.08
	1个	130.22*	28.060	.000	72.92	187.53
	3个及以上	37.11	28.060	.196	-20.20	94.42
3个及以上	0个	82.67*	28.060	.006	25.36	139.97
	1个	93.11*	28.060	.002	35.80	150.42
	2个	-37.11	28.060	.196	-94.42	20.20
基于实测平均值。  误差项是均方（误差）= 3543.193。
*. 平均值差值的显著性水平为 .05。

 

1 UNIANOVA 销售额 BY 超市位置 竞争者数量
2   /METHOD=SSTYPE(3)
3   /INTERCEPT=INCLUDE
4   /POSTHOC=超市位置 竞争者数量(LSD)
5   /CRITERIA=ALPHA(.05)
6   /DESIGN=超市位置 竞争者数量.

双因数方差分析2

　　

 

主体间效应检验
因变量:   销售额
源	III 类平方和	自由度	均方	F	显著性
修正模型	330592.667a	11	30053.879	12.357	.000
截距	4528384.000	1	4528384.000	1861.830	.000
超市位置	174008.000	2	87004.000	35.771	.000
竞争者数量	108662.222	3	36220.741	14.892	.000
超市位置 * 竞争者数量	47922.444	6	7987.074	3.284	.017
误差	58373.333	24	2432.222
总计	4917350.000	36
修正后总计	388966.000	35
a. R 方 = .850（调整后 R 方 = .781）

 

1 UNIANOVA 销售额 BY 超市位置 竞争者数量
2   /METHOD=SSTYPE(3)
3   /INTERCEPT=INCLUDE
4   /CRITERIA=ALPHA(.05)
5   /DESIGN=超市位置 竞争者数量 竞争者数量*超市位置.

双因数方差分析3

 

小结：

　　注意要求做分析。