平衡树

Posted 2021-02-20 sktskyking

前置知识

二叉搜索树：

1. 显然是一棵二叉树,

2. 每个节点有一个权值val,

3. 对于每个节点k,要么其左子树为空,否则其左子树的所有元素节点权值都小于val[k],

   对于其右子树,要求其中权值全部大于val[k],

4. 如果整棵树中有几个节点权值相等,那么将这个元素对应的节点多开一个域sum,表示这个权值的元素的个数

5. 树中所有子树全是BST（对于任意的node x，如果node y是node x的左边的节点, 那么Key(y) <= Key(x); 对于任意的node x，如果node y 是node x的右边的节点，那么key(y)>=key(x).）

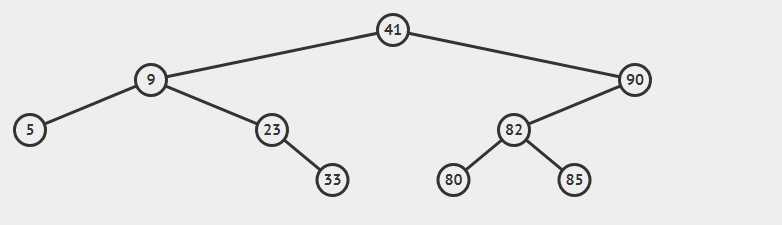
这样一个建立结构的规则非常适合数的查找,基本上就是二分的思路,无论是访问第k小值,还是访问权值为v的节点,都可以快速地实现目标,插入也是如此

具体步骤(比如找权值为v的元素):

1. 从根节点开始寻找:

2. 对于当前节点k,如果现在v=val[k],

3. 否则,如果当前值较小,说明目标值一定在左子树,查找左儿子,否则去查找右儿子,

4. 重复2-3步,直到出现以下两种状况:

   • 在查找过程中如步骤2,找到节点,完成查找,

   • 直到找到最下方的空节点,也没有找到目标节点,说明这个节点并不存在

     (查询操作一般不会这样的)

     p.s. 对于插入操作,如果找到第二种情况的空节点,那么说明可以直接插入这个新节点

JYY说：这里注意,我们处理这些信息根本不用递归,只需要写个函数然后在函数之内跑循环就完了,这样更加高效。可以发现这样类似于二分的方法是非常高效的,可以方便地维护出数列中与大小关系有关的数据

比如说:

• 求第k大的数的值

• 求大小为v的元素的排名

• 求比v大的最小数(后继)

• 求比v小的最大数(前驱)

注意区间求值是树套树的操作,不是BST的操作

完全不需要Splay的一些操作及函数实现:

所需变量

int ch[N][2],f[N],size[N],sum[N],val[N];
int rt,cnt;

一般采用动态开点的操作来进行元素插入(随开随用）

这里变量cnt就是这样一个作用,开点的时候:

	++cnt;
	nd[cnt]=...;

rt存的是当前BST的根

ch[k][0/1]储存的是每个节点的左右儿子,ch[k][0]为左,ch[k][1]为右,

f[k]储存的则是节点父亲f[rt]=0,

val[k]存的是k节点的值,

size[k]存以节点k为根的子树的大小,

sum[k]存元素k出现的次数,就是序列中有几个值为val[k]的元素

更新函数update

用于更新节点信息,具体作用其实就是维护子树大小,节点的关系不改变

inline void update(ci x){
    if(!x) return ;
    size[x]=sum[x];
    if(ch[x][0]) size[x]+=size[ch[x][0]];
    if(ch[x][1]) size[x]+=size[ch[x][1]];
}

 

翻译:

• 空节点放弃
• 否则先将当前子树大小赋值为当前元素个数
• 如果有左儿子就加上左儿子的子树大小,右儿子同理

这里注意这个函数的使用,update操作一定要先对子节点再对父节点,这样才能保证正确性,

因为越是深度小的节点,其信息就越是从子节点合并上来的,如果先更新父节点,父节点的信息很可能没有被"最新"子节点信息更新,反而被未更新的"老"子节点更新,在信息访问的时候会爆炸,实为下策

如果先维护子节点,那么其所有祖宗节点的更新都有了保障,因为其使用的子节点信息全部是更新过的,

插入函数insert

代码给出,

inline void insert(ci x){
    if(!rt){
        cnt++;
        ch[cnt][0]=ch[cnt][1]=f[cnt]=0;
        rt=cnt;
        size[cnt]=sum[cnt]=1;
        val[cnt]=x;
        return ;
    }int now=rt,fa=0;
    while(1){
        if(val[now]==x){
            sum[now]++;
            update(now);
            update(fa);
            return ;
        }fa=now;
        now=ch[now][val[now]<x];
        if(!now){
            cnt++;
            ch[cnt][0]=ch[cnt][1]=0;
            f[cnt]=fa;
            sum[cnt]=size[cnt]=1;
            ch[fa][val[fa]<x]=cnt;
            val[cnt]=x;
            update(fa);
            return ;
        }
    }
}

 

• 连根都每有就是空树,直接建点返回(具体建点操作不解释)
• 否则,开始查找插入元素应该在的位置,寻找规律同最上面介绍的步骤
  • 如果已有元素,就直接把元素个数更新,再依次把当前节点和其父节点元素进行更新,不用再管其他节点
  • 否则,新建节点并维护好父子关系,更新父节点信息,并没有必要更新自己

上面讲到,每个非叶节点的子树大小都是由子节点维护上来的,那么只要子节点是新的,父节点的维护就一定不会出错,只是时间可能晚一些

也就是说,对于操作更新的子树大小的信息,我们完全可以将离当前节点很远的祖宗节点暂时放弃修改,等着以后在遍历到这个节点是顺便进行更新,既不会导致错误,也提升了代码效率,

但前提就是先维护子节点

找v函数find

就是模拟,找小往左找大往右,

inline int find(ci x){
    int k=0,now=rt;
    while(1){
        if(x<val[now]) now=ch[now][0];
        else{
            k+=(ch[now][0]?size[ch[now][0]]:0);
            if(val[now]==x) return k+1;
            k+=sum[now];
            now=ch[now][1];
        }
    }
}

 

注意处理好儿子的存在性问题

找第k小元素 find_kth

inline int find_kth(int x){
    int now=rt;
    while(1){
        if(ch[now][0]&&x<=size[ch[now][0]])
            now=ch[now][0];
        else{
            int temp=(ch[now][0]?size[ch[now][0]]:0)+sum[now];
            if(x<=temp) return val[now];
            x-=temp;
            now=ch[now][1];
        }
    }
}

 

对于当前子树,要找第k小元素

从左子树找,就从左子树找其中的k小元素,从右子树找就找右子树中的第k−size[左儿子]小的元素

因为只要在右子树中寻找,这个元素就一定是大于左子树中所有元素的,其元素排名一定是大于左子树大小的

求前驱/后继

就是查询比某个数小的最大数,或是比其大的最小数,

要知道的就只是个思路就行,主要就是先找目标元素对应的节点,如果查前驱就往左边找,找左边最靠右的

(这里不一定是左子树,万一要查询的元素是叶节点呢)

查后继就往右边找,同理不再赘述,

//加上某种操作,让查询的元素成为根(不存在就先插入,完成查询再删除)...val[rt]存的即为查询的值
inline int pre(){
    int now=ch[rt][0];
    while(ch[now][1]) now=ch[now][1];
    return now;
}
inline int next(){
    int now=ch[rt][1];
    while(ch[now][0]) now=ch[now][0];
    return now;
}

 

对于删除操作,因为BST虽是可以实现,但是实现方法与下面要讲的Splay删除相比,并不精彩,

到此前置知识部分结束

Splay的意义

作为一棵平衡树,Splay显然也是一棵BST,但是显然有不同,

Splay等平衡树是基于BST的优化

考虑BST有什么可以优化的:

• 众所周知,BST用的是二分的相关思想,所维护的节点关系就只有"左小右大"

  因为只维护一个性质,所以其结构并不唯一,

  比如下面的这棵BST

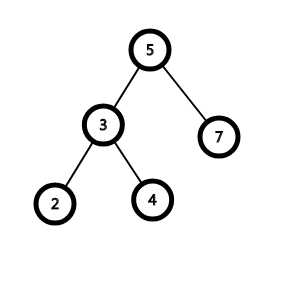
显然也可以是这样:

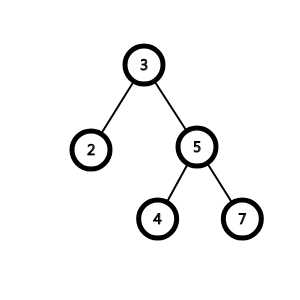
所以,但凡数据有序,就会这样:

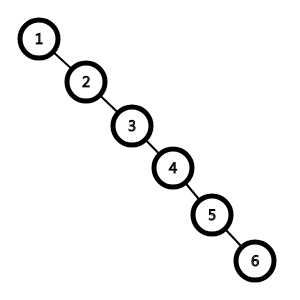
也就是说,原本可以二分的树现在变成了一条链,只能O(n2)暴力,大大降低效率

这样一来,树的形态似乎完全取决于插入的顺序,数据又取决于人...

树的形态又决定了代码的效率,因为我们知道一棵树中一定是拥有两个子节点的节点个数越多越好,

这样才能高效地二分,

对于链(或者结构凡是像链),就只能暴力查找,失去了BST原本的优良性质

这时就需要SPLAY

操作及原理

Splay的汉语释义是"伸展",显然,我们不能一巴掌把一棵BST物理伸展开来,

我们考虑旋转操作,

就是我们通过花式旋转,把BST伸展,

先看看怎么旋转,再去看怎么通过新定义的旋转实现树的伸展,

旋转操作x我们现在“发明”一个函数,传唯一的参数x,表示让节点x旋转到其父亲的位置,当然树的结构改变,但是树作为BST的性质没有改变,

我们根据实际情况来判断到底如何实现

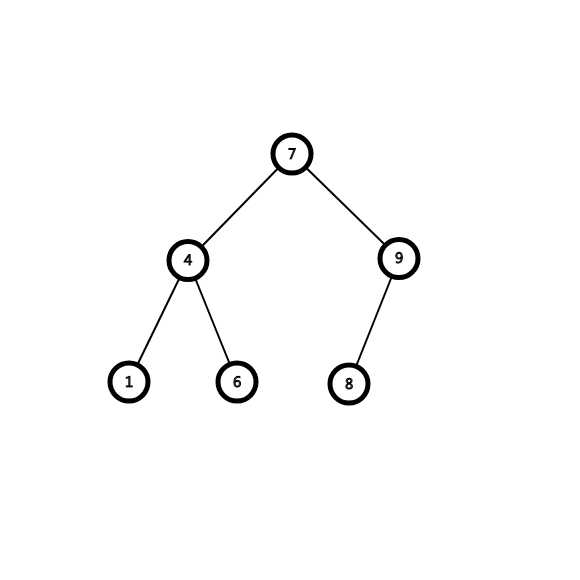
加入我们要让节点4旋转到其父亲位置-7的位置上去,

在旋转的同时,我们需要考虑节点关系的过继问题,

考虑下面几种策略:

• 直接让节点4到节点7的位置上去,
• 因为节点4的整棵右子树一定在节点7的左子树里面,说明都比7小,那么把节点7合并到节点4的右子树中去,如果右子树的右子树中还有比7小的元素,就继续递归,直到节点7连到子树上
• 这时我们发现节点7的整棵右子树不变,直接做了节点4的第n棵右子树

按照这种思路维护出来是这样:

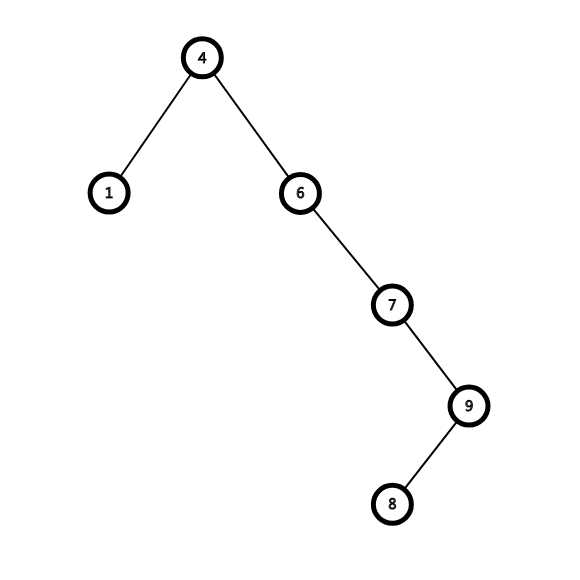
直接变成链...

如果这样操作的话,节点4的位置倒是很好操作,但是其子树中的节点关系不好维护,如果将节点7归到节点6的右子树中去,实在难有结论,

不难看出这种情况就算很优秀,其子树中关系维护也真的不好写,

同时我们发现,上面这种维护实质确实是"伸展"了这棵BST,但是这种操作实际上是把树往链的方向展开,

因为在旋转的同时,我们只是将4节点的位置进行调换,将其它节点关系丢给子树去处理,这使得本来就属于节点4的子树和节点7及其整棵右子树一起为树的高度贡献了不可或缺的力量...

这里原本节点7的左子树是节点4为根的树,但是旋转以后我们发现节点7的左子树根本不见了,因为我根本没有考虑节点7的左子树这个空间该怎么去用,导致了树中位置的浪费,进而导致链的形成

一开始我们就提到,链的形态是并不利于BST操作的,所以这种方法并不可取,

我们所说的"Splay伸展"是为了尽量减少树的高度,为了维护其BST操作较方便的形态,

我们不妨考虑这样的方法:

• 我们发现节点6为根的整棵树(在这里是节点6本身)一定比节点4大,比节点7小,
• 那么我考虑用上刚刚提到的节点7的左子树空间,鉴于其值大小合适,我们可以将"节点6根"树整棵地作为节点7的新左子树,毕竟转完了节点7的右边也寂寞的很...
• 然后将"节点7根"树整棵作为节点4的右子树存下
• 上面是对于特定情况,我们概括一下
• 对于当前节点,将自己的右子树过继给父节点,当做父节点的左子树,然后将以父节点为根的整棵树作为当前节点的右子树,就完成了旋转操作,

维护完像这样:

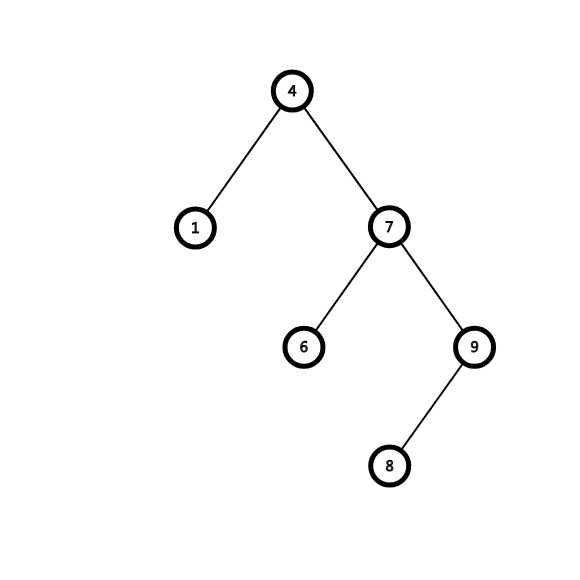
这样一来显然这棵树显得满多了,起码比之前链的形态好很多,

然而上面概括的步骤仅是对于当前节点是父节点的左儿子的情况,

同理,对于右边的节点要旋转到其父亲的位置,只需要把目标节点的左子树接到父节点的右子树上,再将父节点的整棵树接到目标节点的左子树就好了

于是我们有了旋转操作的思想的思想

真正的旋转-rotate

有了上面的思路,只需要写并不繁琐的模拟代码就可以实现辣!

先写下get函数,判断目标节点是哪个儿子

inline int get(ci x){
    return ch[f[x]][1]==x;
}

inline void rotate(ci x){
    int old_root=f[x],old_fa=f[f[x]],opr=get(x);
    ch[old_root][opr]=ch[x][opr^1];
    f[ch[old_root][opr]]=old_root;
    ch[x][opr^1]=old_root;
    f[old_root]=x;
    f[x]=old_fa;
    if(old_fa) ch[old_fa][ch[old_fa][1]==old_root]=x;
    update(old_root);
    update(x);
}

因为在处理节点关系的时候会非常乱,所以先开变量储存原来节点的关系,就是存一下原来谁是爹,谁是爷爷什么的...

最后进行更新,还是依据儿子优先法则

不得不说一句,Tarjan大佬发明的数据结构操作就是强,连儿子身份的判断与运算也这样简洁,来去自如!

伸展操作splay

我们知道一个非根节点,它不是左儿子就是右儿子

那么我们规定,这个"左儿子","右儿子"这些称呼叫做这个节点的身份

这里的splay指的就是伸展函数了,目的就是伸展,但是其主要目的是把目标节点旋转到根节点

而且在Splay中,几乎处处可见splay函数的身影,就是因为Splay实在频繁的更新结构的状态下维护形态的优美的

具体思路:

如果我们要让最底部的节点升到根节点位置,

考虑现在有一条链(当然在Splay里因为频繁维护并不会出现长度非常长的链的情况):

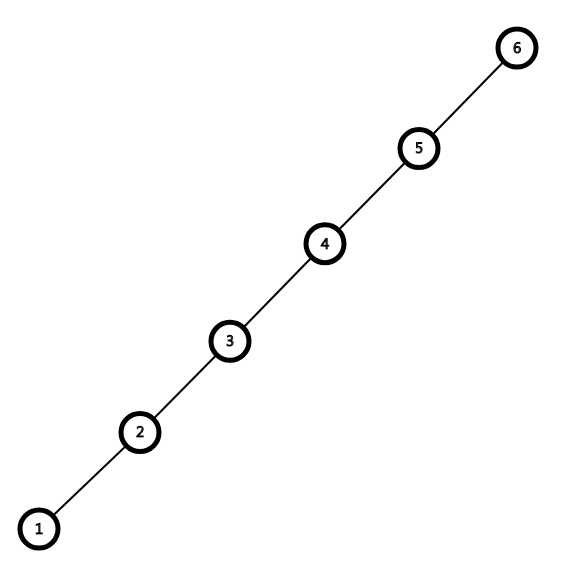
我们要让BST维护树的优美性质,显然我们需要让BST盘区折叠,现在我们要splay节点1旋转到根节点的位置,

在旋转之前,我们先思考一下,如何转才能让BST有一个多叉的结构,

不难看出,"多叉"转化为图中的信息,就是节点的儿子尽可能的多,

但是如果我们仅以将节点1旋转为根节点为目的,这样旋转:

while(rt!=1){
	rotate(1);
}

旋转完成后

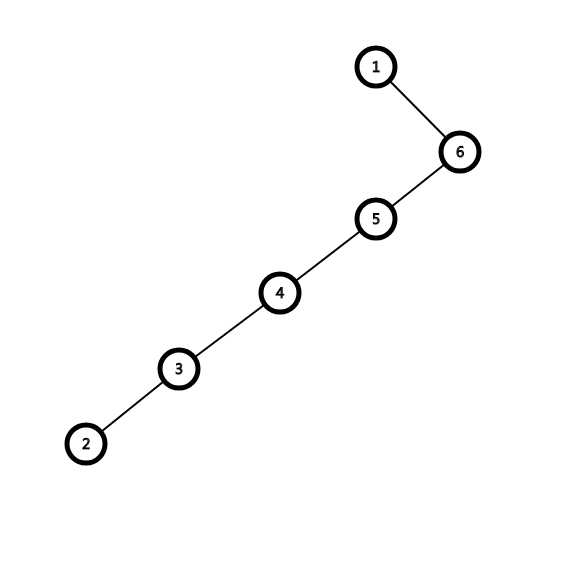
,如果这样那splay的工作就仅是调整了节点的位置,并没有对结构进行优化

那么为了使树的就够更加盘区折叠,我们这样操作:

对于当前节点,如果其身份和其父节点的身份不一致,说明这棵树本身就比较优美,可以直接对当前节点进行rotate

如果其节点身份同其父节点身份相同,那么我们起码可以判断我们要操作的节点似乎形成了一个链状结构,

那么为了破坏这个链状结构,使其结构弯曲,

我们先对目标节点的父亲进行rotate,这样就破坏了链的结构,

然后再对目标节点进行rotate,

重复以上步骤直到目标节点为根节点.

伸展完成后:

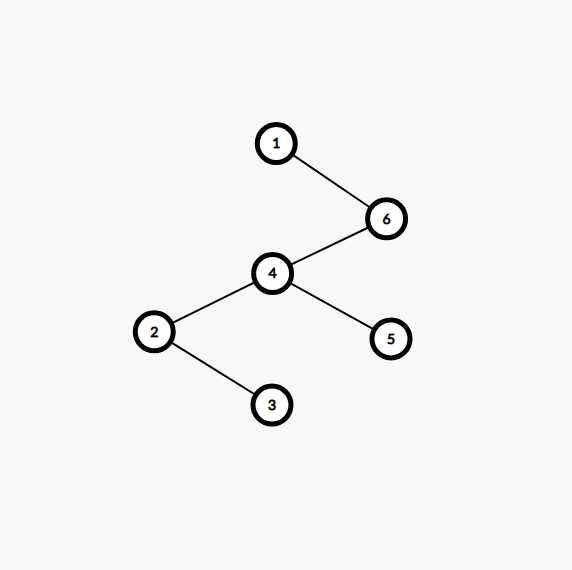
这样一来就好多了,

于是以上法则就是我们伸展BST的法则,然后自己模拟下

当然建议自己多举几个例子找普遍规律.

代码

inline void splay(int x){
    for(int fa;fa=f[x];rotate(x))
        if(f[fa])
            rotate((get(x)==get(fa))?fa:x);
    rt=x;
}

 

这里for循环中fa=f[x]的用法是先赋值再判断,判断fa是否为0(节点的父亲是否存在)

于是,基于此,几乎所有函数我么都可以加一条splay函数,让当前操作的目标旋转为根节点,一来方便操作,二来优化了结构

Splay删除操作

这里指的删除指的不一定是元素删除,更多的是元素个数-1,元素消失只是元素个数为0这一特殊情况

当然前提是找到元素x,我们可以顺便将其旋转到根节点,以便操作,

也就是说我们操作的时候,目标节点已经是根节点了,

然后暴力分情况讨论:

1. 元素个数不为1,直接将元素个数-1后更新节点信息完

2. 如果个数为1,但是左右儿子都为空的话,也就是说,删除操作之后,整棵树就会变为空树,那么直接清零就行了,此时rt=0

3. 如果个数为1,且只有一个儿子的话,显然自己删掉以后将儿子赋为根就好了

4. 否则,就是最普遍的情况,

   当前节点删了就没,而且还同时拥有左右儿子,这使得删除操作很难受,

   我们采取暴力而简洁的方法:

   把目标节点的前缀旋转做根,这个操作使得前缀与目标节点直接相连,同时前缀节点就是根节点了,此时目标节点一定是这棵树根节点的右儿子,

   这样我们可以直接将目标节点删除以后,将目标节点的右儿子提上来当做根节点的右儿子,这样一来目标节点就没了

代码:

inline void del(ci x){
    find(x); //其中含有splay操作,将目标节点转移到根的位置
    if(sum[rt]>1){sum[rt]--;update(rt);return ;}
    if(!ch[rt][0]&&!ch[rt][1]){clear(rt);rt=0;return ;}
    if(!ch[rt][0]){
        int old_root=rt;
        rt=ch[rt][1];
        f[rt]=0;
        clear(old_root);
        return ;
    }
    if(!ch[rt][1]){
        int old_root=rt;
        rt=ch[rt][0];
        f[rt]=0;    
        clear(old_root);
        return ;
    }
    int prev=pre(),old_root=rt;
    splay(prev);
    ch[rt][1]=ch[old_root][1];
    f[ch[old_root][1]]=rt;
    clear(old_root);
    update(rt);
}

 

同样需要保存原先节点的关系

以上就是所有Splay的操作函数

Splay总代码

#include<iostream>
#include<cstdio>
#define ci const int &
using namespace std;
const int N=100005;
int n;
int ch[N][2],f[N],size[N],sum[N],val[N];
int rt,cnt;
inline void clear(ci x){
    ch[x][0]=ch[x][1]=f[x]=val[x]=sum[x]=size[x]=0;
}
inline int get(ci x){
    return ch[f[x]][1]==x;
}
inline void update(ci x){
    if(!x) return ;
    size[x]=sum[x];
    if(ch[x][0]) size[x]+=size[ch[x][0]];
    if(ch[x][1]) size[x]+=size[ch[x][1]];
}
inline void rotate(ci x){
    int old_root=f[x],old_fa=f[f[x]],opr=get(x);
    ch[old_root][opr]=ch[x][opr^1];
    f[ch[old_root][opr]]=old_root;
    ch[x][opr^1]=old_root;
    f[old_root]=x;
    f[x]=old_fa;
    if(old_fa) ch[old_fa][ch[old_fa][1]==old_root]=x;
    update(old_root);
    update(x);
}
inline void splay(int x){
    for(int fa;fa=f[x];rotate(x))
        if(f[fa])
            rotate((get(x)==get(fa))?fa:x);
    rt=x;
}
inline void insert(ci x){
    if(rt==0){
        cnt++;
        ch[cnt][0]=ch[cnt][1]=f[cnt]=0;
        rt=cnt;
        size[cnt]=sum[cnt]=1;
        val[cnt]=x;
        return ;
    }int now=rt,fa=0;
    while(1){
        if(val[now]==x){
            sum[now]++;
            update(now);
            update(fa);
            splay(now);
            return ;
        }fa=now;
        now=ch[now][val[now]<x];
        if(now==0){
            cnt++;
            ch[cnt][0]=ch[cnt][1]=0;
            f[cnt]=fa;
            sum[cnt]=size[cnt]=1;
            ch[fa][val[fa]<x]=cnt;
            val[cnt]=x;
            update(fa);
            splay(cnt);
            return ;
        }
    }
}
inline int find(ci x){
    int k=0,now=rt;
    while(1){
        if(x<val[now]) now=ch[now][0];
        else{
            k+=(ch[now][0]?size[ch[now][0]]:0);
            if(val[now]==x){splay(now);return k+1;}
            k+=sum[now];
            now=ch[now][1];
        }
    }
}
inline int find_kth(int x){
    int now=rt;
    while(1){
        if(ch[now][0]&&x<=size[ch[now][0]])
            now=ch[now][0];
        else{
            int temp=(ch[now][0]?size[ch[now][0]]:0)+sum[now];
            if(x<=temp) return val[now];
            x-=temp;
            now=ch[now][1];
        }
    }
}
inline int pre(){
    int now=ch[rt][0];
    while(ch[now][1]) now=ch[now][1];
    return now;
}
inline int next(){
    int now=ch[rt][1];
    while(ch[now][0]) now=ch[now][0];
    return now;
}
inline void del(ci x){
    find(x);
    if(sum[rt]>1){sum[rt]--;update(rt);return ;}
    if(!ch[rt][0]&&!ch[rt][1]){clear(rt);rt=0;return ;}
    if(!ch[rt][0]){
        int old_root=rt;
        rt=ch[rt][1];
        f[rt]=0;
        clear(old_root);
        return ;
    }
    if(!ch[rt][1]){
        int old_root=rt;
        rt=ch[rt][0];
        f[rt]=0;    
        clear(old_root);
        return ;
    }
    int prev=pre(),old_root=rt;
    splay(prev);
    ch[rt][1]=ch[old_root][1];
    f[ch[old_root][1]]=rt;
    clear(old_root);
    update(rt);
}
int main(){
    scanf("%d",&n);
    while(n--){
        int opr,x;
        scanf("%d%d",&opr,&x);
        if(opr==1) insert(x);
        if(opr==2) del(x);
        if(opr==3) printf("%d
",find(x));
        if(opr==4) printf("%d
",find_kth(x));
        if(opr==5){insert(x);printf("%d
",val[pre()]);del(x);}
        if(opr==6){insert(x);printf("%d
",val[next()]);del(x);}
    }return 0;
}

最后：jyyNB!