「SPOJ DYNALCA」Dynamic LCA

Posted 2021-02-20 -wallace-

Description

有一个森林最初由 (n) 个互不相连的点构成

你需要处理以下 (m) 次操作：

link A B：添加从顶点A到B的边，使 (A) 成为 (B) 的子节点，其中保证 (A) 是一个根顶点，(A) 和 (B) 在不同的树中。

cut A：切断点 (A) 到其父节点的边，保证 (A) 是一个非根节点。

lca A B：输出 (A) 和 (B) 的最近共同祖先，保证 (A) 和 (B) 在同一棵树中。

Hint

(1le n, mle 10^5)

Solution

看到加边和删边，不难想到用 ( exttt{Link-Cut Tree})。

但难点在于求 LCA。

假设我们有这样一颗树，以 1 为根，并要求 lca 6 9：

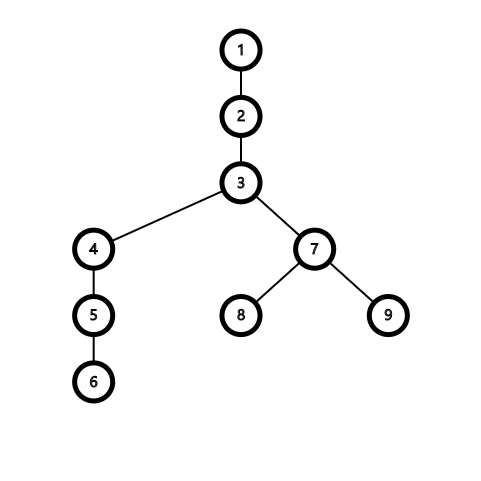
先打通 6 到 根 的实链（红色边为实边），access(6)：

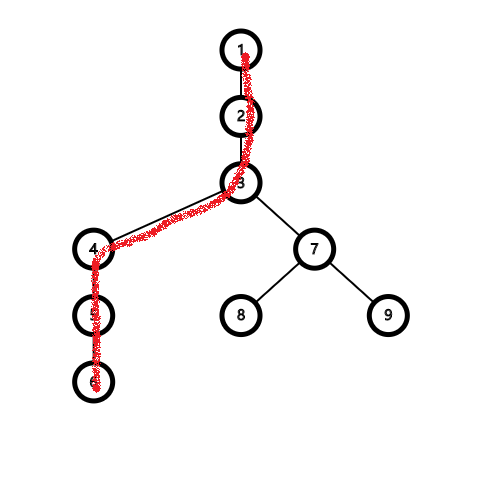
如果我们再 access(9)，那么：

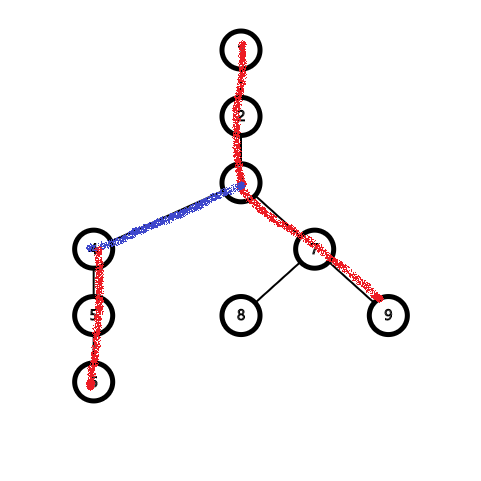
可以发现，原来有一条实边变虚（蓝色边）了，而这条虚边的父结点正是所求的最近公共祖先。

结论，access(x) 后，再 access(y) 的过程中实变虚的最后一条边就是 LCA(x, y)。

具体做法，可以在 access 函数中加入返回值会好做一些。

inline int access(int x) {
	register int y = 0;
	for (; x; x = fa[y = x]) splay(x), rc = y;
	return y;
}
inline int LCA(int x, int y) {
	return access(x), access(y);
}

注意，cut 操作不能 makrRoot，因为 LCA 这个东西是会受根结点的位置影响的，不可随意换根。而 link 由于 (x) 本来就是根，makeRoot 没有关系。

Code

#include <iostream>
#include <string>

using namespace std;
const int N = 1e5 + 5;

int ch[N][2], fa[N];
bool rev[N];

#define lc ch[x][0]
#define rc ch[x][1]

inline bool isRoot(int x) {
	return x != ch[fa[x]][0] && x != ch[fa[x]][1];
}
inline int getc(int x) {
	return x == ch[fa[x]][1];
}

inline void setRev(int x) {
	swap(lc, rc), rev[x] ^= 1;
}
inline void pushdown(int x) {
	if (rev[x]) {
		if (lc) setRev(lc);
		if (rc) setRev(rc);
		rev[x] = 0;
	}
}
inline void pushdownAll(int x) {
	if (!isRoot(x)) pushdownAll(fa[x]);
	pushdown(x);
}

inline void rotate(int x) {
	int y = fa[x], z = fa[y];
	int k = getc(x), w = ch[x][!k];
	if (!isRoot(y)) ch[z][getc(y)] = x;
	ch[x][!k] = y, ch[y][k] = w;
	if (w) fa[w] = y;
	fa[y] = x, fa[x] = z;
}
inline void splay(int x) {
	pushdownAll(x);
	for (register int y = fa[x]; !isRoot(x); rotate(x), y = fa[x])
		if (!isRoot(y)) rotate(getc(x) != getc(y) ? x : y);
}

inline int access(int x) {
	register int y = 0;
	for (; x; x = fa[y = x]) splay(x), rc = y;
	return y;
}
inline void makeRoot(int x) {
	access(x), splay(x), setRev(x);
}
inline void link(int c, int f) {
	makeRoot(c), fa[c] = f;
}
inline void cut(int x) {
	access(x), splay(x), fa[lc] = 0, lc = 0;
}
inline int LCA(int x, int y) {
	return access(x), access(y);
}

signed main() {
	int n, q;
	ios::sync_with_stdio(false);
	cin >> n >> q;
	
	for (; q; --q) {
		string cmd; int x, y;
		cin >> cmd;
		
		if (cmd == "lca")
			cin >> x >> y, cout << LCA(x, y) << endl;
		if (cmd == "link")
			cin >> x >> y, link(x, y);
		if (cmd == "cut")
			cin >> x, cut(x);
	}
	return 0;
}