教你用神经网络求解高级数学方程！

Posted 2021-02-20 jinsexiaomifeng

　　教你用神经网络求解高级数学方程！

　　本文介绍了一种利用深度学习中的神经机器翻译（NMT）技术求解方程问题的方法和系统，该系统展示了深度学习应用在更广泛领域的潜力。

　　Facebook AI建立了第一个可以使用符号推理解决高级数学方程的AI系统。通过开发一种将复杂数学表达式表示为一种语言的新方法，然后将解决方案视为序列到序列的神经网络的翻译问题，我们构建了一个在解决积分问题以及一阶和二阶微分方程方面都优于传统计算系统的系统。

　　以前，这类问题被认为是深度学习模型所无法企及的，因为求解复杂方程需要精度而不是近似值。神经网络擅长通过近似达到成功，例如认识像素的特定模式很可能是狗的图片，或者一种语言的句子特征匹配另一种语言的句子特征。解决复杂的方程式还需要具有处理符号数据的能力，例如方程b-4ac = 7中的字母。此类变量不能直接相加、相乘或相除，仅使用传统的模式匹配或统计分析，神经网络就仅限于极其简单的数学问题。

　　我们的解决方案是一种全新的方法，可将复杂的方程视为语言中的句子。这使得我们能够充分利用在神经机器翻译（NMT）被证明有效的技术，通过训练模型将问题从本质上转化为解决方案。要实现此方法，需要开发一种将现有数学表达式分解为类似语言语法的方法，并生成一个超过100M个配对方程和解的大规模训练数据集。

　　当出现数千个未知表达式时（这些方程并不是训练数据的一部分），我们的模型比传统基于代数的方程求解软件，例如Maple，Mathematica和Matlab，表现出更快的速度和更高的精度。这项工作不仅表明深度学习可以用于符号推理，而且还表明神经网络有潜力解决各种各样的任务，包括那些与模式识别不相关的任务。我们将分享我们的方法以及产生相似训练集方法的细节。

　　一种应用NMT的新方法

　　擅长符号数学的人经常依靠一种直觉。他们对给定问题的解决方案应该是什么有一种感觉，例如观察被积分函数中是否存在余弦，这意味着其积分可能存在正弦，然后进行必要的工作以证明这个直觉。这与代数所需的直接计算不同。通过训练模型来检测符号方程中的模式，我们相信神经网络可以将导致其解决方案的线索拼凑起来，大致类似于人类对复杂问题的基于直觉的方法。因此，我们开始探索将符号推理作为NMT问题，在该模型中，模型可以根据问题示例及其匹配的解决方案来预测可能的解决方案。

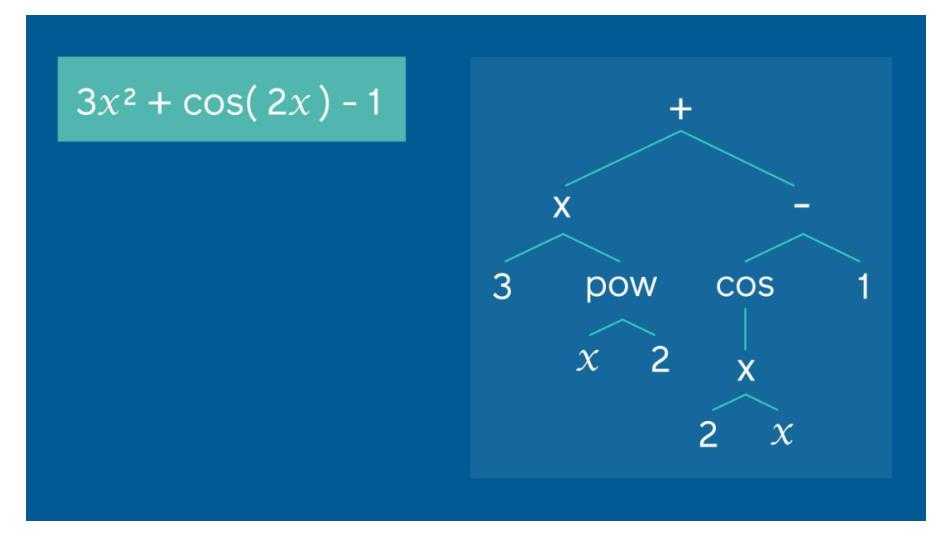
　　作为示例，我们的方法将展示如何把左侧的现有方程扩展为可以用作翻译模型输入的表达式树。对于该方程，输入到模型中的预序列为：（加，乘，3，乘方，x，2，减，余弦，乘，2，x，1）

　　为了使用神经网络实现此应用，我们需要一种新颖的方式来表示数学表达式。NMT系统通常是序列到序列（seq2seq）模型，使用单词序列作为输入，并输出新的序列，从而允许它们翻译完整的句子而不是单个单词。我们使用了两步方法将此方法应用于符号方程。首先，我们开发了一种有效地分解方程的过程，将被分解后的方程布置在树状结构的分支中，这个树状结构随后被扩展为与seq2seq模型兼容的序列。常量和变量充当叶子，而运算符（例如加号和减号）和函数是连接树的分支的内部节点。

　　尽管它看起来可能不像传统语言，但以这种方式组织表达式可为方程提供类似于语言的语法，数字和变量是名词，而运算符则充当动词。我们的方法使NMT模型可以学习将给定树状结构问题的模式与其匹配的方程的解（也表示为树）对齐，类似于将一种语言的句子与经过确认的翻译相匹配。这种方法使我们能够利用功能强大的现成的seq2seq NMT模型，将单词序列替换为符号序列。

　　建立新的训练数据集

　　尽管我们的表达式——树语法使NMT模型在理论上有可能有效地将复杂的数学问题转化为方程的解，但是训练这样的模型将需要大量示例。而且，因为在我们关注的两类问题（积分和微分方程）中，随机生成的问题并不总是具有解，所以我们不能简单地收集方程并将其输入系统。我们需要生成一个全新的训练集，其中包括重新构造为模型可读的表达式树的已解方程的示例。这产生了方程和解的二元组，类似于在各种语言之间翻译的句子语料库。我们的集合还必须比该领域以前的研究中使用的训练数据大得多，后者曾尝试对数千个示例进行系统训练。由于神经网络只有在拥有更多训练数据时才会表现得更好，因此我们创建了包含数百万个示例的集合。

　　建立此数据集需要我们整合一系列数据清洗和生成技术。例如，对于我们的符号积分方程，我们翻转了翻译方法：不是生成问题并找到其解决方案，而是生成解决方案并找到它们的问题（它们的导数），这是一件容易得多的任务。这种从解决方案中产生问题的方法（有时被工程师称为陷门问题）使创建数百万个积分示例变得可行。我们得出的以翻译为灵感的数据集包括大约1亿个配对示例，其中包含积分问题的子集以及一阶和二阶微分方程。

　　我们使用此数据集来训练具有8个attention head和6个层的seq2seq transformer模型。transformer通常用于翻译任务，而我们的网络旨在预测各种方程的解，例如确定给定函数的不定积分。为了评估模型的性能，我们向模型提供了5000种未知表达式，使系统识别出训练中未出现的方程模式。我们的模型在求解积分问题时显示出99.7％的准确度，对于一阶和二阶微分方程，它们的准确度分别为94％和81.2％。这些结果超出了我们测试的所有三个传统方程求解器的结果。Mathematica取得了次佳的结果，在相同的积分问题上准确度为84％，对于微分方程结果的准确度为77.2％和61.6％。我们的模型还可以在不到0.5秒的时间内返回大多数预测，而其他系统则需要几分钟来找到解决方案，有时甚至会完全超时。

　　我们的模型将左侧的方程式（Mathematica和Matlab都无法求解的方程式）作为输入，并且能够在不到一秒钟的时间内找到正确的解决方案（如上图所示）。

　　将生成的解决方案与参考解决方案进行比较，使我们能够轻松，准确地验证结果。但是我们的模型也为给定方程生成了多个解。这类似于机器翻译中发生的事情，在机器翻译中，有很多翻译输入句子的方法。

　　AI方程求解器的下一步是什么

　　目前，我们的模型适用于单变量问题，我们计划将其扩展为多变量方程。这种方法还可以应用于其他基于数学和逻辑的领域，例如物理领域，从而有可能开发出可帮助科学家进行广泛工作的软件。

　　但是我们的系统对于神经网络的研究和使用具有更广泛的意义。通过在以前认为不可行的地方发现一种使用深度学习的方法，这项工作表明其他任务可以从人工智能中受益。无论是通过将NLP技术进一步应用到传统上与语言没有关联的领域，还是通过在新的或看似无关的任务中对模式识别进行更开放的探索，神经网络的局限性可能来自想象力的局限，而不是技术。