汉诺塔问题详解

Posted 2020-11-10 awcxv

【问题背景】

A柱子上有a个从上到下半径依次递减的圆盘。
A是初始柱子 B是空柱子 C也是空柱子
你要求把A上的a个圆盘都放到C柱子上去
并且C柱子上最后的圆盘的次序也同初始的A柱子一样
在移动盘子的过程中,不能将大盘子放在小盘子上面
一次只能移动一个圆盘

【详解】

这个问题可以分为三个步骤:
1.将A柱子上上面的a-1个圆盘全都移动到B柱子上.
2.把A柱子上唯一的一个圆盘移动到C柱子上。
3.把B柱子上的a-1个圆盘全都移动到C柱子上。
需要注意的是,第1步和第3步实际上都是递归进行的。

我们先来看第1个步骤。
把A柱子上面的a-1个圆盘移动到B柱子上。
这个时候,我们会发现这是原问题的一个缩小版,都是3个柱子,只不过第一个柱子上你现在
只需要考虑最上面的a-1个圆盘了。然后条件还是一样,B,C柱子是空的,让你把这a-1个圆盘放到
[B]柱子上去(对!目标的柱子改了!)
但他本质上还是同一个问题,所以我们可以写出这么一个递归程序了
(a,b,c表示A,B,C柱子上每个柱子的圆盘个数)

void solve(char A,char B,char C,int a,int b,int c){
　　if (a==0){
　　　　说明没有任何圆盘要移动,直接return;
　　}
　　solve(A,C,B,a-1,c,b);//把A柱子上的a-1个盘子全都移动到B柱子上去,此时辅助的柱子是原来的C柱子了
　　//注意 函数的第三个参数总是圆盘的目标柱子,第二个参数总是辅助柱子
　　....
}

ok第一个步骤完成了。
(你们可能觉得 好像啥事情都没做啊)
但不要忘记了,我们这个solve(A,B,C,a,b,c)的任务就是把第一个参数代表的柱子上的盘子全都放到第三个参数所代表
的柱子上去,辅助柱子是第二个参数所代表的柱子。
(我之所以强调是第i个参数,是因为第一个参数并不总是代表A柱子.

所以我们应该信任sovle(A,C,B,a-1,c,b)这个递归过程,他确实帮我们完成了这件事的第一个步骤。
那么紧接着，第二个步骤

把A柱子上唯一的一个盘放到C柱子上去。
即

void solve(char A,char B,char C,int a,int b,int c){
　　if (a==0){
　　　　说明没有任何圆盘要移动,直接return;
　　}
　　solve(A,C,B,a-1,0,0);
　　cout<<A<<"柱子上最顶端的圆盘直接放到"<<C<<"柱子上";
　　...
}

接下来进行第三步，再递归地把第2根柱子上的a-1个盘子放到C柱子去.
这时你会发现,C柱子上那唯一的一个圆盘,实际上可以不用管它,因为他是最大的,所以谁放它上面都
无所谓,因此,我们可以就把它看成是空的柱子。
(而A柱子因为我们把它唯一的一个圆盘(在整个问题中可能这个柱子上不止有一个圆盘,但对于它这个
子问题来说,可以看成是已经空了的)放到C柱子上了,所以也是空的了)
所以问题变成把B柱子上的a-1个圆盘,经过辅助柱子A全都放到C柱子上。
因此我们可以调用递归
solve(B,A,C,a-1,0,0);
从而得到完整的程序:

void solve(char A,char B,char C,int a,int b,int c){
　　if (a==0){
　　　　说明没有任何圆盘要移动,直接return;
　　}
　　solve(A,C,B,a-1,0,0);
　　cout<<A<<"柱子上最顶端的圆盘直接放到"<<C<<"柱子上";
　　solve(B,A,C,a-1,0,0);
}

会发现其实b,c柱子对于我们来说总是空的,所以我们不必要记录他们的柱子的个数。
可以简化一下,只用n来记录A柱子上的圆盘的个数。

void solve(char A,char B,char C,int n){
　　if (n==0) return;
　　solve(A,C,B,n-1);
　　cout<<A<<"->"<<C<<endl;
　　solve(B,A,C,n-1);
}

主程序调用solve(‘A‘,‘B‘,‘C‘,n);

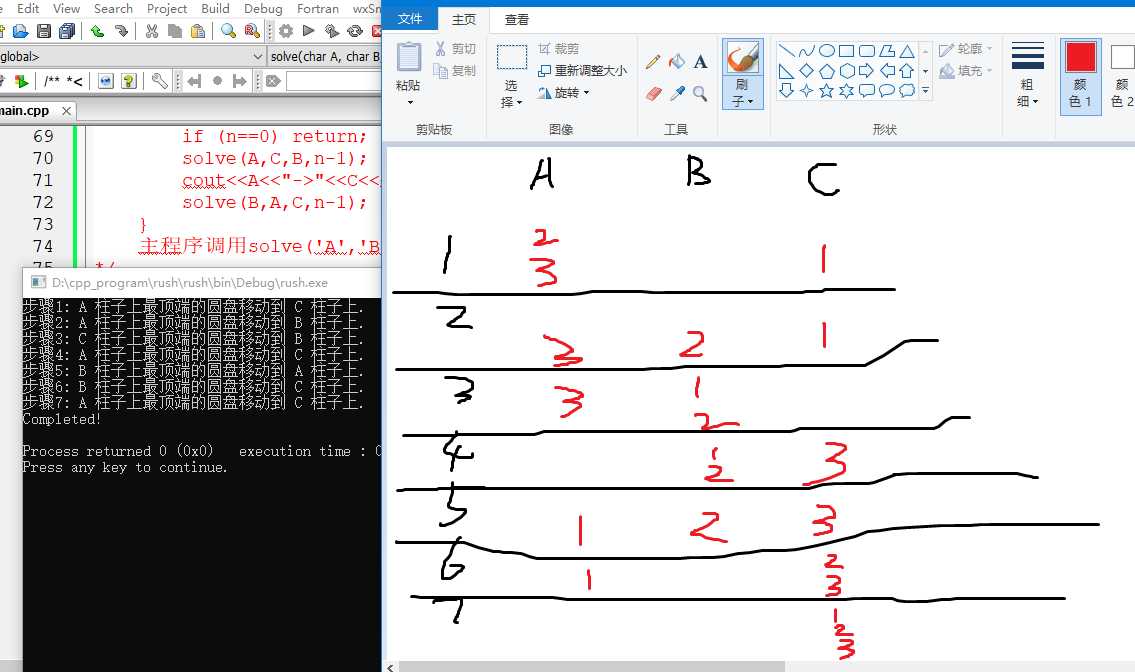
运行结果:(会发现操作步骤总是(2^n)-1哦