PTA 1007 Maximum Subsequence Sum

Posted 2021-02-20 shenc9ea

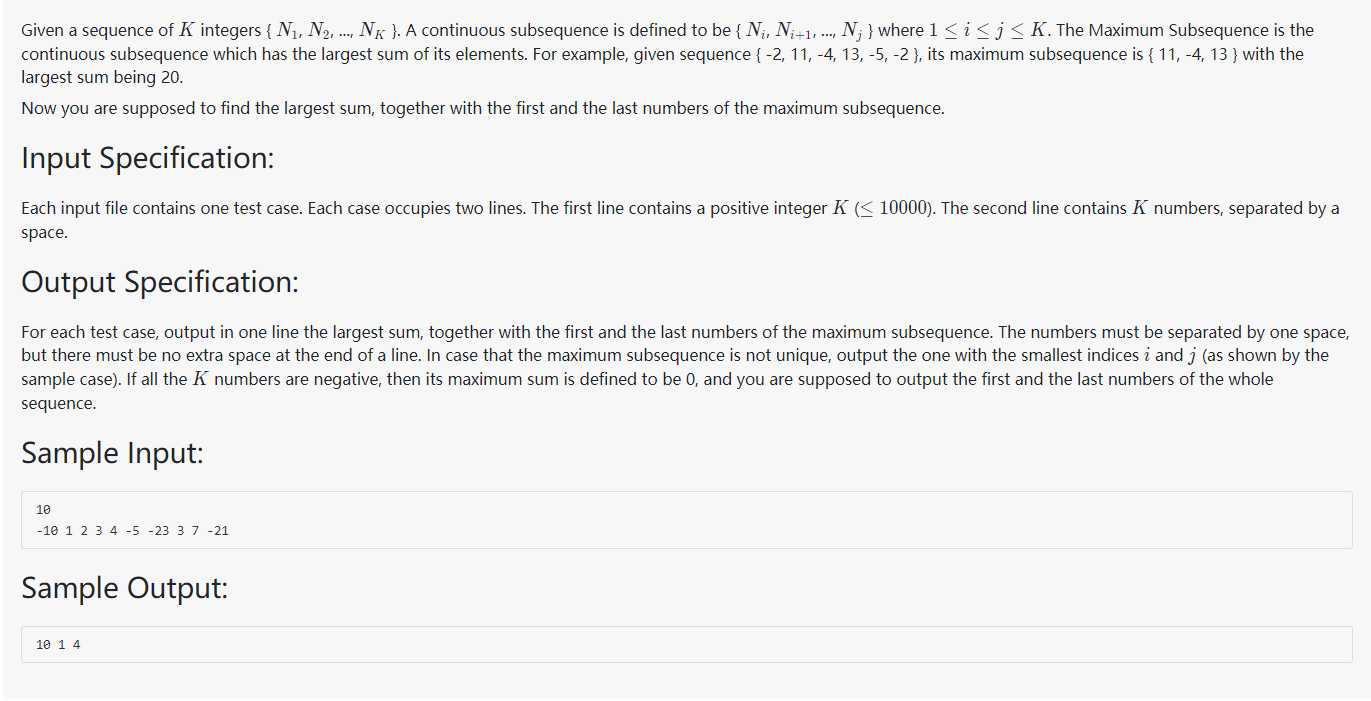
题目是浙大版数据结构视频里的原题，大意是说给出一个整数序列，让你求出和最大的连续子序列。最后输出子序列的和以及子序列的第一个数和最后一个数。如果给出的序列全是负数的话，就输出0以及整个序列的第一个数和最后一个数。

---

这道题大致有两种做法，一种是暴力枚举每一个子序列，当然毫无疑问会超时，还有一种是在线处理。我的在线处理做法是：

• 先定义一个last表示最大子序列的最后一个数，定义一个maxSum表示目前为止最大的子序列的和。定义一个sum用于表示当前子序列的和。

• 从第一个数开始处理。

  • 把当前的数加到sum上，如果加上之后sum小于0，说明无论之后的数是什么，加上当前这个序列之后都会比原来的小，那么我们果断把sum清零，重新开始累计。
  • 之后判断sum是否比maxSum大，如果大的话，我们更新last和maxSum。令last等于当前数的下标，maxSum等于sum。

• 继续往后处理，直到序列结束。

在上边那样处理完后，我们找出最大子序列和的问题是解决了。但还有一个问题，如果序列全是负数的话，sum会是0，last最后也会是0。如果序列中只有负数和0的话，最后的结果也会是sum和last都是0。这样就会导致两种情况无法区分。我的解决方法是最后从第1个数开始再找一遍，一旦找到0就可以判定是第二种情况，然后输出0 0 0，如果没有找到0，那就按第一种情况输出。

AC代码如下

#include <iostream>
#include <algorithm>
#include <stdio.h>
using namespace std;

int arr[10001];

int main()
{
    int k;
    cin >> k;

    for (int i = 0; i < k; i++)
        scanf("%d", arr + i);

    int sum = 0, maxSum = 0, last = 0, start = 0;

    for (int i = 0; i < k; i++)
    {
        sum += arr[i];
        if (sum < 0)
            sum = 0;
        else if (sum > maxSum)
        {
            maxSum = sum;
            last = i;
        }
    }
    int t = 0;
    start = last;
    while (start >= 0)
    {
        t += arr[start];
        if (t == maxSum)
            break;
        start--;
    }

    if (maxSum == 0)
    {
        bool flag = false;
        for (int i = 0; i < k; i++)
            if (arr[i] == 0)
            {
                printf("0 %d %d", arr[i], arr[i]);
                flag = true;
                break;
            }
        if (flag == false)
            printf("0 %d %d", arr[0], arr[k - 1]);
    }
    else
    {
        printf("%d %d %d", maxSum, arr[start], arr[last]);
    }

    return 0;
}