8.14动态规划例题：数字三角形

Posted 2021-02-20 z1110

/**
 * 数字三角形(POJ1163)<br>
 *
 * 在数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。<br>
 * 路径上的每一步都只能往左下或 右下走。只需要求出这个最大和即可，不必给出具体路径。<br>
 * 三角形的行数大于1小于等于100，数字为 0 - 99<br>
 * 输入格式：<br>
 * 5 //表示三角形的行数 接下来输入三角形<br>
 * 7<br>
 * 3 8<br>
 * 8 1 0<br>
 * 2 7 4 4<br>
 * 4 5 2 6 5<br>
 * 要求输出最大和<br>
 */

 

 

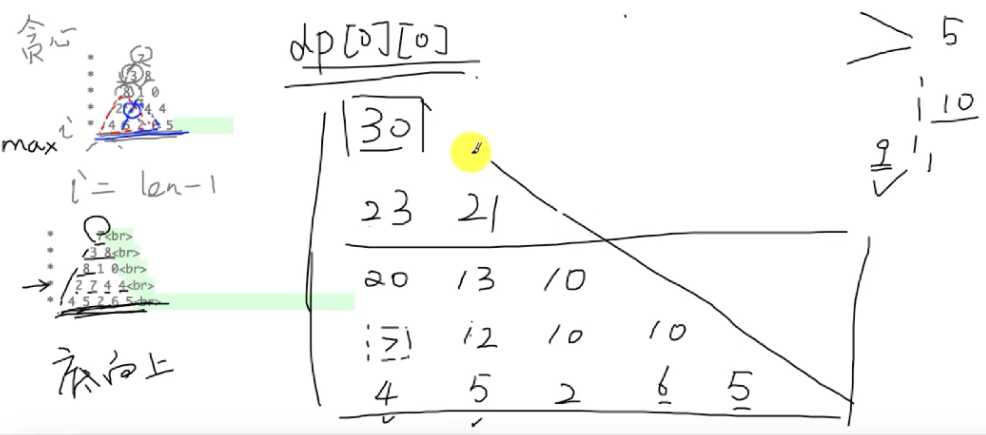
递归解法：每个顶点都有两个分支可以走。顶点的值 + max(左边支路的最大值,右边支路的最大值)。
记忆化递归解法：用两个变量记录 左边支路的最大值,右边支路的最大值，如果缓存没有值便递归。
dp解法：自底向上，先把最后一层放入新数组，然后从倒数第二层开始循环到顶层，dp[][]每层的每个顶点 + max(下一层左边的值，下一层右边的值)，直接返回dp[0][0]顶点的值。

 1 import java.util.Scanner;
 2 
 3 public class Eight_14动态规划例题_数字三角形 {
 4     //递归
 5     private static int maxSumUsingRecursive(int[][] triangle, int i, int j) {
 6         int rowIndex = triangle.length;
 7         if (i == rowIndex - 1) {
 8             return triangle[i][j];
 9         } else {
10             // 顶点的值+Max(左边支路的最大值,右边支路的最大值)
11             return triangle[i][j]
12                     + Math.max(maxSumUsingRecursive(triangle, i + 1, j),
13                             maxSumUsingRecursive(triangle, i + 1, j + 1));
14         }
15     }
16     //记忆型递归
17     private static int maxSumUsingMemory(int[][] triangle, int i, int j, int[][] map){
18         int rowIndex = triangle.length;
19         int value = triangle[i][j];
20         if(i == rowIndex - 1){
21             
22         }else{
23             //缓存有值，便不递归
24             int v1 = map[i+1][j];
25             if(v1 == 0){
26                 v1 = maxSumUsingMemory(triangle, i+1, j, map);
27             }
28             //缓存有值，便不递归
29             int v2 = map[i+1][j+1];
30             if(v2 == 0){
31                 v2 = maxSumUsingMemory(triangle, i+1, j+1, map);
32             }
33             value = value + Math.max(v1, v2);
34         }
35         map[i][j] = value;
36         return value;
37     }
38     //dp解法
39     private static int maxSumUsingDp(int[][] triangle, int i, int j){
40         int rowCount = triangle.length;
41         int columnCount = triangle[rowCount-1].length;
42         int[][] dp = new int[rowCount][columnCount];
43         //最后一行
44         for(int k = 0; k < columnCount; k++){
45             dp[rowCount-1][k] = triangle[rowCount-1][k];
46         }
47         //自低向上
48         for(int l = rowCount-2; l >= 0; l--){
49             for(int n = 0; n <= l; n++){
50                 dp[l][n] = triangle[l][n] + Math.max(dp[l+1][n], dp[l+1][n+1]);
51             }
52         }
53         return dp[0][0];
54     }
55     
56     public static void main(String[] args) {
57         Scanner in = new Scanner(System.in);
58         int n = in.nextInt();
59         int[][] triangle = new int[n][n];
60         for(int i = 0; i < n; i++){
61             for(int j = 0; j <= i; j++){ 
62                 triangle[i][j] = in.nextInt();
63             }
64         }
65 //        System.out.println(maxSumUsingRecursive(triangle, 0, 0));
66 //        System.out.println(maxSumUsingMemory(triangle, 0, 0, new int[n][n]));
67         System.out.println(maxSumUsingDp(triangle, 0, 0));
68     }
69 }