机器学习模型之感知机
Posted stephen-goodboy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习模型之感知机相关的知识,希望对你有一定的参考价值。
1、感知机模型
感知机是一个线性分类器,感知机的公式是
其中
感知机说得是我们有一系列的点x = (x1,x2,x3...xn)和相应的参数w = (w1,w2,w3....wn),我们将x和w向量进行乘积操作,最终会得到一个数字,如果这个数字大于等于0,那么我们将其归为+1类别,否则,归为-1类别。
关于(wx+b)可以理解为一个超平面,展开就是(w_{1} x_{1} + w_{2}x_{2} +w_{3}x_{3} + ...... +b),当(wx+b = 0)时,其表示的就是一个超平面,在二维空间如下图所示
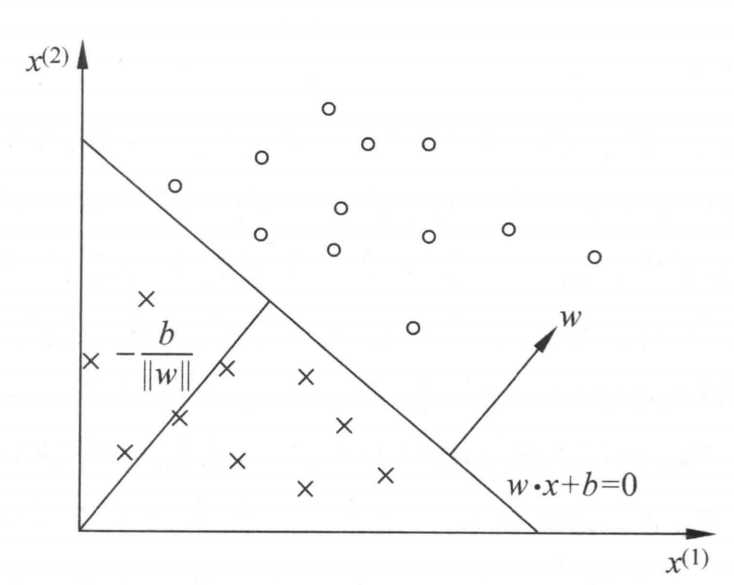
2、感知机策略
那么我们如何学习感知机的参数w呢?我们的策略就是构建损失函数,那么如何构建损失函数呢?我们想到的一种方法是误分类点的个数作为损失函数,但是这种方法的结果对w和b不可导,那么,我们就想出了另外一种策略,对于误分类的数据,其有一个性质
当(y_{i} = +1,wx_{i} + b = -1)时,(-y_{i} (wx_{i} + b) > 0),当(y_{i} = -1,wx_{i} + b = +1)时,(-y_{i} (wx_{i} + b) > 0),那对于分类正确的点怎么办呢?很简单,我们就不管他就行,或者他们的损失就是0,我们加上0就可以了。所以我们的损失函数就是所有误分类点的集合,如下面公式所示
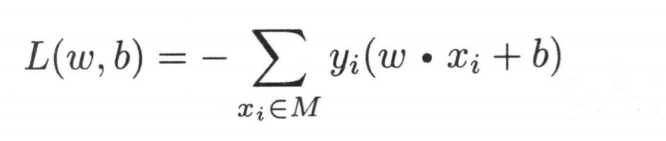
3、感知机算法
那我们如何来求解w和b呢,常用的策略就是对相应的参数进行求导,利用梯度下降法更新参数,求导结果为
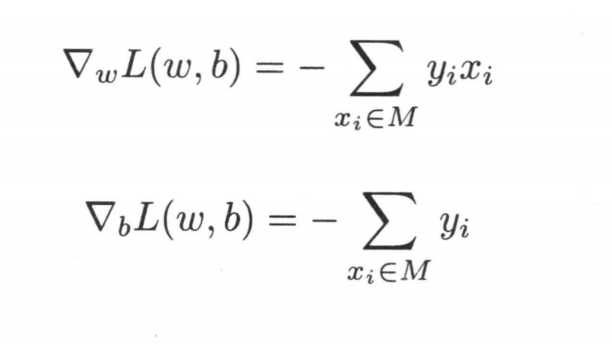
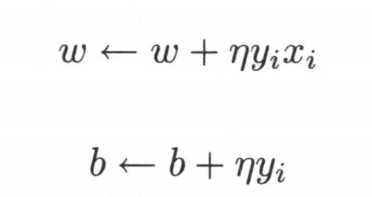
以上是关于机器学习模型之感知机的主要内容,如果未能解决你的问题,请参考以下文章