1353E K-periodic Garland

Posted 2021-02-19 starroadtang

题面

 

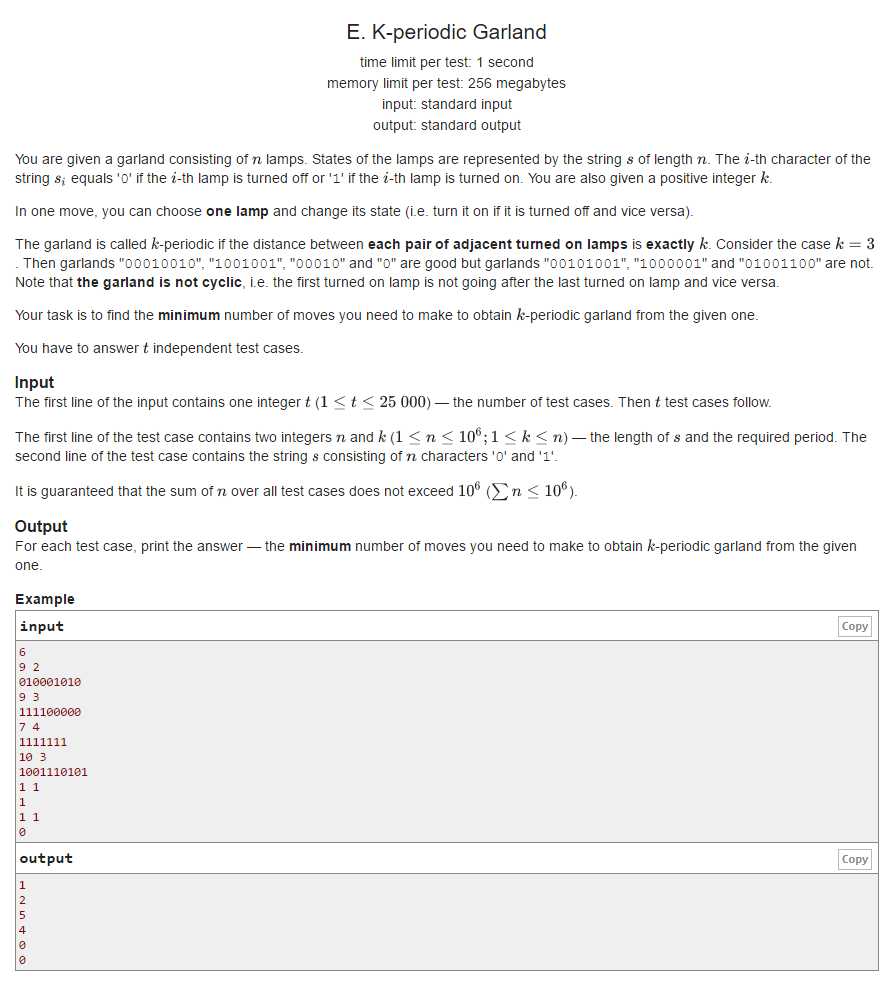
题目链接

 

https://codeforces.com/contest/1353/problem/E

 

题目大意

 

给你一个长度为 N 的 01 字符串和一个整数 K

每次操作你可以选择一个字符并改变其状态

现要使字符串中相邻 1 的距离为 K ，问最少需要操作几次

 

解题思路

 

因为每个相邻 1 的距离要求为 K

所以对于每个长度为 K 的区间最多只能有一个 1

提供两种做法

① dp

我们定义 pre[i] 为前 i 项 1 的个数

定义 dp[i][0] 为前 i 项都合法 , 第 i 位为 0 的最小操作次数

定义 dp[i][1] 为前 i 项都合法 , 第 i 位为 1 的最小操作次数

那么可得转移方程

dp[i][0] = min(dp[i - 1][0] , dp[i - 1][1] + s[i] == ‘1‘

dp[i][1] = min(dp[i - k][1] + pre[i - 1] - pre[i - k] , pre[i]) + s[i] == ‘0‘

当前 i - 1 项合法时，第 i 项为 0 ，那么前 i 项必定合法

当前 i - k 项合法时，第 i 项为 1 ，那么仅当第 i - k 为 1，且 i - k + 1 ~ i - 1项为 0 时，前 i 项合法

最后 ans = min( dp[n][0] , dp[n][1] ) 

②贪心

定义 sum 为起初字符串中 1 的总个数

我们可以先将整个字符串都变为 0，那么此时的代价为 sum

由于相邻的 1 的距离为 K，所以具有周期性质，且每个周期内 1 的个数只有一个

所以我们可以枚举每个周期的对应位置并将其改变为 1

每次枚举我们定义一个 cnt = 0 ，其意义为可以减少的代价

当 s[i] == ‘1‘ 时，cnt -- , 即减去起初把 s[i] 变为 0 的代价，当 s[i] == ‘0‘ 时，cnt ++ , 即把 s[i] 变为 1 的代价

每操作完一个周期区间，我们更新一次 cnt 和 ans，cnt = min(cnt , 0) , ans = min(ans , sum + cnt)

cnt = 0 即表示前面的周期区间对应位置的值保持为 0

 

AC_Code ①

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int pre[N] , dp[N][2];
char s[N];
signed main()
{
    ios::sync_with_stdio(false);
    int t; 
    cin >> t;
    while(t --)
    {
        int n , k;
        cin >> n >> k >> s + 1;
        for(int i = 1 ; i <= n ; i ++) pre[i] = pre[i - 1] + s[i] - ‘0‘;
        for(int i = 1 ; i <= n ; i ++)
        {
            int p = max(0 , i - k);
            dp[i][0] = min(dp[i - 1][0] , dp[i - 1][1]) + (s[i] == ‘1‘); 
            dp[i][1] = min(pre[i - 1] , dp[p][1] + pre[i - 1] - pre[p]) + (s[i] == ‘0‘);    
        }
        cout << min(dp[n][0] , dp[n][1]) << ‘
‘ ;
        for(int i = 0 ; i <= n ; i ++) dp[i][0] = dp[i][1] = pre[i] = 0;
    }
    return 0;
}

 

AC_Code ②

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
char s[N];
signed main()
{
    ios::sync_with_stdio(false);
    int t;
    cin >> t;
    while(t --)
    {
        int n , k , sum = 0 , ans = 0x3f3f3f3f;
        cin >> n >> k >> s + 1;
        for(int i = 1 ; i <= n ; i ++) sum += s[i] - ‘0‘;
        for(int i = 1 ; i <= k ; i ++)
        {
            int cnt = 0;
            for(int j = i ; j <= n ; j +=k)
            {
                if(s[j] == ‘1‘) cnt -- ;
                else cnt ++ ;
                cnt = min(cnt , 0);
                ans = min(ans , sum + cnt);
            }
        }
        cout << ans << ‘
‘  ;
    }
    return 0;
}