计算方法四参数正弦函数高斯牛顿法拟合

Posted 2021-02-19 ctpoqaq

四参数正弦函数高斯牛顿法拟合

---

 先给出几个主要的参考资料：

这个过程比较详细，我主要参考的是这个：https://wenku.baidu.com/view/70d5d05f312b3169a451a401.html

这个对概念介绍的比较清楚：https://wenku.baidu.com/view/5f5270bb5ff7ba0d4a7302768e9951e79a896944.html?fr=search

其他参考：

https://wenku.baidu.com/view/a6ac0bef19e8b8f67c1cb92a.html

知网论文：四参数正弦曲线拟合的一种收敛算法_梁志国

百度百科：https://baike.baidu.com/item/%E9%AB%98%E6%96%AF%E2%80%94%E7%89%9B%E9%A1%BF%E8%BF%AD%E4%BB%A3%E6%B3%95/15667583?fromtitle=%E9%AB%98%E6%96%AF%E7%89%9B%E9%A1%BF%E6%B3%95&fromid=9868498&fr=aladdin

---

 前言：

　　前些天写了计算方法与实现的论文，为了完成论文中模型的搭建，特意去学习了正弦函数的参数拟合方法。在这里记录一下。

方法简介：

　　有待拟合正弦函数：

 

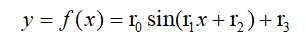
　　对于该函数f(x)，由于其四个未知参数分布复杂，是一个求非线性方程组解的最小平方和的问题，因此它难以直接使用最小二乘法来进行拟合。经典的高斯牛顿法拟合四参数正弦函数具体方法如下：

　　对于正弦函数记待估计系数向量为，则在此系数下， 记。

　　假设已知n个点 ，要使用以上点集拟合函数 f(x)，则需使得残差平方和最小。

　　也就是使

　　

　　设，对上述偏微分方程进行求导化简，易得以下非线性方程组

   

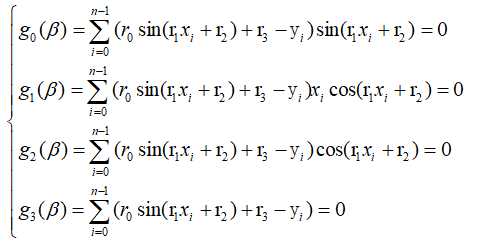
　　此时需要采用高斯牛顿法解此四元非线性方程组。

　　记向量函数：

　

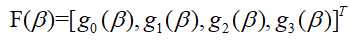
　　以及雅可比矩阵

 　

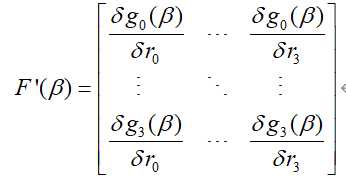
　　对于某个系数向量近似解，对向量函数做一阶Taylor展开，得：

　　 

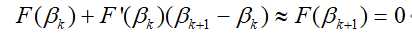
　　至此，我们实际上得到了一个Newton迭代公式，即：

　　

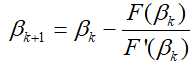
　　只需要设置初值，并代入迭代式进行一定次数的迭代，就能求出指定收敛精度下的近似解，使得残差平方和逼近最小。

---

 

　　在计算时，可记，将牛顿迭代式转变成：

　　

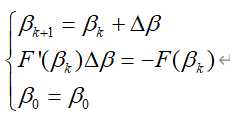
　　该式第二行为线性方程组：

　　 

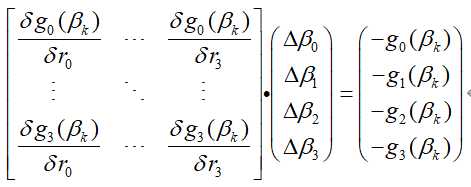
　　此线性方程组可使用高斯消元法或雅可比迭代法求解。

　　，为指定精度，当时即可停止迭代。

　　在使用高斯牛顿法解正弦函数拟合问题时，需格外注意初值，初值选取不当可能会导致迭代发散或者收敛到局部最优值上。