数据结构学习-第三次总结

Posted 2021-02-19 mikehro

图总结

1.思维导图

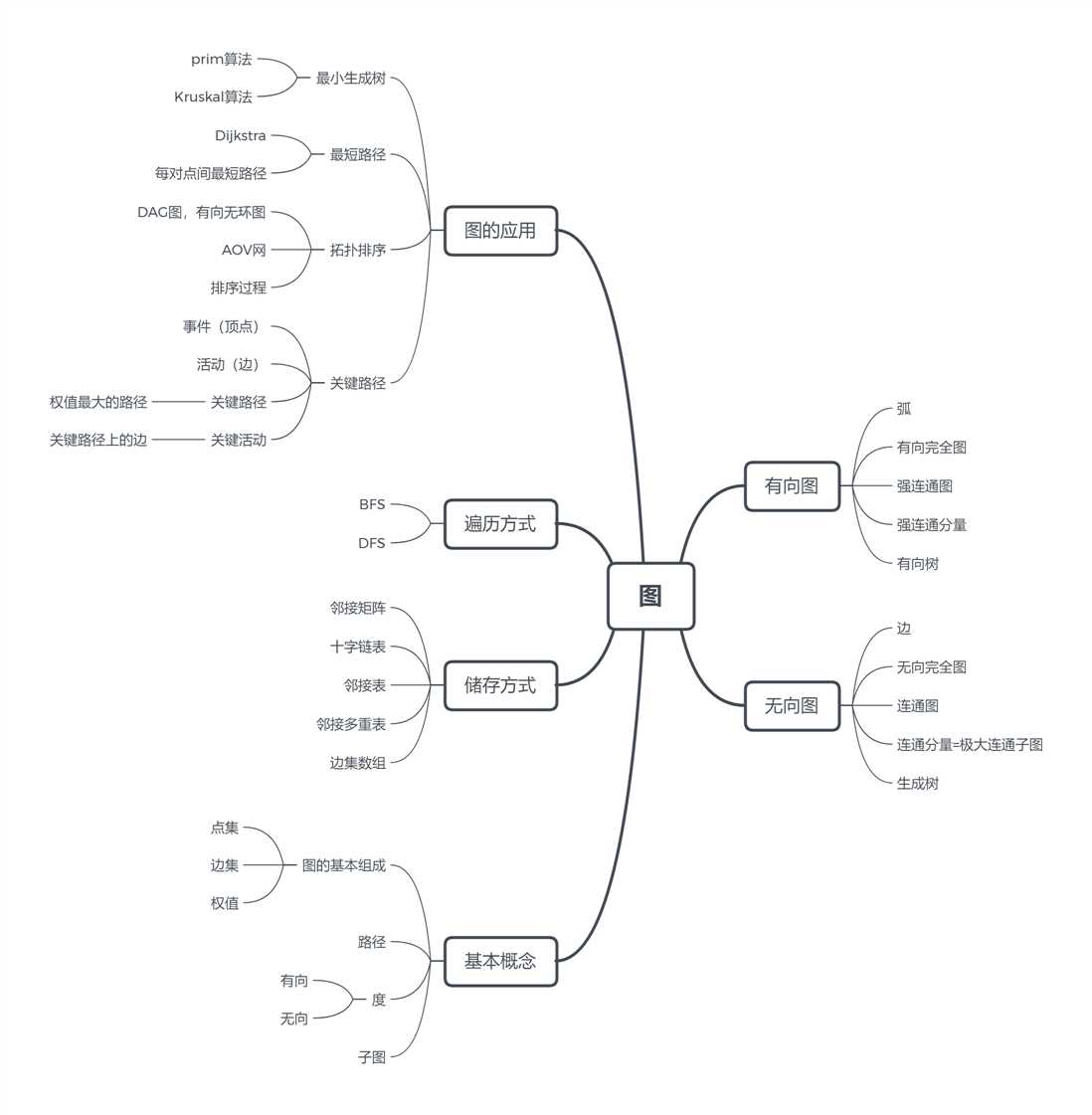
2.要点总结

1.定义

G=(V,E)

顶点偶对：（通常不考虑自环，即认为vi, vj不同）

(vi, vj)，无向边、无向图，vi, vj 互为邻接点

<vi, vj>，有向边、有向图，vi 为 vj 的邻接点，vi为弧尾、vj为弧头

带权的图称为网络。

2.基本术语

1、度（TD）、入度（ID）、出度（OD）：各节点度的和等于边数的2倍：2e=(i=1~n)Σ TD(vi)，有向图、无向图均如此。有向图入度和、出度和、边数 三者相等。

=> 无向图度和最大为n(n-1)，故边数最多n(n-1)/2，此时为完全图。

有向图度和最大为2n(n-1)，故边数最多n(n-1)，此时为有向完全图。

=> 稠密图、稀疏图（边或弧的数目是否接近完全图）

2、路径：若顶点序列v1v2...vm有(vi,vi+1)∈E(i=1,2,...m-1)，则为v1到vm的一条路径，有向图类似。

回路或环：起点、终点重合的路径。判断是否有回路可用下面介绍的深度优先遍历或拓扑排序。

简单路径：序列中顶点不重复的路径

简单回路或简单环：除首末顶点外其他顶点均不重复的回路

有根图：有向图若存在一个顶点有到其他所有顶点的路径，则为有根图，此顶点为根

3、子图：G,=(V,, E,)，其中 G, ? G、V, ? V, E, ? E

4、连通：

顶点连通：无向图顶点vi到vj（i≠j）有路径，则vi vj连通；有向图则要求vi到vj及vj到vi（i≠j）都有路径才是连通

连通图：无向图任意两个顶点间都是连通的则是连通图。对于一有n个顶点的无向图：若是连通图则边数：[n-1, n(n-1)/2]；若要保证是连通图则边至少需是 ：(n-1)(n-2)/2+1，即此时n-1个顶点构成完全图然后再加一条边。

强连通图：有向图任意两顶点间都是连通的则是强连通图。对于一有n个顶点的有向图，若是强连通图则边数：[n, n(n-1)]；若要保证是连通图则边至少需是：(n-1)(n-2)+2。

连通分量：无向图的极大连通子图。

强连通分量：有向图的极大连通子图。

连通图的连通分量只有一个即为本身，而非连通图的连通分量有多个；强连通图亦然。

5、生成树：连通图包含n个顶点的极小连通子图为其生成树。

连通图才有生成树，其包含n个顶点、n-1条边；生成树可能不唯一，且不一定是最小生成树。

3.图的存储

无向图：邻接矩阵、邻接表、多重邻接表法

有向图：邻接矩阵、邻接表、十字链表法

1、邻接矩阵存储（存所有边，若不带权则不存在的边包括自己到自己表示为0、若带权则表示为∞）

无向图的邻接矩阵是个对称阵，可以用矩阵的压缩存储。

2、邻接表存储（存顶点和邻接的边）：顺序存储与链式存储相结合。（顶点节点、边节点）

无向图邻接表中顶点节点、边节点数分别为n、2e，有向图的则分别为n、e。故无向图邻接表边节点数为偶数，若边节点数为奇数则为有向图。

有向图 第i行非0元素的个数（邻接矩阵存储）或第i个链表边节点的个数（邻接表存储） 等于该节点的出度OD，所有行非0元素个数和或所有链表边节点个数和等于边数e。

无向图 第i行非0元素的个数（邻接矩阵存储）或第i个链表边节点的个数（邻接表存储） 等于该节点的度TD，所有行非0元素个数和或所有链表边节点个数和等于两倍边数2e。

4.图的遍历

指访问每个顶点一次且仅一次。

遍历的过程实质上是通过边或弧寻找邻接点的过程，而采用不同遍历方法时总边节点数是不变的，所以深度优先、广度优先的时间复杂度一样。针对不同存储方法（邻接矩阵、邻接表）的遍历算法类似。

深度优先遍历（DFS）
广度优先遍历（BFS）

5.AOV、AOE网络

AOV、AOE网络都是有向图。

1、AOV网络用节点表示活动，一些活动间有先后关系，所以组成了有向图。

判断活动能否顺利开展（即图是否有环）：拓扑排序、深度优先遍历，时间复杂度均为O(n+e)

2、AOE网络：顶点表示事件、边表示活动。某顶点表示的事件发生后从该顶点出发的各有向边表示的活动才能发生；进入某顶点的各有向边表示的活动发生后该顶点表示的事件才能发生。

事件最早发生时间：从前往后，多入取大者（因为不能早于入活动的结束时间）

事件最晚发生时间：从后往前，多出取小者（因为不能晚于出活动的开始时间）

活动最早发生时间：从前往后，前驱事件的最早发生时间

活动最晚发生时间：从后往前，后继事件的最晚发生时间减当前活动的时间

松弛时间：活动最早发生时间与最晚发生时间的差值

关键路径：松弛时间为0的活动构成的路径，其权值和为网络的最大路径长度（Dijkstra等则可以求最短路径，注意区别），亦为工程的最短完成时间。路径可能不唯一，但权值和一样。

3.疑难问题及解决方案

广度优先遍历的算法问题（非递归）

广度优先遍历中，访问的邻接点如何判断是否已经访问，改用什么样的方式进行储存？

解决办法

使用回溯算法，采取一种分层的顺序搜素过程（无需判断是否已经访问），而不是递归。

从图中某顶点v出发：

访问顶点v
访问顶点v所有未被访问的邻接点、a1、a2…an，并用栈或队列存储
依次取出邻接点进行广度优先遍历

代码展示

void BFSTraverse(Graph G, void(*visit)(VertexType))
{
    for(v = 0; v < G.vexnum; v++)
        visited[v] = false;
    for(v = 0; v < G.vexnum; v++){
        if(!visited[v])
            BFS(G, v, Visit);
    }
}
void BFS(Graph G, int v, void(*Visit)(VertexType e))
{
    initqueue(Q);
    visited[v] = true;
    Visit(v);
    push(v);
    while(!empty(Q)){
        v = pop(Q);
        for(w = FirstAdjvex(G, v); w >= 0; w = NextAdjvex(G, v, w)){
            if(!visited[w]){
                visited[w] = true;
                Visit(w);
                push(w);
            }
        }
    }  
}