时间复杂度和空间复杂度计算方式

Posted 2021-02-18 mrlijavaengineer

一、时间复杂度

T(n)=O(f(n))。它表示随问题n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐进时间复杂度，简称为时间复杂度。

1、用常数1取代运行时间中的所有加法常数。

2、在修改后的运行次数函数中，只保留最高阶项。

3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

1.  int sum = 0, n = 100; /*执行一次*/
2.  sum = (1 + n) * n / 2; /*执行一次*/
3.  printf("%d",sum); /*执行一次*/

常数阶：单纯的分支结构(不包含在循环结构中)，其时间复杂度是0(1)。

1.  int i;
2.  for(i = 0; i < n; i++){
3.  /*时间复杂度为O(1)的程序步骤序列*/
4.  }

线性阶：循环体中的代码须要执行n次（循环体中是单纯的分支结构），其时间复杂度是O(n)。

1. int count = 1;
2.  while (count < n){
3.  count = count * 2;
4.    /*时间复杂度为O(1)的程序步骤序列*/
5.  }

对数阶：由2^x=n 得到x=logn。 所以这个循环的时间复杂度为O(logn)。

1.  int i, j;
2.  for(i = 0; i < n; i++){
3.  for(j = 0; j < n; j++){
4.  /*时间复杂度为O(1)的程序步骤序列*/
5.  } }

平方阶：时间复杂度为O(n)的语句，再循环n次。 所以这段代码的时间复杂度为O(n^2)。

1.  int i, j;
2.  for(i = 1; i < n; i++){
3.  for(j = 1; j < n; j++){
4.  for(j = 1; j < n; j++){
5.  /*时间复杂度为O(1)的程序步骤序列*/
6. }}}

立方阶：时间复杂度为O(n^3)。

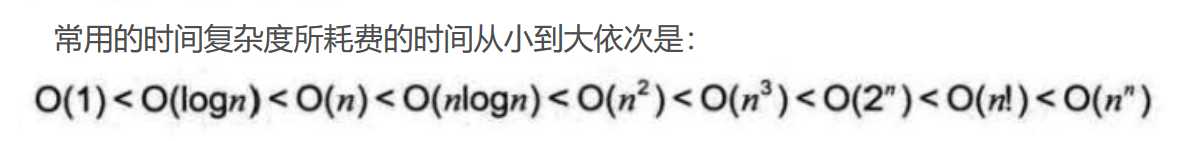
过大的n都会使得结果变得不现实。同样指数阶O(2^n)和阶乘阶O(n!)等除非是很小的n值，否则哪怕n 只是100，都是噩梦般的运行时间。

最坏情况运行时间是一种保证，那就是运行时间将不会再坏了。 在应用中，这是一种最重要的需求， 通常， 除非特别指定， 我们提到的运行时间都是最坏情况的运行时间。指最坏时间复杂度。

二、空间复杂度

算法的空间复杂度通过计算算法所需的存储空间实现，算法空间复杂度的计算公式记作:S(n)= O(f(n))，其中，n为问题的规模，f(n)为语句关于n所占存储空间的函数。

 

我们在写代码时，完全可以用空间来换取时间，比如说，要判断某某年是不是闰年，你可能会花一点心思写了一个算法，而且由于是一个算法，也就意味着，每次给一个年份，都是要通过计算得到是否是闰年的结果。 还有另一个办法就是，事先建立一个有2050个元素的数组(年数略比现实多一点)，然后把所有的年份按下标的数字对应，如果是闰年，此数组项的值就是1，如果不是值为0。这样，所谓的判断某一年是否是闰年，就变成了查找这个数组的某一项的值是多少的问题。此时，我们的运算是最小化了，但是硬盘上或者内存中需要存储这2050个0和1。这是通过一笔空间上的开销来换取计算时间的小技巧。

在做算法分析时，主要讨论的是时间复杂度。 从用户使用体验上看，更看重的程序执行的速度。一些缓存产品(redis, memcache)和算法(基数排序)本质就是用空间换时间。