PriorityQueue源码分析

Posted 2021-02-18 swifthao

顶部注释告诉我们的信息

• 一个无界的队列

• 基于优先级堆（Java中的PQ相当于最小堆）

• priority queue中的元素的顺序基于Comparable原始的顺序或者由构造时提供的Comparator提供

• priority queue中不能有null元素，有null元素还怎么比大小。当然也不允许插入一个不可比较(non-comparable)的对象(如果你插入一个non-comparable对象，则会抛出一个ClassCastException异常)

• priority queue是无界的，但是内部有capacity属性来管理用于存储数据的数组的大小（priority queue基于数组）

• iterator()不能保证按照指定顺序遍历pq中的元素，如果对遍历顺序有需求的话，使用Arrays.sort(pq.toArray())

• pq不是线程安全的，如果要使用线程安全的版本，使用java.util.concurrent.PriorityBlockingQueue

• 出队入队的时间复杂度：O(log(n))（因为要做上移和下移来保证顺序）

---

源码部分

一、定义

public class PriorityQueue<E> extends AbstractQueue<E>
    implements java.io.Serializable

二、属性

/**
     * Priority queue represented as a balanced binary heap: the two
     * children of queue[n] are queue[2*n+1] and queue[2*(n+1)].  The
     * priority queue is ordered by comparator, or by the elements‘
     * natural ordering, if comparator is null: For each node n in the
     * heap and each descendant d of n, n <= d.  The element with the
     * lowest value is in queue[0], assuming the queue is nonempty.
     */
    transient Object[] queue; 
    private int size = 0;
     /**
     * The comparator, or null if priority queue uses elements‘
     * natural ordering.
     */
    private final Comparator<? super E> comparator;
    transient int modCount = 0;

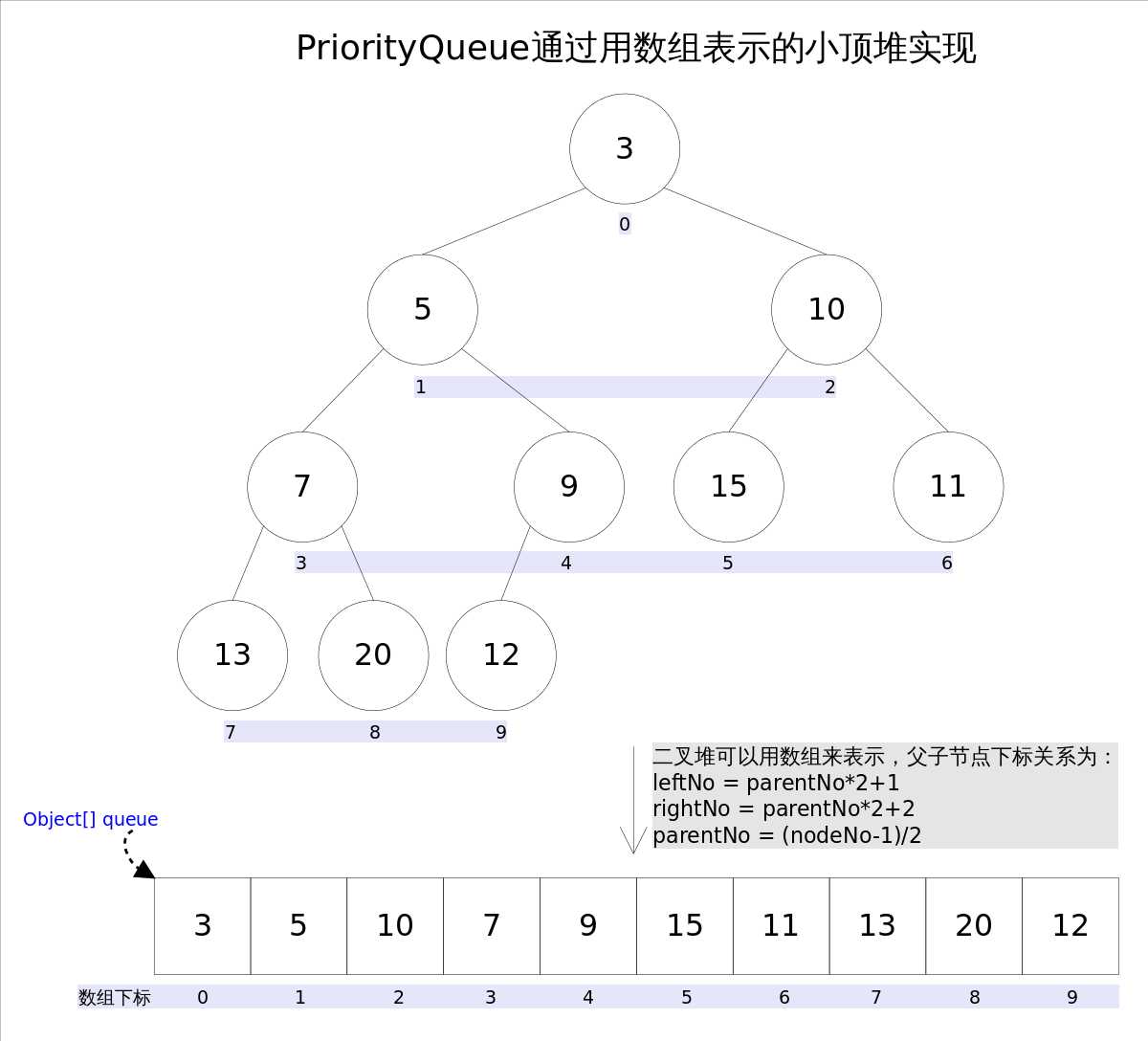
优先级队列表现为一个平衡二项堆(即，平衡二叉树)：queue[n]的两个儿子分别是queue[2n+1]和queue[2(n+1)]。优先级队列通过比较器(comparator)来排序，或者如果比较器为空则通过元素的自然顺序来排序：堆中每个节点n和n的每个后裔节点d，n <= d。假设队列是非空的，那么具有最低值的元素在queue[0]。

• leftNo = parentNo*2+1

• rightNo = parentNo*2+2

• parentNo = (nodeNo-1)/2

通过上述三个公式，可以轻易计算出某个节点的父节点以及子节点的下标。这也就是为什么可以直接用数组来存储堆

三、方法

1.grow方法

Double size if small; else grow by 50%

private void grow(int minCapacity) {
        int oldCapacity = queue.length;
        // Double size if small; else grow by 50%
        int newCapacity = oldCapacity + ((oldCapacity < 64) ?
                                         (oldCapacity + 2) :
                                         (oldCapacity >> 1));
        // overflow-conscious code
        if (newCapacity - MAX_ARRAY_SIZE > 0)
            newCapacity = hugeCapacity(minCapacity);
        queue = Arrays.copyOf(queue, newCapacity);
    }
private static int hugeCapacity(int minCapacity) {
        if (minCapacity < 0) // overflow
            throw new OutOfMemoryError();
        return (minCapacity > MAX_ARRAY_SIZE) ?
            Integer.MAX_VALUE :
            MAX_ARRAY_SIZE;
    }

2.offer(add方法是调用的offer方法）

public boolean offer(E e) {
        if (e == null)
            throw new NullPointerException();
        modCount++;
        int i = size;
        if (i >= queue.length)
            grow(i + 1);
        size = i + 1;
        if (i == 0)
            queue[0] = e;
        else
            siftUp(i, e);
        return true;
    }

插入操作会通过siftUp调整堆结构的，时间复杂度：O(log(n))

3.siftUp

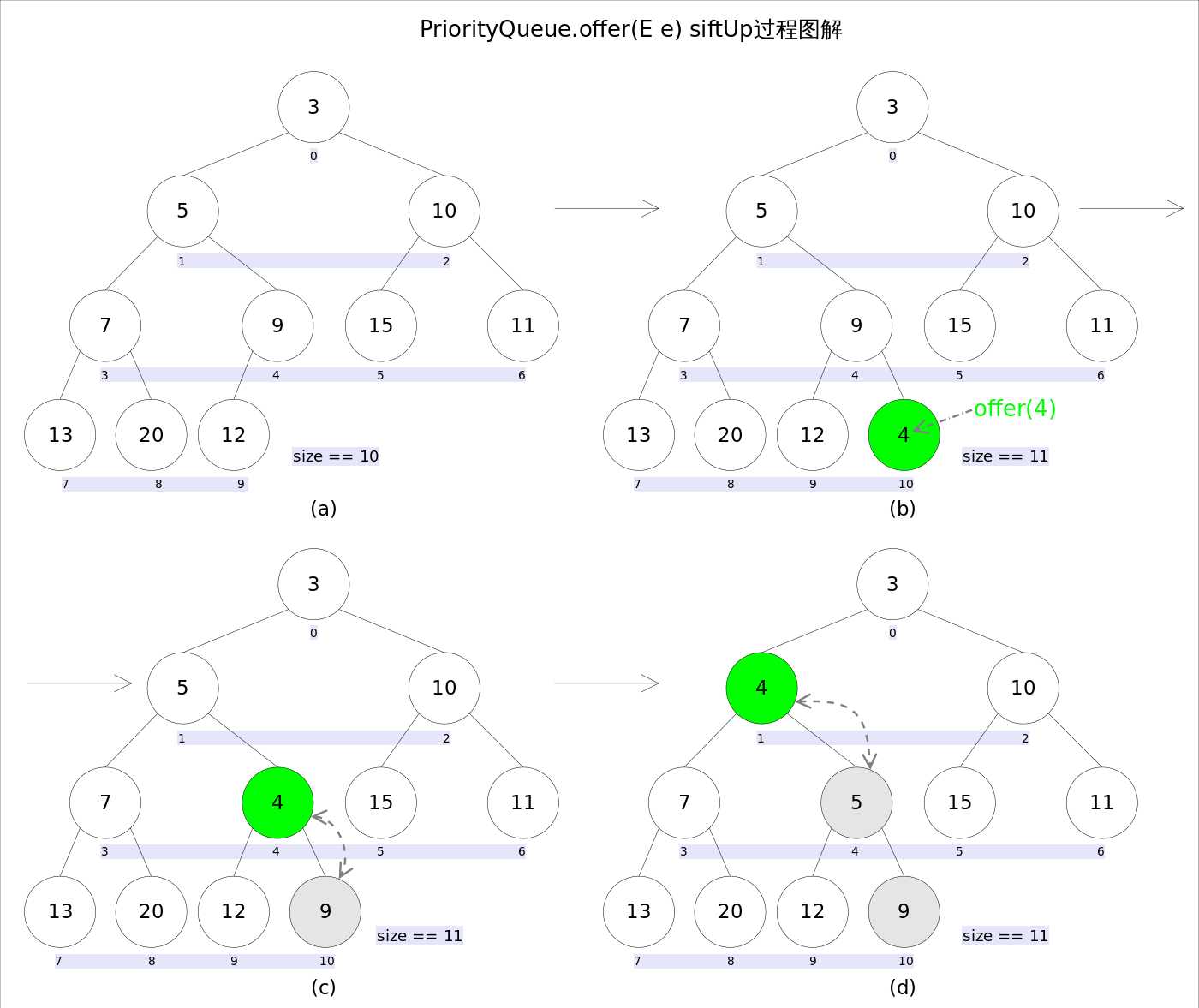
private void siftUp(int k, E x) {
        if (comparator != null)
            siftUpUsingComparator(k, x);
        else
            siftUpComparable(k, x);
    }

    @SuppressWarnings("unchecked")
    private void siftUpComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>) x;
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = queue[parent];
            if (key.compareTo((E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = key;
    }

    @SuppressWarnings("unchecked")
    private void siftUpUsingComparator(int k, E x) {
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = queue[parent];
            if (comparator.compare(x, (E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = x;
    }

补充：

• “>>>”代表无符号右移，不管要右移的数是正还是负，左边都填0

• “>>”代表有符号右移，右移正数左边补0，右移负数左边补1

4.element和peek

element()和peek()的语义完全相同，都是获取但不删除队首元素，也就是队列中权值最小的那个元素，二者唯一的区别是当方法失败时前者抛出异常，后者返回null。根据小顶堆的性质，堆顶那个元素就是全局最小的那个；由于堆用数组表示，根据下标关系，0下标处的那个元素既是堆顶元素。所以直接返回数组0下标处的那个元素即可。

public E peek() {
        return (size == 0) ? null : (E) queue[0];
    }

5.remove和poll

remove()和poll()方法的语义也完全相同，都是获取并删除队首元素，区别是当方法失败时前者抛出异常，后者返回null。由于删除操作会改变队列的结构，为维护小顶堆的性质，需要进行必要的调整。

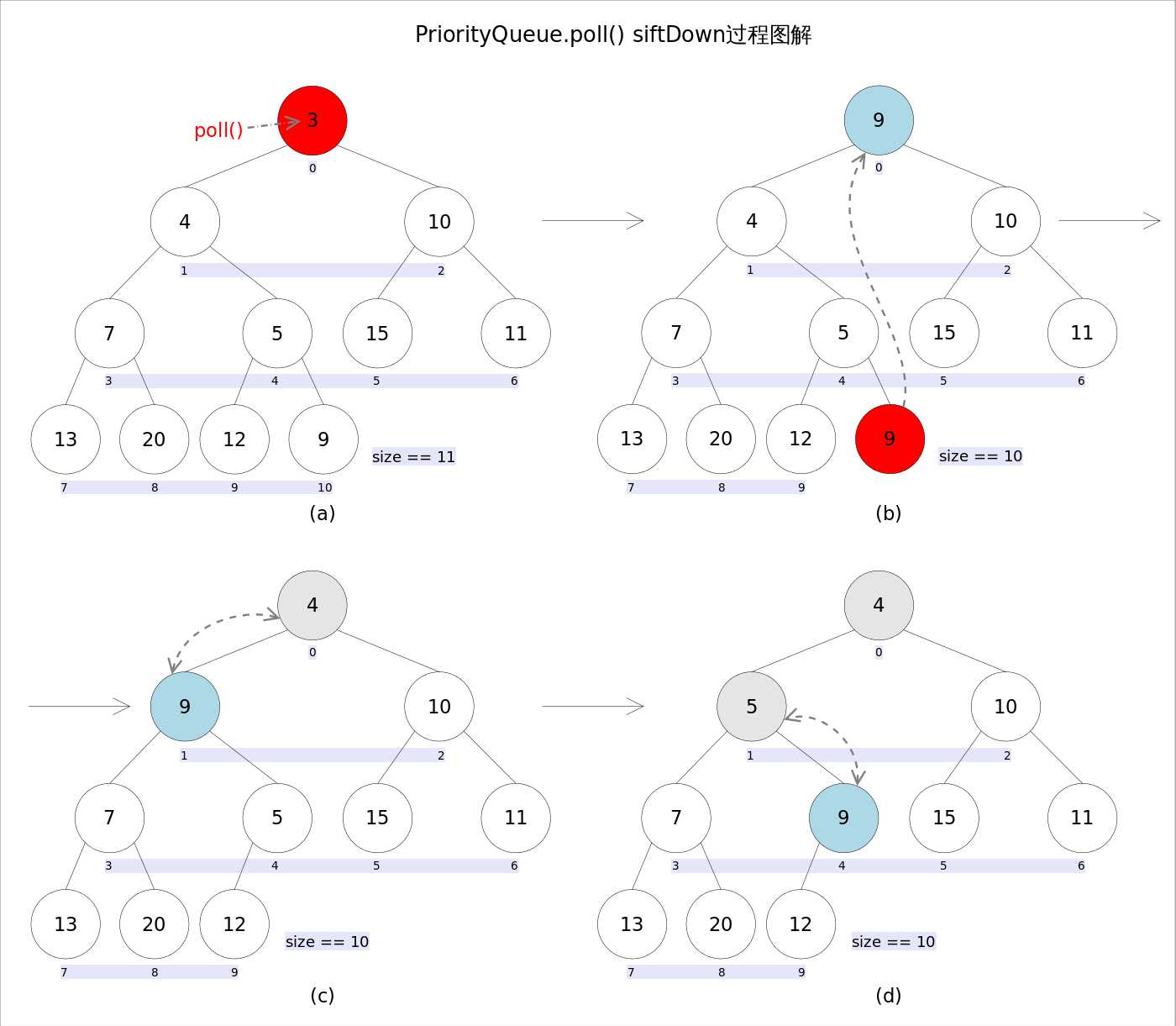
public E poll() {
        if (size == 0)
            return null;
        int s = --size;
        modCount++;
        E result = (E) queue[0];
        E x = (E) queue[s];
        queue[s] = null;
        if (s != 0)
            siftDown(0, x);
        return result;
    }

6.siftDown

private void siftDown(int k, E x) {
    int half = size >>> 1;
    while (k < half) {
        //首先找到左右孩子中较小的那个，记录到c里，并用child记录其下标
        int child = (k << 1) + 1;//leftNo = parentNo*2+1
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            comparator.compare((E) c, (E) queue[right]) > 0)
            c = queue[child = right];
        if (comparator.compare(x, (E) c) <= 0)
            break;
        queue[k] = c;//然后用c取代原来的值
        k = child;
    }
    queue[k] = x;
}

7.remove(Object o)

remove(Object o)方法用于删除队列中跟o相等的某一个元素（如果有多个相等，只删除一个），该方法不是Queue接口内的方法，而是Collection接口的方法。由于删除操作会改变队列结构，所以要进行调整；又由于删除元素的位置可能是任意的，所以调整过程比其它函数稍加繁琐。具体来说，remove(Object o)可以分为2种情况：1. 删除的是最后一个元素。直接删除即可，不需要调整。2. 删除的不是最后一个元素，从删除点开始以最后一个元素为参照调用一次siftDown()即可。此处不再赘述。

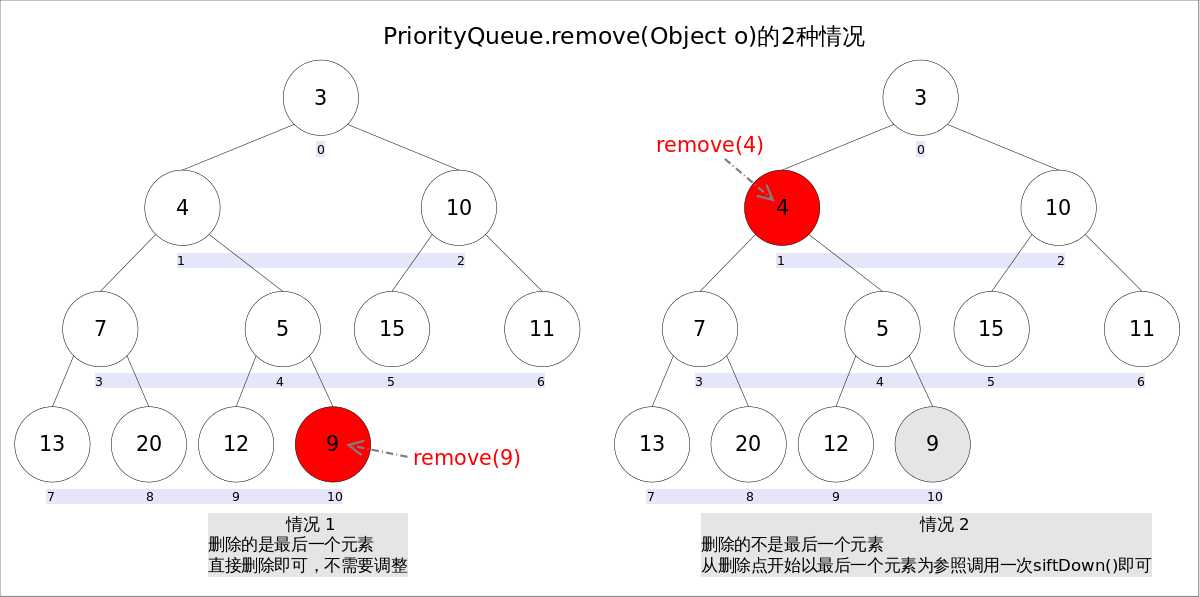
//remove(Object o)
public boolean remove(Object o) {
    //通过遍历数组的方式找到第一个满足o.equals(queue[i])元素的下标
    int i = indexOf(o);
    if (i == -1)
        return false;
    int s = --size;
    if (s == i) //情况1
        queue[i] = null;
    else {
        E moved = (E) queue[s];
        queue[s] = null;
        siftDown(i, moved);//情况2
        ......
    }
    return true;
}

---

参考链接

https://www.cnblogs.com/Elliott-Su-Faith-change-our-life/p/7472265.html