归并排序（递归非递归以及自然归并排序）算法总结

Posted 2020-11-09 gardener

注：本文所指归并排序指 二路归并排序。

归并排序是平均情况、最坏情况、最好情况时间复杂度都为O（Nlog2N）的稳定的排序算法。最近梳理了下归并排序的递归、非递归、以及自然归并排序算法。

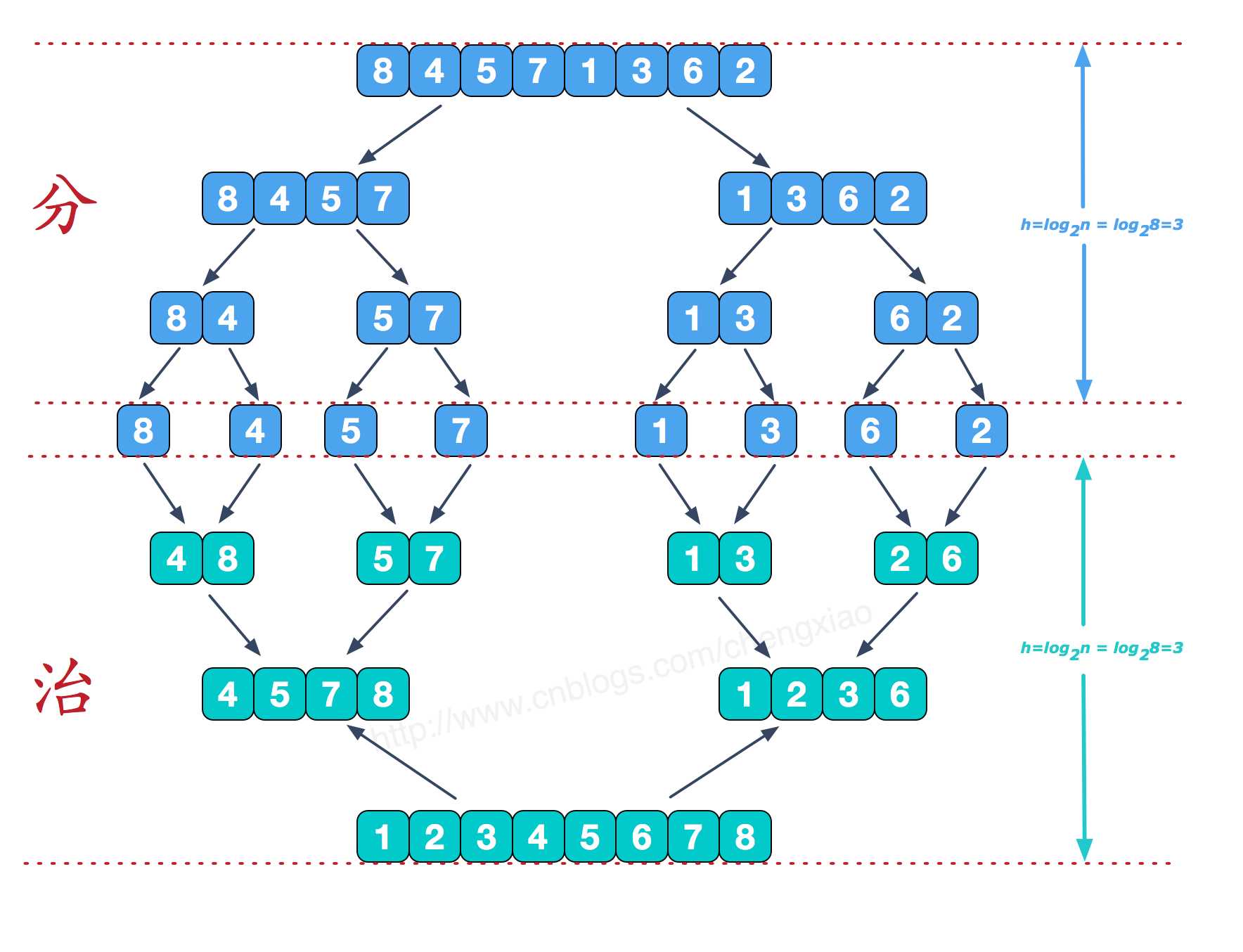
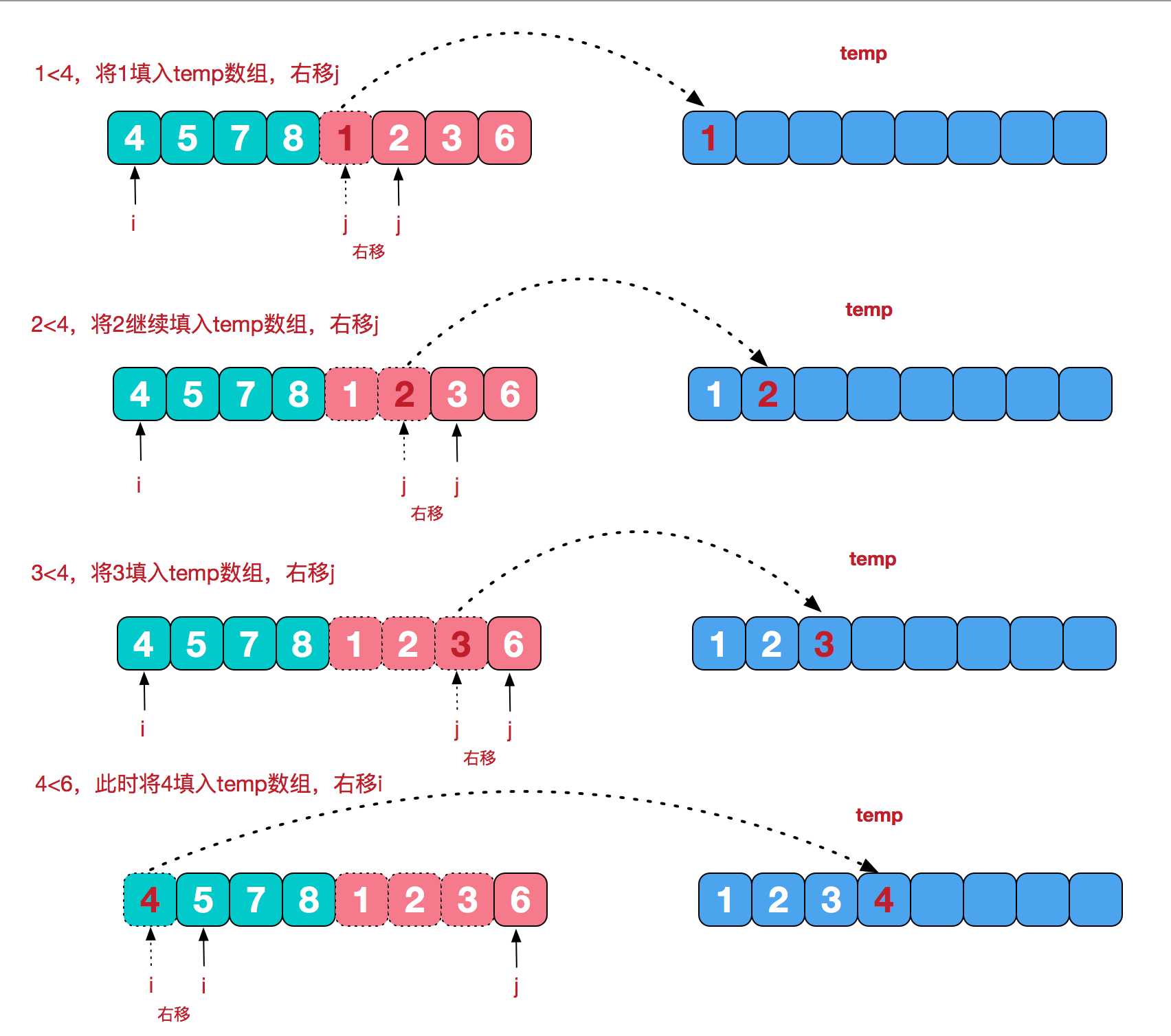
归并排序的基础：将两个有序数组合并为一个有序数组，需要O(n)的辅助空间。

图片来自：https://www.cnblogs.com/chengxiao/p/6194356.html

 

 

// array:待排序数组

//temparray: 临时数组

//startindex:起始下标

//middleindex: 中间值下标

//endindex:终止下标

void merge(int sourcearray[], int temparray[], int startindex, int middleindex, int endindex)
{
int left = startindex, index = startindex;
int right = middleindex + 1 ;
if (left >= right )
return;

//对两有序数组进行合并
while (left != middleindex + 1 && right != endindex + 1)
{
if (sourcearray[left ] <= sourcearray[right ])
{
temparray[index++] = sourcearray[left++];
}
else
{
temparray[index++] = sourcearray[right++];
}
}

//左边数组未合并完，直接合入
while (left!= middleindex+ 1)
{
temparray[index++] = sourcearray[left++];
}

//右边数组未合并完，直接合入
while (right != endindex + 1)
{
temparray[index++] = sourcearray[right++];
}

//将临时数组中排好序的数组赋值给排序数组

for (int i = 0; i < endindex+ 1; ++i)
{
sourcearray[i] = temparray[i];
}

}

 

 

归并排序递归算法：

void mergesort(int sourcearray[],int temparray[], int low ,int high)

{

if (low>=high)

return;

//一分为二

int middle = (low+high)/2;

//左半部分递归

mergesort(sourcearray, temparray, low,middle);

//右半部分递归

mergesort(sourcearray, temparray, middle+1,high);

//将左半部分和右半部分合并

merge(sourcearray,temparray,low,middle,high);

}

 

非递归归并排序算法：

非递归排序与递归排序相反，将一个元素与相邻元素构成有序数组，再与旁边数组构成有序数组，直至整个数组有序。

void merge_noncursive(int sourcearray[], int temparray[],int endindex)

{

   //步长，在i+step内数组有序，将sourcearray[i]...sourcearray[step-1]与sourcearray[i+step]...sourcearray[min(endindex,i+2*step-1)]两个有序数组合并起来。

    int step = 1;

    int index;

    while(step <= endindex)

     {  

　　　index = 0;

　　//将相邻数组合并

        while(index <= endindex - 2*step +1)

        {

   　　merge(sourcearray,temparray,index,index+step -1,index+2*step -1);

           index += 2*step;

        }

        //合并有序的左半部分以及不及一个步长的右半部分

 　　if (index + step <= endindex)

         {

　　　　merge(sourcearray,temparray,index,index+step-1,endindex);

         }

       step *= 2;

     }

}

 

 

自然归并排序：

既然归并排序是将多个有序的数组合并成一个数组，除了完全逆序的数组，总有一部分数组是有序的，我们可以获取有序数组的标记，从而将多个有序数组合并成一个有序数组。

//这个是理解自然归并排序的关键

int getindex(int array[], int flag[],int index)

{

   int next = 0;

　//最开始为下标0

   flag[next] = 0;

   next++;

  for(int i = 0;i<index;i++)

   {

    //找到数组元素不是有序的地方

    if (array[i] > array[i+1])

     {

　　flag[next++] = i;

　 }

  }    

       //最后一位为最大下标

　　flag[next] = index;

     return next;

}

void merge_naturally(int sourcearray[],int temparray[],int index)

{

　　int * flag = new int[index];

       int num = getindex(sourcearray,flag,index);

     //大于等于2说明除了0与index外有其他数，数组不完全有序

       while(num >= 2)

      {       

　　　　//对相邻有序数组进行合并

              for(int i = 0; i<=num;i+=2)

　　　　{

               merge(sourcearray,temparray,flag[i],flag[i+1],flag[i+2]);

             }

　　　//继续获取无序的序号

          num = getindex(sourcearray,flag,index);

      }

}