大话数据结构 树1

Posted 2021-02-17 expedition

树的定义

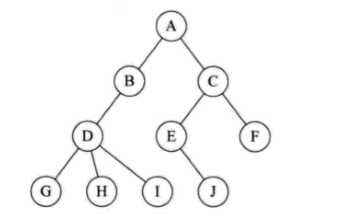
下图，子树T1,子树T2就是跟结点A的子树：

 

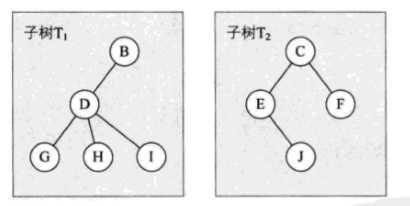
强调：

• n>0时 ，根结点唯一
• m>0时，子树的个数没有限制，但一定互不相交

 

结点分类

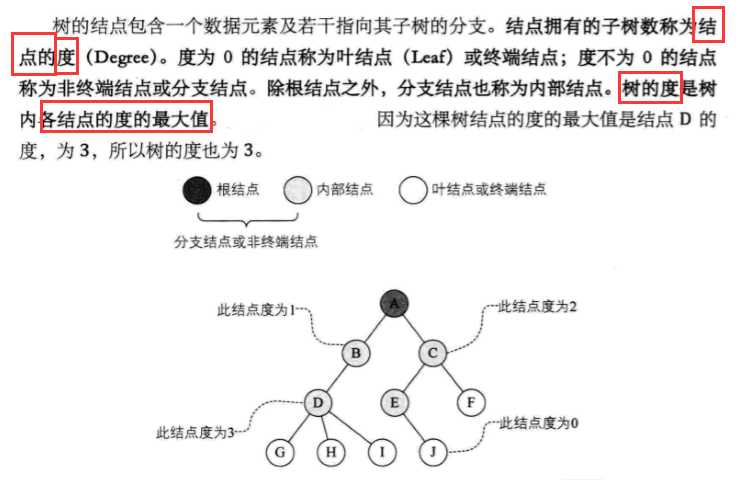
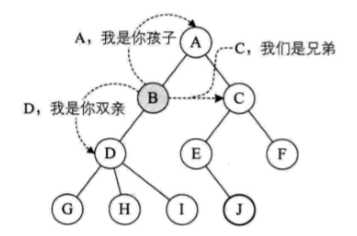
结点间的关系

结点的子树的根称为该结点的孩子

该结点称为孩子的双亲

同一个双亲的孩子之间互称兄弟

结点的祖先是从根到该结点所经分支上的所有结点

所以对于H来说，D、B、A都是 它的祖先

以某结点为根的子树中的任一结点都称为该结点的子孙

 树的其他概念

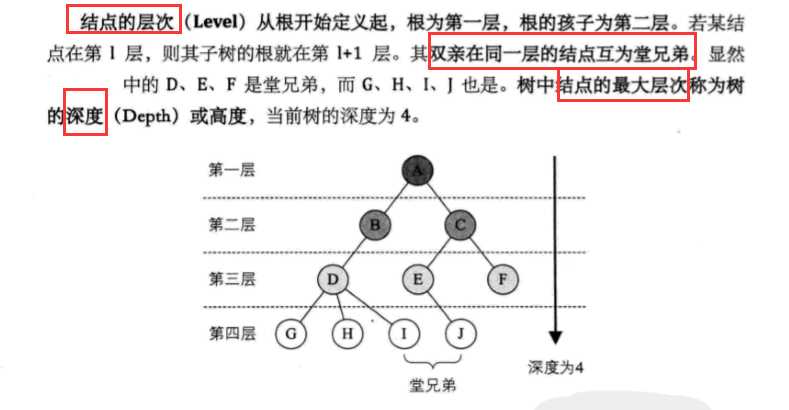
如果将树中结点的各子树看成从左至右是有次序不能互换，则称该树为有序树，否则称为无序树

森林是 m ( m >=  0 ）棵互不相交的树的集合

对树中每个结点而言，其子树的集合即为森林

 

树的抽象数据类型

 

 

树的存储结构

1.双亲表示法

 树中，除了根结点以外，其余每个结点不一定有孩子，但是   一定  有且只有一个双亲

 

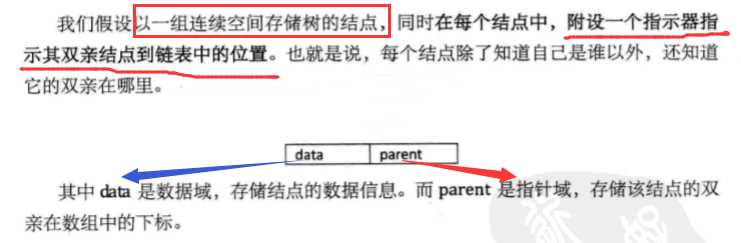
 结构定义代码：

由于根结点是没有双亲的，所以约定位置域设置为-1

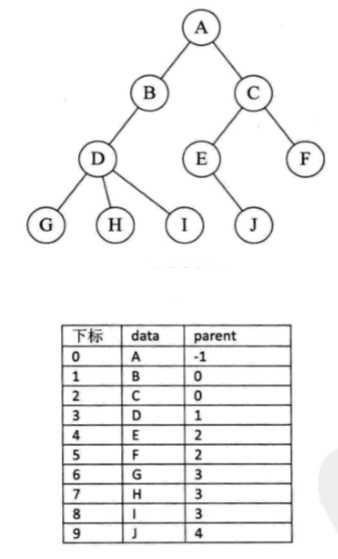
我们可以根据结点的parent指针很容易找到它的双亲结点——> 时间复杂度O（1）

直到parent为-1，表示找到了树节点的根

如果要知道结点的孩子是什么？去遍历吧~

 

 也可以加个长子域、右兄弟域

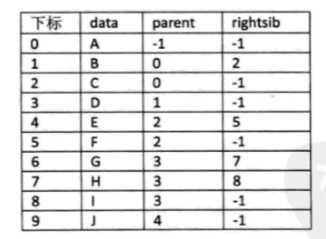
根据需求继续加就行

 

2.孩子表示法

由于树中每个结点可能有多棵子树，可以考虑用多重链表，即每个结点有多个指针域，其中每个指针指向一棵子树的根结点——多重链表表示法

但，树的每个结点的度【即孩子个数】是不同的，所以有两种方案解决：

 

方案一

 指针域的个数 = 树的度

下图树的度是3，所以指针域的个数是3：

——————> 

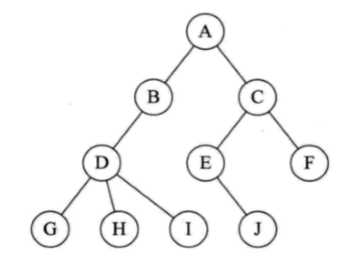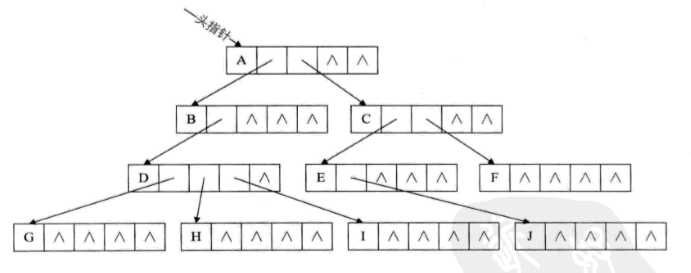
如果树中，各节点的度相差很大——> 浪费空间【因为很多结点的指针域都是空的】

如果相差很小——> 充分利用空间

 

方案二

每个结点的指针域个数 = 该结点的度

对于上方树，其实现方法如下：

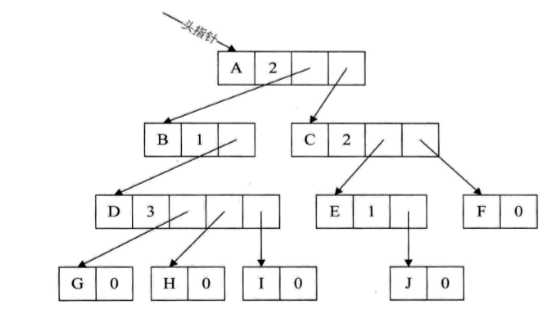
由于各结点的链表是不相同的结构，再加上维护结点的度的数值，运算上回带来时间的损耗

 

更好的方法？

即孩子表示法：

把每个结点的孩子结点排列起来，以单链表作存储结构，则n个结点有n个孩子链表，如果是叶子结点，则此单链表为空

然后，n个头指针又组成一个线性表，采用顺序存储方式，存放进一个而一维数组中

 

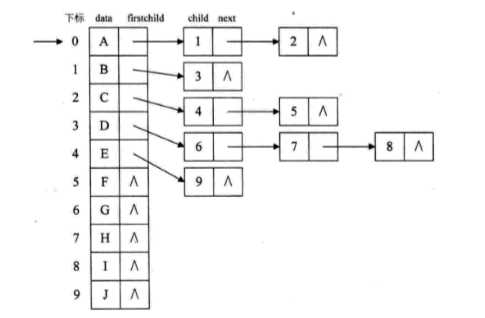
孩子链表的孩子结点结构：

 

 表头数组的表头结点：

结构定义：

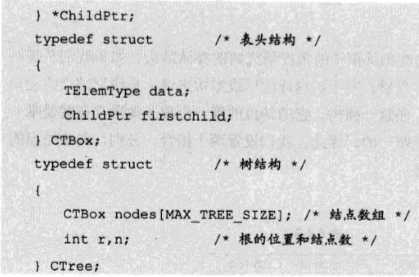
优点：

• 查找某结点的某个孩子、找某结点的兄弟——> 查找结点的孩子链表即可
• 遍历整棵树很方便——> 对头结点的数组循环即可

缺点：

•  找某结点的双亲

 优化——> 双亲孩子表示法

 

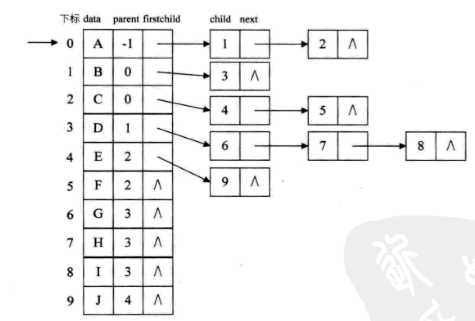
 3.孩子兄弟表示法

 

结构定义代码：

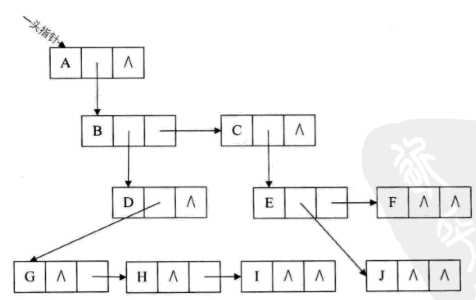
好处：

给查找某个结点的某个孩子带来了方便——> 只需要通过firstchild 找到此结点的长子，再通过长子结点的rightsib 找到它二弟，接着一直下去，直到找到具体的孩子

 

但，找某结点的双亲——> 有缺陷，加个parent指针域即可

 

即，将一棵复杂的树变成了一棵二叉树