线性规划问题复习要点整理

Posted 2021-02-17 aurora-borealis

此处选用的(LP)形式为：

min f = C^Tx ;

s.t.　　AX = b ,

　　　X >= 0,

---

 

1.可行域K != NULL 时，K为第一卦限中的凸多边形，且必存在顶点；

2.最优解存在则必有基本最优解，可行解存在则必存在基本可行解；

3.在求解之前首先观察决策变量定义域，约束条件的格式，若非标准型，则化为标准型；

4.最优条件，由 f(X)=f(X₀)+Σr_jx_j (j 属于I_D)，若r_j>=0，则基本可行解X₀为最优解(若标准型设为 max ，则零r_j<=0即可)；

6.若存在r_i<0，对应y_it<=0，则f无下界，如何求解？设全负列的非基变量为Ε，其余非基变量为0，进行解方程；

7.解判定：

 1）有唯一最优解

　　r_j>0 (j 属于I_D)，>=0；

2）最优解不唯一

　　若最优单纯性表中存在非基变量检验数为0，且对应列向量y^t中存在大于零的元素，则按照最小比值法转轴后，可得另一基本最优解

等价于 https://blog.csdn.net/jiangjieqazwsx/article/details/46701261#commentBox (作者：miangmiang咩) 中提到的，

"假设当前基本可行解是非退化的（即基本可行解的值都严格＞0），若它的基本可行解的所有非基变量的检验数≥0，并存在至少一个等于0，则线性规划问题有无穷多最优解；"

但有一点要注意就是，此时虽然解有无穷多个，但基本最优解只是有限个的

3）解无下界

　　同 6. ；

4）无解,不可行

　　 < 0;　　

8. 若（LP）中基本可行解X的某个基本变量为0，则X是退化的基本可行解，该（LP）为退化的线性规划问题，该问题在进行转轴时可能会发生无穷的迭代，导致死循环的产生，如何解决？可利用 Bland‘s Law 来确定转轴指标t和k，以避免出现死循环；

9.单纯性表的矩阵描述，

Y=B^-1A

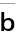=B^-1b

r=C-C_B^Tb

f₀=C_B^TB^-1b

10.大M法和两阶段法

1）大M法

　　大M法是来解决初始基变量选择的问题的，用无穷大的M和值为0的x对表达式进行补充，其求解与一般单纯性表的求解一样，结果若在最后的单纯性表中，基变量还存在着值大于0的人工变量，则（LP）不可行；繁殖，若人工变量的之都为零则（LP）和（LPM）都有最优解或无下界；

2）两阶段法

　　两阶段的应用背景是对计算机无法使用的大M法情况下的另一种求解方式，在求（LP）之前先求（LP1）,（LP1）的目标函数是引进的人工变量的和（注意人工变量、松弛变量、剩余变量的区别），用单纯性法求求最优值，得到（LP）问题的基变量和最优解，删去人工变量列，重新计算检验数r和f₀（注意单纯性表中的最优值显示的是‘w= -f₀’）

11.线性规划问题可能出现约束之间线性相关的情况，可以在解答开始检查一下并删去相应约束，使之线性无关，或者在用单纯形法的过程中发现某一行所有目标函数变量的值都为0了，对应的b也为0了，这是可以删掉该行，和对应基变量的列；

ok，第一章复习到这了