The Preliminary Contest for ICPC China Nanchang National Invitational and International Silk-Road Pr

Posted 2021-02-17 cmyg

 

打网络赛

比赛前的准备工作要做好

确保 c++/java/python的编译器能用

打好模板，放在桌面

 

A. PERFECT NUMBER PROBLEM

 1 #include <cstdio>
 2 #include <cstdlib>
 3 #include <cmath>
 4 #include <cstring>
 5 #include <string>
 6 #include <algorithm>
 7 #include <set>
 8 #include <map>
 9 #include <queue>
10 #include <iostream>
11 using namespace std;
12 
13 #define ll long long
14 
15 const int maxn=1e8+10;
16 const int inf=1e9;
17 const double eps=1e-8;
18 
19 int sum[maxn];
20 
21 int main()
22 {
23     int n=100000000,i,j;
24     for (i=1;i<n;i++)
25         for (j=i;j<n;j+=i)
26             sum[j]+=i;
27     for (i=1;i<n;i++)
28         if (sum[i]==i+i)
29             printf("%d ",i);
30     return 0;
31 }
32 /*
33 6 28 496 8128 33550336
34 Process returned 0 (0x0)   execution time : 24.646 s
35 */

 

较差的打表方法

 1 #include <cstdio>
 2 #include <cstdlib>
 3 #include <cmath>
 4 #include <cstring>
 5 #include <string>
 6 #include <algorithm>
 7 #include <set>
 8 #include <map>
 9 #include <queue>
10 #include <iostream>
11 using namespace std;
12 
13 #define ll long long
14 
15 const int maxn=1e4+10;
16 const int inf=1e9;
17 const double eps=1e-8;
18 
19 
20 
21 int main()
22 {
23     ///我相信很大一部分同学是网上找答案的，这不好
24 //    printf("6
28
496
8128
33550336");
25     ll sum,i,j,k;
26     for (i=1;i<=1000000000;i++)
27     {
28         sum=0;
29         k=sqrt(i);
30         for (j=1;j<=k;j++)
31             if (i%j==0)
32                 sum+=j+i/j;
33         if (k*k==i)
34             sum-=i;
35         sum-=i;
36         if (sum==i)
37             printf("%d ",i);
38         if (i%1000000==0)
39             printf("i=%d
",i);
40     }
41     return 0;
42 }
43 /*
44 6 28 496 8128 33550336
45 18 min
46 */

 

C. Angry FFF Party

fib(x) 逐渐变得很大

而fib(fib(x))更是如此，

感觉可以打表

于是用python打表验证一下

 1 import math
 2 
 3 ?
 4 
 5 a=1/math.sqrt(5)
 6 
 7 b=(1+math.sqrt(5))/2
 8 
 9 c=(1-math.sqrt(5))/2
10 
11 a
12 
13 0.4472135954999579
14 
15 a
16 
17 for n in range(1,16):
18 
19     print(n)
20 
21     x=a*(pow(b,n) - pow(c,n))
22 
23     x=round(x)
24 
25     print(x)
26 
27 ?
28 
29     y=a*(pow(b,x) - pow(c,x))
30 
31     print(y)
32 
33     print()
34 
35 1
36 1
37 1.0
38 
39 2
40 1
41 1.0
42 
43 3
44 2
45 1.0
46 
47 4
48 3
49 2.0
50 
51 5
52 5
53 5.000000000000001
54 
55 6
56 8
57 21.000000000000004
58 
59 7
60 13
61 233.00000000000006
62 
63 8
64 21
65 10946.000000000007
66 
67 9
68 34
69 5702887.0000000065
70 
71 10
72 55
73 139583862445.00024
74 
75 11
76 89
77 1.7799794160047194e+18
78 
79 12
80 144
81 5.555654042242954e+29
82 
83 13
84 233
85 2.2112364063039317e+48
86 
87 14
88 377
89 2.746979206949977e+78
90 
91 15
92 610
93 1.3582369791278544e+127

 

开始用java写 BigInteger

  1 import java.math.BigInteger;
  2 import java.util.Scanner;
  3 
  4 public class Main {
  5     static class mat {
  6         BigInteger [][]a=new BigInteger[2][2];
  7         mat() {
  8             a[0][0]=a[0][1]=a[1][0]=a[1][1]=BigInteger.ZERO;
  9         }
 10         static mat mul(mat a,mat b) {
 11             mat c=new mat();
 12             for (int k=0;k<2;k++)
 13                 for (int i=0;i<2;i++)
 14                     for (int j=0;j<2;j++)
 15                         c.a[i][j]=c.a[i][j].add(a.a[i][k].multiply(b.a[k][j]));
 16             return c;
 17         }
 18         void print() {
 19             for (int i=0;i<2;i++) {
 20                 for (int j=0;j<2;j++)
 21                     System.out.print(a[i][j]+" ");
 22                 System.out.println();
 23             }
 24             System.out.println();
 25         }
 26     }
 27     
 28     static BigInteger _pow(int n) {
 29         mat a=new mat();
 30         mat b=new mat();
 31         a.a[0][0]=BigInteger.ONE;
 32         a.a[0][1]=BigInteger.ZERO;
 33         a.a[1][0]=BigInteger.ZERO;
 34         a.a[1][1]=BigInteger.ONE;
 35         
 36         b.a[0][0]=BigInteger.ONE;
 37         b.a[0][1]=BigInteger.ONE;
 38         b.a[1][0]=BigInteger.ONE;
 39         b.a[1][1]=BigInteger.ZERO;
 40 
 41         while (n>0) {
 42             if (n%2==1)
 43                 a=mat.mul(a,b);
 44             b=mat.mul(b,b);
 45 //            b.print();
 46             n>>=1;
 47         }
 48         return a.a[1][0];
 49     }
 50     
 51     public static void main(String[] args) throws Exception {
 52         
 53         int i,len=100000;//10
 54         int []a=new int[100];
 55         BigInteger []b=new BigInteger[100];
 56         StringBuffer s=new StringBuffer("1");
 57         for (i=0;i<len;i++)
 58             s=s.append("0");
 59         String ss=new String(s);
 60         BigInteger maxb=new BigInteger(ss);
 61 //        System.out.println(maxb);
 62         
 63 //        _pow(10);
 64         
 65         a[1]=a[2]=1;
 66         mat ma = new mat();
 67         for (i=1;i<100;i++) {
 68             if (i<3)
 69                 a[i]=1;
 70             else
 71                 a[i]=a[i-1]+a[i-2];
 72 //            System.out.println(a[i]);
 73             b[i]=_pow(a[i]);
 74 //            if (i<10)
 75 //                System.out.println(b[i]);
 76             if (b[i].compareTo(maxb)>=0)
 77                 break;
 78         }
 79 //        System.out.println("i="+i);
 80         int maxg=i;
 81         
 82         Scanner in=new Scanner(System.in);
 83         int t=in.nextInt();
 84         BigInteger m;
 85         
 86         int []num=new int[100];
 87             int g=0;
 88             BigInteger[] bb=new BigInteger[11];
 89             for (i=0;i<=10;i++)
 90                 bb[i]=new BigInteger(Integer.toString(i));
 91             String []pr=new String[11];
 92             
 93         /*
 94         1 1 1 2 5 21
 95         */
 96             pr[1]="1";
 97             pr[2]="1 2";
 98             pr[3]="1 2 3";
 99             pr[4]="1 2 4";
100             pr[5]="1 2 3 4";
101             for (i=6;i<=10;i++)
102                 pr[i]=pr[i-5]+" 5";
103             
104         while (t-->0) {
105             m=in.nextBigInteger();
106             
107             g=0;
108             if (m.compareTo(bb[10])>0) {
109                 for (i=maxg;i>5;i--)
110                     if (m.compareTo(b[i])>=0) {
111                         m=m.subtract(b[i]);
112                         g=g+1;
113                         num[g]=i;
114                     }
115             }
116             if (m.compareTo(bb[10])>0)
117                 System.out.println(-1);
118             else {                
119                 for (i=1;i<=10;i++)
120                     if (m.compareTo(bb[i])==0)
121                         System.out.print(pr[i]);
122                 if (m.compareTo(bb[0])!=0 && g!=0)
123                     System.out.print(" ");
124                 if (g==0)
125                     System.out.println();
126                 for (i=g;i>=1;i--) {
127                     System.out.print(num[i]);
128                     if (i==1)
129                         System.out.println();
130                     else
131                         System.out.print(" ");
132                 }
133             }
134         }
135     }
136 }
137 /*
138 1 1 1 2 5 21
139 
140 1
141 1
142 1
143 2
144 5
145 21
146 233
147 10946
148 5702887
149 
150 100
151 1-10
152 11
153 21
154 27
155 */

 

H. Coloring Game

 

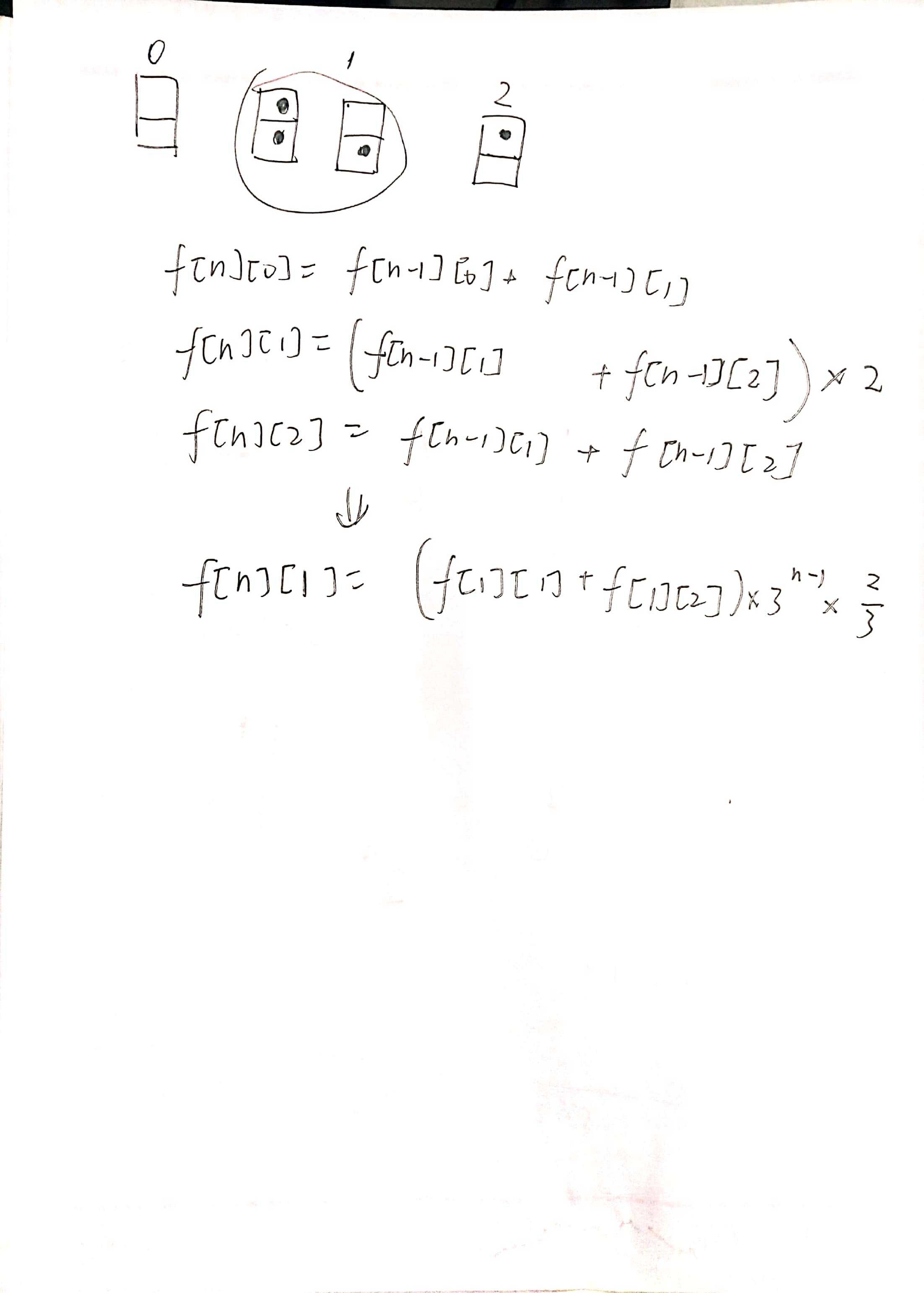
 1 #include <cstdio>
 2 #include <cstdlib>
 3 #include <cmath>
 4 #include <cstring>
 5 #include <string>
 6 #include <algorithm>
 7 #include <set>
 8 #include <map>
 9 #include <queue>
10 #include <iostream>
11 using namespace std;
12 
13 #define ll long long
14 
15 const int maxn=1e4+10;
16 const int inf=1e9;
17 const double eps=1e-8;
18 const ll mod=1e9+7;
19 
20 ll mul(ll a,ll b)
21 {
22     ll y=1;
23     while (b)
24     {
25         if (b&1)
26             y=y*a%mod;
27         a=a*a%mod;
28         b>>=1;
29     }
30     return y;
31 }
32 
33 int main()
34 {
35     int n;
36     scanf("%d",&n);
37     if (n==1)
38         printf("1");
39     else
40         printf("%lld",mul(3,n-2)*4%mod);
41     return 0;
42 }
43 /*
44 1000000000
45 */

 

K. MORE XOR

找规律

推公式较为复杂，据说用插板法

#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <string>
#include <algorithm>
#include <set>
#include <map>
#include <queue>
#include <iostream>
using namespace std;

#define ll long long

const int maxn=1e5+10;
const int inf=1e9;
const double eps=1e-8;

int f[4][maxn],a[maxn];

int main()
{
//    printf("%d",1^2^5^6^9^10);
    int T,n,q,i,j,k,x,y,s,t,v;
    scanf("%d",&T);
    while (T--)
    {
        scanf("%d",&n);
        for (i=1;i<=n;i++)
            scanf("%d",&a[i]);

        for (k=0;k<4;k++)
            for (i=(k==0)?4:k,j=1;i<=n;i+=4,j++)
                f[k][j]=f[k][j-1]^a[i];

        scanf("%d",&q);
        while (q--)
        {
            scanf("%d%d",&i,&j);
            y=(j-i+1)%4;
            if (y==1)
            {
                ///i,i+4,i+8 ...
                x=i%4;
                s=(i+3)/4;
                t=s+(j-i)/4;
                printf("%d
",f[x][t]^f[x][s-1]);
            }
            else if (y==2)
            {
                x=i%4;
                s=(i+3)/4;
                t=s+(j-i)/4;
                v=f[x][t]^f[x][s-1];

                i++;
                x=i%4;
                s=(i+3)/4;
                t=s+(j-i)/4;
                printf("%d
",v^f[x][t]^f[x][s-1]);
            }
            else if (y==3)
            {
                i++;
                x=i%4;
                s=(i+3)/4;
                t=s+(j-i)/4;
                printf("%d
",f[x][t]^f[x][s-1]);
            }
            else
                printf("0
");
        }
    }
    return 0;
}
/*
1
10
1 2 3 4 5 6 7 8 9 10
100
1 7
*/

 

 1 #include <cstdio>
 2 #include <cstdlib>
 3 #include <cmath>
 4 #include <cstring>
 5 #include <string>
 6 #include <algorithm>
 7 #include <set>
 8 #include <map>
 9 #include <queue>
10 #include <iostream>
11 using namespace std;
12 
13 #define ll long long
14 
15 const int maxn=1e4+10;
16 const int inf=1e9;
17 const double eps=1e-8;
18 
19 int n=10;
20 
21 struct node
22 {
23     int a[30];
24     node operator+(const node &y)
25     {
26         node z;
27         for (int i=1;i<=n;i++)
28             z.a[i]=a[i]+y.a[i];
29         return z;
30     }
31 }f[4][30][30];
32 
33 int main()
34 {
35     int i,j,k,l;
36     int x=3;
37     for (i=1;i<=n;i++)
38         f[0][i][i].a[i]=1;
39     for (l=1;l<=x;l++)
40     {
41 //        for (i=1;i<n;i++)
42 //        {
43 //            f[l][i][i]=f[l-1][i][i];
44 //            for (j=i+1;j<=n;j++)
45 //                f[l][i][j]=f[l][i][j-1]+f[l-1][j][j];
46 //        }
47 
48         for (i=1;i<=n;i++)
49             for (j=i;j<=n;j++)
50             {
51                 if (i!=j)
52                     f[l][i][j]=f[l][i][j-1];
53                 for (k=i;k<=j;k++)
54                     f[l][i][j]=f[l][i][j]+f[l-1][k][j];
55             }
56     }
57     int y=3;
58     for (i=1;i<=n;i++)
59     {
60         for (j=1;j<=n;j++)
61 //            printf("%d%c",f[y][1][i].a[j],j==n?‘
‘:‘ ‘);
62             printf("%d%c",f[y][1][i].a[j] &1,j==n?‘
‘:‘ ‘);
63     }
64     return 0;
65 }
66 /*
67 1 0 0 0 0 0 0 0 0 0
68 1 1 0 0 0 0 0 0 0 0
69 0 1 0 0 0 0 0 0 0 0
70 0 0 0 0 0 0 0 0 0 0
71 1 0 0 0 1 0 0 0 0 0
72 1 1 0 0 1 1 0 0 0 0
73 0 1 0 0 0 1 0 0 0 0
74 0 0 0 0 0 0 0 0 0 0
75 1 0 0 0 1 0 0 0 1 0
76 1 1 0 0 1 1 0 0 1 1
77 
78 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
79 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
80 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
81 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
82 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
83 1 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
84 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
85 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
86 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
87 1 1 0 0 1 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0
88 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0
89 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
90 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0
91 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 0 0 0 0
92 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0
93 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
94 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0
95 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0
96 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0
97 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
98 */

 

 

M. Subsequence

dp

 1 #include <cstdio>
 2 #include <cstdlib>
 3 #include <cmath>
 4 #include <cstring>
 5 #include <string>
 6 #include <algorithm>
 7 #include <set>
 8 #include <map>
 9 #include <queue>
10 #include <iostream>
11 using namespace std;
12 
13 #define ll long long
14 
15 const int maxn=1e5+10;
16 const int inf=1e9;
17 const double eps=1e-8;
18 
19 int f[maxn][128],pre[maxn];
20 char s[maxn];
21 
22 int main()
23 {
24     int i,j,len,t;
25     memset(pre,0xff,sizeof(pre));
26     s[0]=‘a‘;
27     scanf("%s",s+1);
28     len=strlen(s+1);
29     for (i=len;i>=0;i--)
30     {
31         for (j=0;j<128;j++)
32             f[i][j]=pre[j];
33         pre[s[i]]=i;
34     }
35     scanf("%d",&t);
36     while (t--)
37     {
38         scanf("%s",s);
39         len=strlen(s);
40         j=f[0][s[0]];
41         for (i=1;i<len;i++)
42         {
43             if (j==-1)
44                 break;
45             j=f[j][s[i]];
46         }
47         if (j!=-1)
48             printf("YES
");
49         else
50             printf("NO
");
51     }
52     return 0;
53 }
54 /*
55 
56 */

 

C. Angry FFF Party

数位dp

原来的数据是完全无用的，
只需要火柴棒总数保持一致，
只需要对于每一位，火柴棒加的次数完全一样

不用考虑前导0
+0 -> +9
-0  -> +5

w为数字的位数，y使用的火柴数
f[w][y] 的最大值
f[w][y]=max(f[w-1][y-g[i]]+i*10^(w-1))    i=0..9
w<10,y<w*7+2

-11..1 无法改变
f[1][3]=-1
f[p][p*2+1]=-11..1
其它时候不用减法(至少可以节省一根火柴，使负号变为加号)
这个不成立，在第一个数时(潜在加法)
预处理

对于当前的前x个数字，y为使用的火柴棒总数，以此最大的值
对于第x个数字，位数为w
a[x][y]=max(a[x-1][z]+f[w][z-y])
x<=50,y<=7*50+2*49=448
[49个加号，50个数]


易错点：
+/- 不能单独每一位，而要整体求

 

正确通过

2019-04-21 00:57

5ms

448kB

c++14

  1 #include <cstdio>
  2 #include <cstdlib>
  3 #include <cmath>
  4 #include <cstring>
  5 #include <string>
  6 #include <algorithm>
  7 #include <set>
  8 #include <map>
  9 #include <queue>
 10 #include <iostream>
 11 using namespace std;
 12 
 13 #define ll long long
 14 
 15 const int maxn=1e4+10;
 16 const int inf=1e9;
 17 const double eps=1e-8;
 18 
 19 /**
 20 其实最多只有9位，
 21 是小于10^9，没有等于
 22 
 23 999999999+999999999+...
 24 超过int
 25 **/
 26 
 27 int g[10]={6,2,5,5,4,5,6,3,7,6};
 28 int f[12][100];
 29 int mul[12];
 30 ll a[51][500];
 31 int fv[12];
 32 int add[128];
 33 char s[110];
 34 
 35 int main()
 36 {
 37     bool vis;
 38     int i,j,k,l,maxw,w,t,n,tot,sum,c;
 39 
 40 //    printf("%d
",‘+‘);///43
 41 //    printf("%d
",‘-‘);///45
 42     add[43]=2,add[45]=1;
 43     for (i=48;i<48+10;i++)
 44         add[i]=g[i-48];
 45 
 46     mul[1]=1;
 47     for (i=2;i<=9;i++)
 48         mul[i]=mul[i-1]*10;
 49 
 50     fv[1]=-1;
 51     for (i=2;i<=9;i++)
 52         fv[i]=fv[i-1]*10-1;
 53 
 54     memset(f,0x8f,sizeof(f));
 55     f[0][2]=0;///+
 56     for (i=1;i<=10;i++)
 57     {
 58         maxw=(i-1)*7+2;
 59         for (j=0;j<=maxw;j++)
 60             for (l=0;l<=9;l++)  ///或者只要用火柴数在一个数量时最大的数即可
 61                 f[i][j+g[l]]=max(f[i][j+g[l]],f[i-1][j]+l*mul[i]);
 62     }
 63 
 64     scanf("%d",&t);
 65     while (t--)
 66     {
 67         memset(a,0x8f,sizeof(a));
 68         scanf("%d",&n);
 69         scanf("%s",s);
 70         tot=0;
 71         vis=0;
 72         sum=0;
 73         a[0][0]=0;
 74         i=0;
 75         c=0;
 76         for (w=0;w<=n;w++)
 77         {
 78             tot+=add[s[w]];
 79             if (s[w]==‘+‘ || s[w]==‘-‘ || w==n)
 80             {
 81                 c++;
 82                 maxw=i*7+2;
 83                 for (j=0;j<=sum;j++)
 84                     for (k=0;k<=maxw;k++)
 85                         ///f[i][k](int memset)相比a[j](ll memset)小很多，减很多次，仍不会到达下界
 86                         a[c][j+k]=max(a[c][j+k],a[c-1][j]+f[i][k]); ///可以使用滚动数组
 87 
 88                 if (vis)
 89                     for (j=0;j<=sum;j++)
 90                         a[c][j+2*i+1]=max(a[c][j+2*i+1],a[c-1][j]+fv[i]);
 91 
 92                 sum+=maxw; ///当然也可以求出tot后再求
 93                 vis=1;
 94                 i=0;
 95                 continue;
 96             }
 97             else
 98                 i++;
 99         }
100         printf("%lld
",a[c][tot+2]);  ///第一个加号是没有的
101     }
102     return 0;
103 }
104 /*
105 10
106 11
107 100000000+9
108 13
109 111-111111-11
110 20
111 100000000-99999999+1
112 36
113 10000000+12345+0+1+2+3+4+5+6+7+8+9
114 
115 */

 

 

未完待续

I. Max answer

 

J. Distance on the tree