LAD 线性判别分析

Posted 2021-02-17 yanshw

线性判别分析，简称LDA，是一种线性学习方法。

常用来降维，是一种有监督的降维方法，是基于最佳分类效果的降维方法。

 

核心思想

给定训练样本，带label，设法将样本投影到一条直线上，使得同类样例的投影尽可能接近，异类样例的投影尽可能远离；

在对新样本进行预测时，先将其投影到这条直线上，再根据投影点的位置确定类别。

 

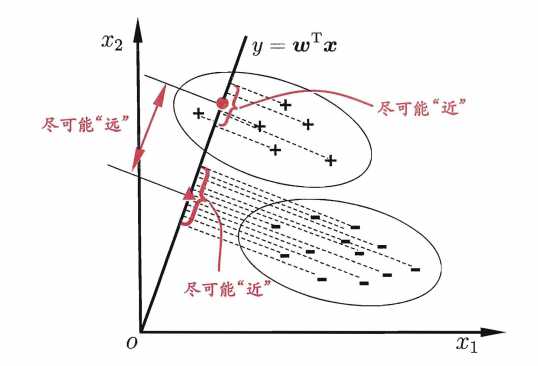
以二分类为例，x1  x2 代表训练集，u1 u2 代表样本均值，cov1 cov2 代表样本协方差矩阵，将样本投影到直线w上，则两样本的中心的投影分别为 wu1  wu2，两样本的协方差为 w^Tcov1w  w^Tcov2w ，

要使同类间距离尽可能小，需使 w^Tcov1w + w^Tcov2w 尽可能小；

要使异类间距离尽可能大，需使 |wu1-wu2| 尽可能大，

综合考虑，则可得到如下式子

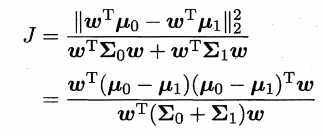
目标是使得 J 最大。

 

具体求解过程省略，实际应用中一般不会自己实现LDA，因为LDA只是算法中很小的一个步骤，而其本身求解比较麻烦。

class sklearn.lda.LDA(solver=‘svd‘, shrinkage=None, priors=None, n_components=None, store_covariance=False, tol=0.0001)

 

示例代码

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(iris.data,iris.target)
X_new = lda.transform(iris.data)
print(X_new)

上面写了两个接口，适用不同版本。

 

LDA与PCA的应用场景对比

若两类样本的均值有明显差异，LDA较优

 

若两类样本均值无明显差异，但协方差差异很大，PCA较优

 

在实际应用中也常结合LDA和PCA一起使用，先用PCA降维消除噪声，再用LDA降维。

 

 

参考资料：

周志华《机器学习》

https://mp.weixin.qq.com/s?__biz=MzU0MDQ1NjAzNg==&mid=100002594&idx=1&sn=c9cdfc2c174ae6f4a36b383439a1627a&chksm=7b39ae294c4e273ff314dee92d2fff280ba7aa9ff74ae9f2a8f0345d8e794f30dfd2c9d4f9d4#rd

https://scikit-learn.org/0.16/modules/generated/sklearn.lda.LDA.html