科学计算和可视化

Posted 2021-02-17 iconangle

今天的主题是有关科学计算和可视化的，其中将会包括有python的第三方库numpy以及matplotlib的学习总结及应用！

有所涉猎的同学一定对这两个库并不陌生！它们分别是对数组的处理和数据处理的图表制作工具，在数据处理方面它们都有不俗的表现！

接下来先让我简单介绍一下这两个库~（安装过程就不详述啦~pip install +库就能随心安装，或者你也可以选择直接安装Anaconda 强大的库函数多到你用不完，里面自然有今天所要展开了解的两个库啦~）

numpy:

概述：numpy（Numerical Python）提供了python对多维数组对象的支持：ndarray，具有矢量运算能力，快速、节省空间。numpy支持高级大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库，它在数据处理方面有它不俗的表现力。

创建ndarray数组：ndarray：N维数组对象（矩阵），所有元素必须是相同类型。 
ndarray属性：ndim属性，表示维度个数；shape属性，表示各维度大小；dtype属性，表示数据类型。

一些函数汇总：

函数	说明
array	将输入数据（列表、元组、数组或其他序列类型）转换为ndarray、要么推断出dtype，要么显示指定dtpye。默认直接复制输入数据
asarray	将输入转换为ndarray，如果输入本身就是一个ndarray将不进行复制
arange	类似于内置的range，但返回的是一个ndarray而不是列表
ones、ones_like	根据指定的形状和dtpye创建一个全1的数组。ones_like以另一个数组为参数，并根据其形状和dtype创建一个全1的数组
zeros、zeros_like	类似上一项，创建全为0的数组
empty、empty_like	创建新数组，只分配内存空间但不填充任何值
eye、identity	创建一个正方的N*N单位矩阵（对角线为1，其余为0）

 

 

 

 

 

 

 

 

 

当然还有一些通用函数，比如说我们的math库中的一些计算函数fabs,abs,sqrt,sin,cos等等，这些同样适合于ndarray，这里就不一一列举了。

现在来看看我们的实例应用吧~

实验一：

import numpy
print (‘使用列表生成一维数组‘)
data = [1,2,3,4,5]
x = numpy.array(data)
print (x) 
print (x.dtype)
print (x.ndim) 
print (x.shape)

print (‘使用列表生成二维数组‘)
data = [[1,0],[2,0],[3,0]]
x = numpy.array(data)
print (x) 
print (x.ndim) 
print (x.shape)

print (‘使用zero/ones/empty创建数组:根据shape来创建‘)
x = numpy.zeros(5)
print (x)
x = numpy.zeros((3,3))
print (x)
x = numpy.ones((2,3))
print (x)
x = numpy.empty((3,2))
print (x)

print (‘使用arrange生成连续元素‘)
print (numpy.arange(5))
print (numpy.arange(0,5,2))

效果：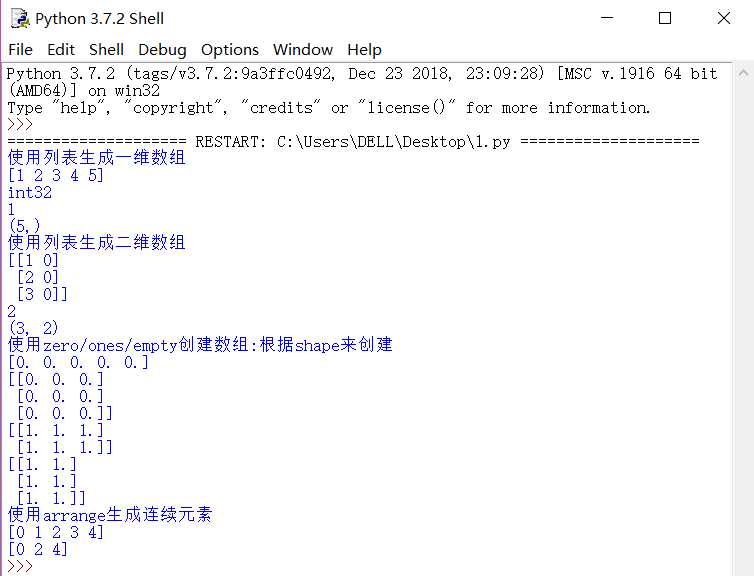

我们看到这个试验中我们新建了一些特殊数组（单位数组即全1数组，全0数组，以及一、二维数组，当然还有其中各元素的type(类型)的讨论）

我们还可以学习到numpy中的ndarray的数据类型，有大致下面几种：

类型	类型代码	说明
int8、uint8	i1、u1	有符号或无符号的8位（1个字节）整型
int16、uint16	i2、u2	有符号或无符号的16位（2个字节）整型
int32、uint32	i4、u4	有符号或无符号的32位（4个字节）整型
int64、uint64	i8、u8	有符号或无符号的64位（8个字节）整型
float16	f2	半精度浮点数
float32	f4/f	标准的单精度浮点数。与C的float兼容
float64	f8/d	标准的双精度浮点数。与C的double和python的float对象兼容
float128	f16/g	扩展精度浮点数
complex64、complex128	c8/c16	分别用两个32位、64位或128位的浮点数表示复数
complex256	c32	复数
bool	?	储存True和False值的布尔类型
object	O	python对象类型
string_	S	固定长度的字符串类型（每个字符1个字符）S10即为创建长度为10的字符串
unicode_	U	固定长度的unicode类型（字节数由平台决定）U10即为创建长度为10的unicode

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

实验二：

import numpy

print (‘生成指定元素类型的数组:设置dtype属性‘)
x = numpy.array([1,2.6,3],dtype = numpy.int64)
print (x) 
print (x.dtype)
print (x.ndim) 
print (x.shape)
x = numpy.array([1,2,3],dtype = numpy.float64)
print (x) 
print (x.dtype)
print (x.ndim) 
print (x.shape)
x = numpy.array([-1,-2,-3,-4],dtype = numpy.uint16)
print (x) 
print (x.dtype)
print (x.ndim) 
print (x.shape)

print (‘使用astype复制数组，并转换类型‘)
x = numpy.array([1,2.6,3],dtype = numpy.float64)
y = x.astype(numpy.int32)
print (y)
print (x)
print (x.ndim) 
print (x.shape)
z = y.astype(numpy.float64)
print (z)
print (x.ndim) 
print (x.shape)

print (‘将字符串元素转换为数值元素‘)
x = numpy.array([‘1‘,‘2‘,‘3‘],dtype = numpy.string_)
y = x.astype(numpy.int32)
print (x)
print (x.ndim) 
print (x.shape)
print (y)

print (‘使用其他数组的数据类型作为参数‘)
x = numpy.array([ 1., 2.6,3. ],dtype = numpy.float32)
y = numpy.arange(3,dtype=numpy.int32)
print (y)
print (y.astype(x.dtype))

效果：

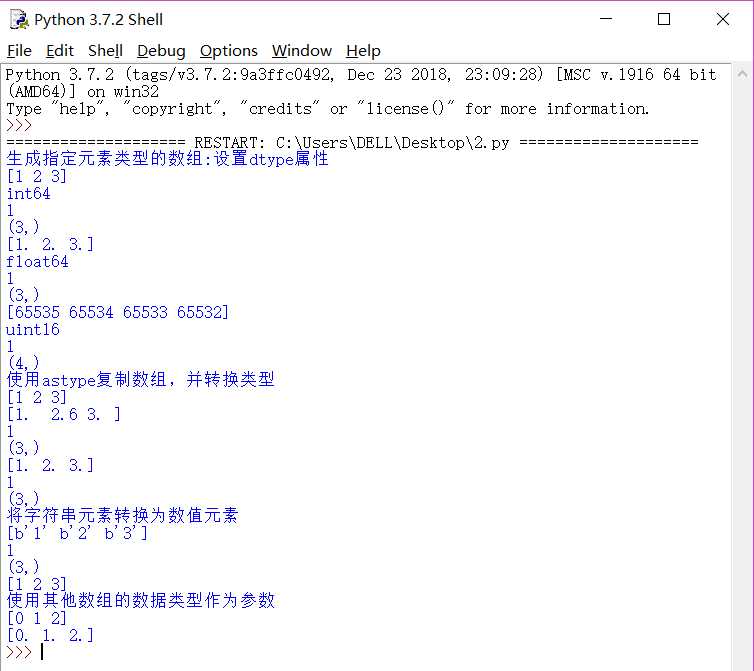
在这个实验中，我们具体讨论了数组的不同数据类型的情况下生成数据的例子，我们尝试了int,float,和uint三种形式，得到了想要的结果（其中我们知道uint是无符号整型，它在计算机内存中一其相对应正数的补码形式存在，故会出现上述情况，-1的补码是1111 1111，值为10进制数为65535）我们还对dtype属性进行讨论，尝试了复制其属性的功能……

实验三：

import numpy
print (‘ndarray数组与标量/数组的运算‘)
x = numpy.array([1,2,3]) 
print (x*2)
print (x**2)
print (x>2)
y = numpy.array([3,4,5])
print (x+y)
print (x^y)
print (x>y)

print (‘ndarray的花式索引:使用整型数组作为索引‘)
x = numpy.array([1,2,3,4,5,6])
print (x[[0,1,2]])
print (x[[-1,-2,-3]])
x = numpy.array([[1,2],[3,4],[5,6]])
print (x[[0,1]])
print (x[[0,1],[0,1]]) # [1,4] 打印x[0][0]和x[1][1]
print (x[[0,1]][:,[0,1]]) # 打印01行的01列 [[1,2],[3,4]]
# 使用numpy.ix_()函数增强可读性
print (x[numpy.ix_([0,1],[0,1])]) 
x[[0,1],[0,1]] = [0,0]
print (x)# [[0,2],[3,0],[5,6]]

效果：

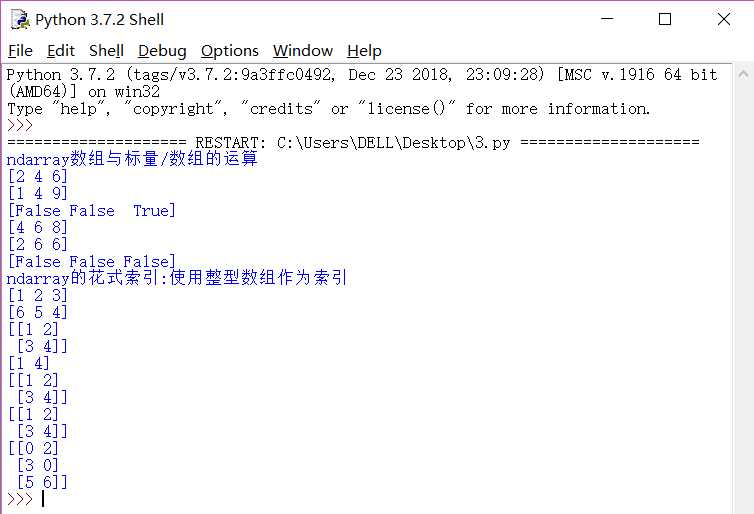
该例有数组之间的简单的数乘运算以及bool运算和花式索引的实现~

实验四：

import numpy
print (‘ndarray数组的转置和轴对换‘)
k = numpy.arange(9)
m = k.reshape((3,3)) # 改变数组的shape复制生成2维的，每个维度长度为3的数组
print (k)
print (m)
# 转置(矩阵)数组：T属性 : mT[x][y] = m[y][x]
print (m.T)
# 计算矩阵的内积 xTx
print (numpy.dot(m,m.T)) # numpy.dot点乘
# 高维数组的轴对象
k = numpy.arange(8).reshape(2,2,2)
print (k)
print (k[1][0][0])
# 轴变换 transpose 参数:由轴编号组成的元组
m = k.transpose((1,0,2))
print (m)
print (m[0][1][0])
# 轴交换 swapaxes (axes：轴)，参数:一对轴编号
m = k.swapaxes(0,1)
print (m)
print (m[0][1][0])
# 使用轴交换进行数组矩阵转置
m = numpy.arange(9).reshape((3,3))
print (m)
print (m.swapaxes(1,0))

效果：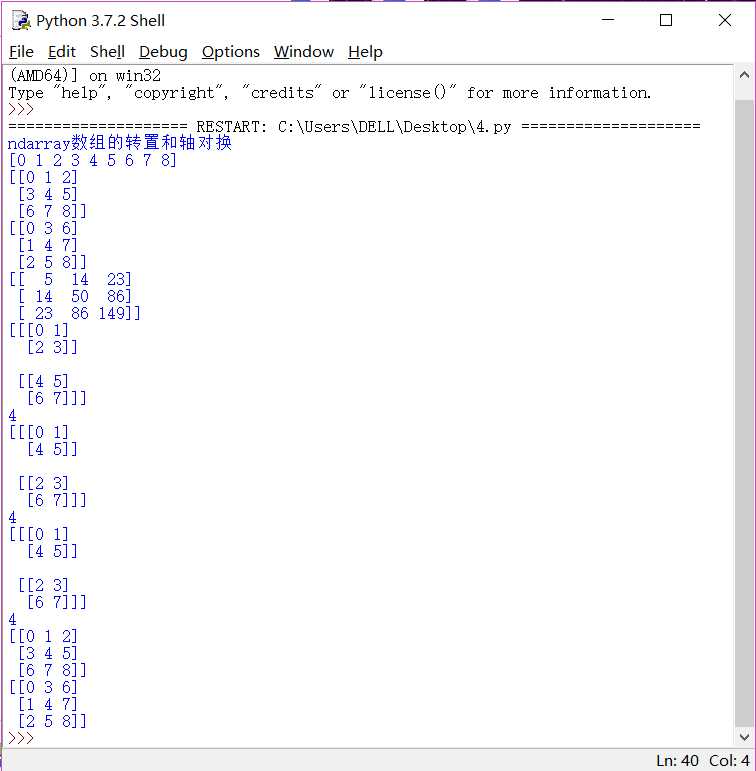

该例，就是有关数列或说矩阵的基本运算（数乘运算，转置，点乘等）……

学习了这些numpy库已经在日常中基本够用，当然它还有很多值得探讨深挖的部分，上述只是冰山一角哦~当然不要忘了多加练习！！

matplotlib:

概述：matplotlib是基于numpy的一套Python工具包。这个包提供了丰富的数据绘图工具，主要用于绘制一些统计图形。

在这个强大的库的学习过程中，我得到了一个非常有用的消息：IPython的使用，特别在matplotlib的运用中，这个环境下的表现出乎意料的好！不禁感叹聪明的计算机工程师大触们的才智之高！

那么如何使用IPython库呢？

一样用cmd命令行，利用指令"ipython --pylab"就可以调用出IPython环境：

然后输入代码（从网上copy并稍作修改）：

效果：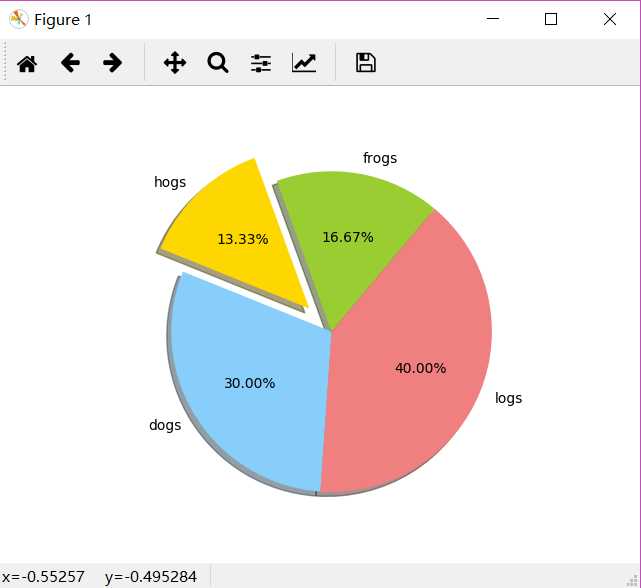

非常nice的效果，直观又美观！matplotlib实在是作图做表神器！

matplotlib参数设置：

在代码执行过程中，有两种方式更改参数：

• 使用参数字典(rcParams)
• 调用matplotlib.rc()命令 通过传入关键字元组，修改参数

axex: 设置坐标轴边界和表面的颜色、坐标刻度值大小和网格的显示
backend: 设置目标暑促TkAgg和GTKAgg
figure: 控制dpi、边界颜色、图形大小、和子区( subplot)设置
font: 字体集（font family）、字体大小和样式设置
grid: 设置网格颜色和线性
legend: 设置图例和其中的文本的显示
line: 设置线条（颜色、线型、宽度等）和标记
patch: 是填充2D空间的图形对象，如多边形和圆。控制线宽、颜色和抗锯齿设置等。
savefig: 可以对保存的图形进行单独设置。例如，设置渲染的文件的背景为白色。
verbose: 设置matplotlib在执行期间信息输出，如silent、helpful、debug和debug-annoying。
xticks和yticks: 为x,y轴的主刻度和次刻度设置颜色、大小、方向，以及标签大小。

作为中国程序员，在面向中国人群体时，我们在制作图表的过程中免不了会使用中文标注，分析等，那要怎么加中文字呢？
我们会使用：

import matplotlib.pyplot as plt
plt.rcParams[‘font.family‘]=[‘SimHei‘] #用来正常显示中文标签
plt.rcParams[‘axes.unicode_minus‘]=False #用来正常显示负号

还是刚刚的代码，加了中文的“SimHei”（黑体）显示，可以有下面的表现形式：

import matplotlib.pyplot as plt
plt.rcParams[‘font.family‘]=[‘SimHei‘] 
plt.rcParams[‘axes.unicode_minus‘]=False 
labels=‘青蛙‘,‘猪‘,‘狗子‘,‘原木‘
sizes=25,20,45,60
colors=‘yellowgreen‘,‘gold‘,‘lightskyblue‘,‘lightcoral‘
explode=0,0.2,0,0
plt.pie(sizes,explode=explode,labels=labels,colors=colors,autopct=‘%1.2f%%‘,shadow=True,startangle=50)
plt.axis(‘equal‘)
plt.show()

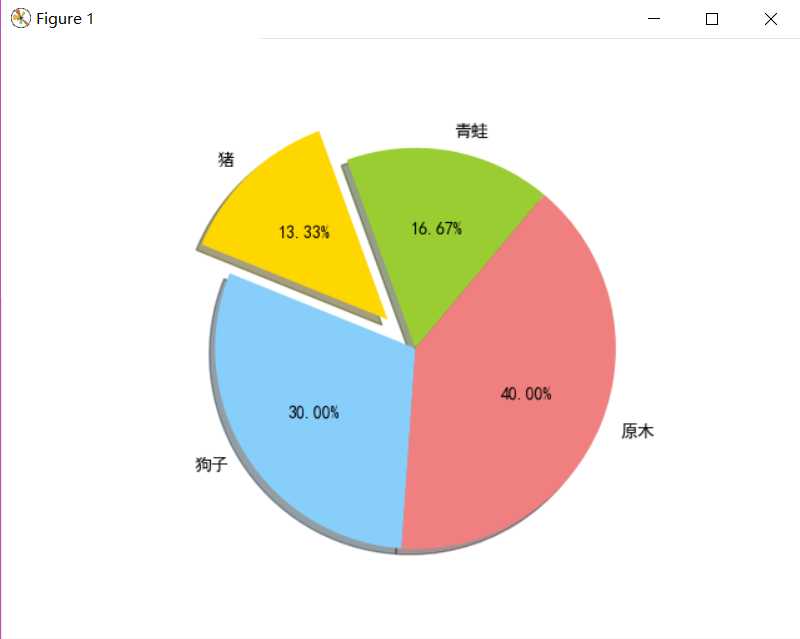
ok~

当制作折线图的时候，我们还会运用其他一些功能：

线条标记及相关属性：

线条风格linestyle或ls	描述
‘-‘	实线
‘—‘	破折线
‘-.‘	点划线
‘:‘	虚线
‘None‘,‘‘,‘‘	什么都不画

 

 

 

 

 

 

 

标记masker	描述	标记	描述
‘o‘	圆圈	‘.’	点
‘D‘	菱形	‘s‘	正方形
‘h‘	六边形1	‘*‘	星号
‘H‘	六边形2	‘d‘	小菱形
‘_‘	水平线	‘v‘	一角朝下的三角形
‘8‘	八边形	‘<‘	一角朝左的三角形
‘p‘	五边形	‘>‘	一角朝右的三角形
‘,‘	像素	‘^‘	一角朝上的三角形
‘+‘	加号	‘	‘
‘None‘,‘‘,‘‘	无	‘x‘	X

 

 

 

 

 

 

 

 

 

 

当然还有颜色，背景颜色等参数的设置，具体跟其他常规库别无二致。

例如：

通过向如matplotlib.pyplot.axes()或者matplotlib.pyplot.subplot()这样的方法提供一个axisbg参数，可以指定坐标这的背景色。

subplot(111,axisbg=(0.1843,0.3098,0.3098)

通过更深入的学习，折线图，条形图，饼图，流程图，梯形图等等你都能制作，结合numpy的数据分析，你能够运用强大的计算分析众多数据，让你更直观地认识，理解眼前的世界！

（形式丰富的分析图形表格）

 下面是我的实例！！

成绩雷达图：

import matplotlib.pyplot as plt
import numpy as np
import matplotlib
plt.rcParams[‘font.family‘]=‘SimHei‘

labels=np.array([‘总成绩‘,‘单选‘,‘程序题‘,‘剩余用时‘,‘复写率‘])
nAttr=5
data=np.array([7.4,8,6.8,2,9])
angles=np.linspace(0,2*np.pi,nAttr,endpoint=False)
data=np.concatenate((data,[data[0]]))
angles=np.concatenate((angles,[angles[0]]))
fig=plt.figure(facecolor=‘white‘)
plt.subplot(111,polar=True)
plt.plot(angles,data,‘b*-‘,color=‘y‘,linewidth=3)
plt.fill(angles,data,facecolor=‘g‘,alpha=0.25)
plt.thetagrids(angles*180/np.pi,labels)
plt.figtext(0.52,0.95,‘iconangle的成绩表‘,ha=‘center‘)
plt.grid(True)
plt.savefig(‘scorce_radar.JPG‘)
plt.show()

效果：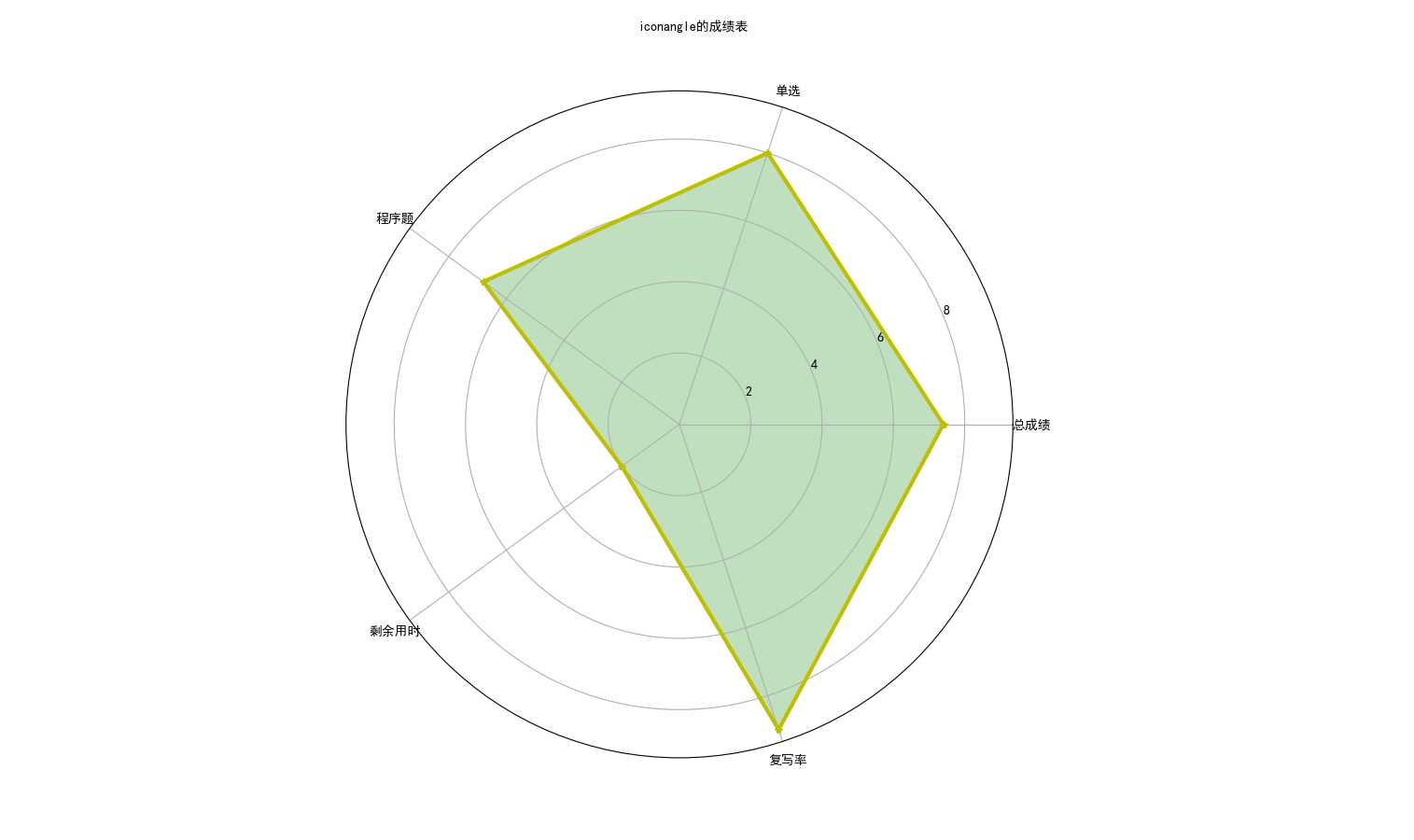

看上去我的单选似乎更强一点（耸肩）

进阶地，研究一个物理规律：我选择研究单摆

伽利略曾对单摆的运动产生浓厚的兴趣，我通过查找单摆的运动公式，得到一个这样的单摆周期计算公式：

T=2π√(L/g)

 那么利用numpy以及matplotlib可以绘制出这个规律的模型：

代码如下：

import matplotlib.pyplot as plt
import numpy as np

plt.rcParams[‘font.family‘]=‘SimHei‘
plt.title("在重力加速度为9.8m/s的时候单摆的周期（T）与摆长（L）关系")
plt.xlabel(‘摆长（L）‘)
plt.ylabel(‘周期（T）‘)
x=np.linspace(0.0,40.0,1000)
y=2*np.pi*np.sqrt(x/9.8)
plt.plot(x,y,‘k‘,color=‘g‘,linewidth=3,linestyle=‘-‘)
plt.show()

效果：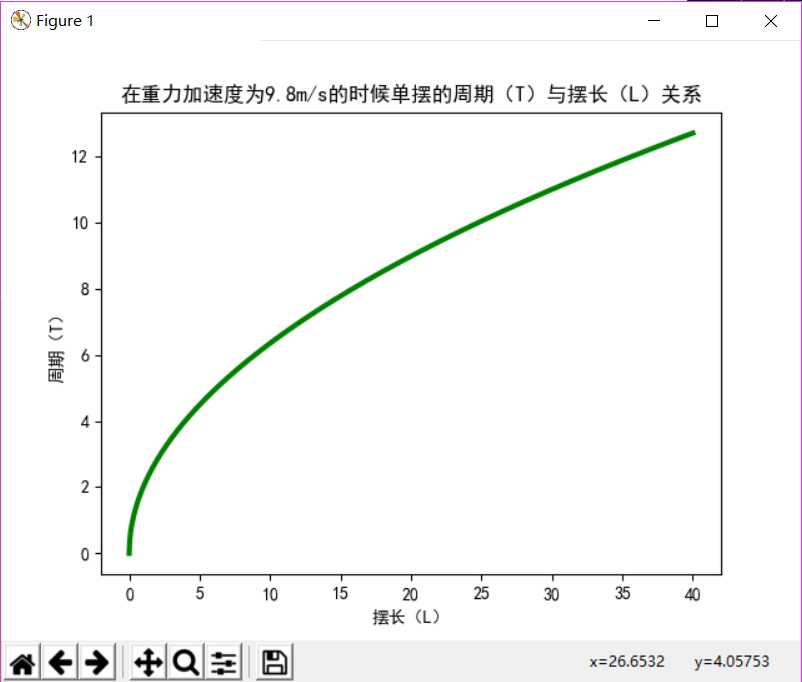

直观又美观！相当棒！

那么今天的学习分享就先到这里啦~谢谢关注！！