PTA Root of AVL Tree （AVL树模板+四种旋转+指针）

Posted 2021-02-17 chenyangxu

 

 

 

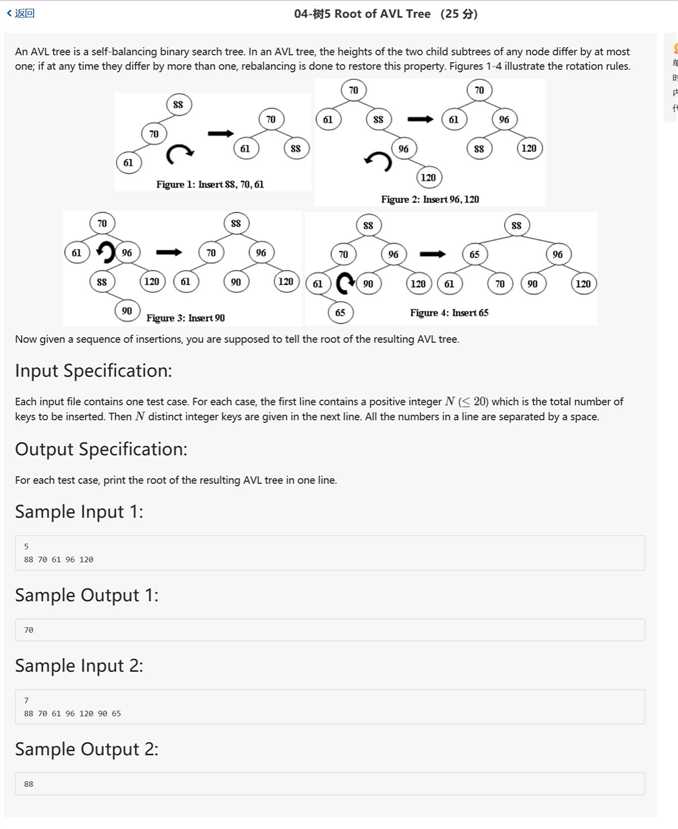
关于AVL树（平衡二叉搜索树，高度为lgn）的讲解，双手呈上某大佬博客：https://www.cnblogs.com/zhuwbox/p/3636783.html

我从这题get到一个新的结构体写法（姿势）：

typedef struct treeNode
{
    int val;
    treeNode *left;
    treeNode *right;
    int height;
}node, *tree;//node 是treeNode结构体，*tree是结构体指针

 

我对AVL树的理解：

按照插入节点时旋转的次数划分，可以分为两种旋转（单旋和双旋）；继续划分，按照插入节点在根节点左右子树的不同，可以具体划分为四种旋转：单旋转：单左右旋（左左右旋），单右左旋（右右左旋）；双旋转：左右左右旋，右左右左旋

例子（搬运于大佬博客）：

 

 

 

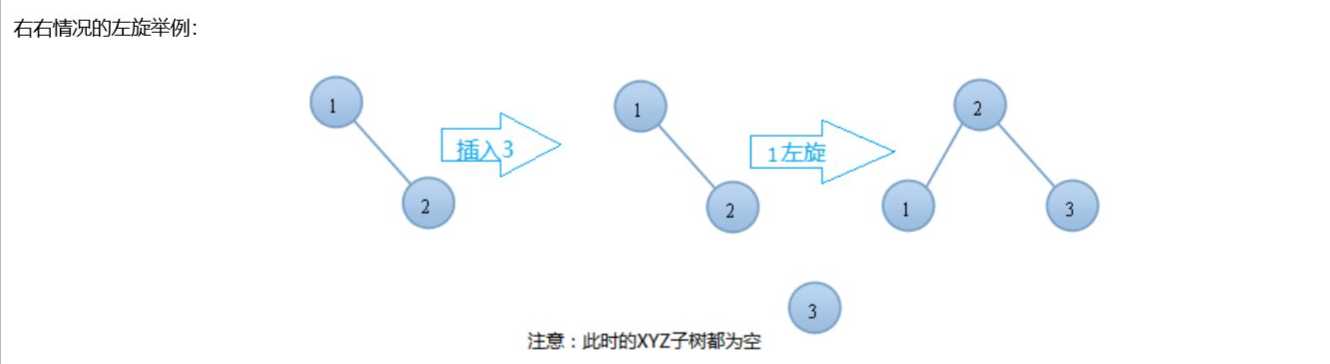
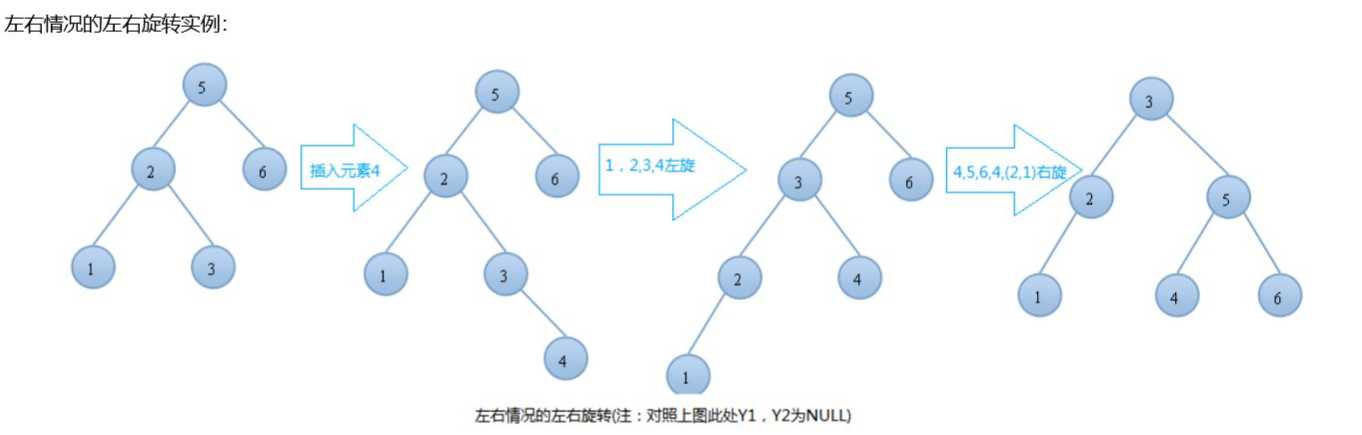
代码：

 

tree rightRotation(tree t)//左左右旋
{
    tree l=t->left;
    t->left=l->right;
    l->right=t;
    t->height=max(height(t->left), height(t->right))+1;//跟新节点高度
    l->height=max(height(l->left), height(l->right))+1;
    return l;//l是新的根
}

tree leftRotation(tree t)//右右左旋
{
    tree l=t->right;
    t->right=l->left;
    l->left=t;
    t->height=max(height(t->left), height(t->right))+1;//跟新节点高度
    l->height=max(height(l->left), height(l->right))+1;
    return l;//l是新的根
}

tree leftRightRotation(tree t)//左右左右旋
{
    t->left=leftRotation(t->left);
    return rightRotation(t);
}

tree rightLeftRotation(tree t)//右左右左旋
{
    t->right=rightRotation(t->right);
    return leftRotation(t);
}

建树函数很简单，插入节点函数要特别提一下。如果t为NULL（树还没有根），那么初始化根节点；如果t非空且val>t->val，插入右节点；如果t非空且val<t->val，插入左节点。一旦高度差值为2，进行相应的AVL旋转（先插入节点再旋转），最后跟新t节点高度。代码：

tree treeCreate(tree t)
{
    int val;
    for(int i=1;i<=n;++i){
        cin>>val;
        t=nodeInsert(t, val);
    }
    return t;
}

tree nodeInsert(tree t, int val)
{
    if(!t) {t=new node;t->left=t->right=NULL;t->height=0;t->val=val;}
    else if(val>t->val) {//向节点右边插入值
        t->right=nodeInsert(t->right, val);//先插入后旋转
        if(height(t->right)-height(t->left)==2) {//只会出现右节点比左节点大2的情况
            if(val>t->right->val)
                t=leftRotation(t);//右右左旋
           else
                t=rightLeftRotation(t);//右左右左旋
        }
    }
    else if(val<t->val) {//向节点左边插入
        t->left=nodeInsert(t->left, val);
        if(height(t->left)-height(t->right)==2) {
            if(val<t->left->val)
                t=rightRotation(t);//左左右旋
            else
                t=leftRightRotation(t);//左右左右旋
        }
    }
    t->height=max(height(t->left), height(t->right))+1;//更新height
    return t;
}

main函数中定义树根t，注意将t设置为NULL，否则t作为野指针难以维护（我不会告诉你这是我调了靠近一个小时的bug）

{
    cin>>n;
    tree t=NULL;//先指定t指向NULL，否则t是野指针，非常难处理
    t=treeCreate(t);
    if(t) cout<<t->val<<endl;
    return 0;
}

全部代码：

#include <bits/stdc++.h>
using namespace std;
//AVL树的四种旋转情况：单旋转：左左右旋，右右左旋，左右左右旋，右左右左旋

int n;
typedef struct treeNode
{
    int val;
    treeNode *left;
    treeNode *right;
    int height;
}node, *tree;//node 是treeNode结构体，*tree是结构体指针

int height(tree t)//计算树的高度
{
    if(!t) return 0;//空树
    return t->height;
}

tree rightRotation(tree t)//左左右旋
{
    tree l=t->left;
    t->left=l->right;
    l->right=t;
    t->height=max(height(t->left), height(t->right))+1;//跟新节点高度
    l->height=max(height(l->left), height(l->right))+1;
    return l;//l是新的根
}

tree leftRotation(tree t)//右右左旋
{
    tree l=t->right;
    t->right=l->left;
    l->left=t;
    t->height=max(height(t->left), height(t->right))+1;//跟新节点高度
    l->height=max(height(l->left), height(l->right))+1;
    return l;//l是新的根
}

tree leftRightRotation(tree t)//左右左右旋
{
    t->left=leftRotation(t->left);
    return rightRotation(t);
}

tree rightLeftRotation(tree t)//右左右左旋
{
    t->right=rightRotation(t->right);
    return leftRotation(t);
}

tree nodeInsert(tree t, int val)
{
    if(!t) {t=new node;t->left=t->right=NULL;t->height=0;t->val=val;}
    else if(val>t->val) {//向节点右边插入值
        t->right=nodeInsert(t->right, val);//先插入后旋转
        if(height(t->right)-height(t->left)==2) {//只会出现右节点比左节点大2的情况
            if(val>t->right->val)
                t=leftRotation(t);//右右左旋
           else
                t=rightLeftRotation(t);//右左右左旋
        }
    }
    else if(val<t->val) {//向节点左边插入
        t->left=nodeInsert(t->left, val);
        if(height(t->left)-height(t->right)==2) {
            if(val<t->left->val)
                t=rightRotation(t);//左左右旋
            else
                t=leftRightRotation(t);//左右左右旋
        }
    }
    t->height=max(height(t->left), height(t->right))+1;//更新height
    return t;
}

tree treeCreate(tree t)
{
    int val;
    for(int i=1;i<=n;++i){
        cin>>val;
        t=nodeInsert(t, val);
    }
    return t;
}

void lrd(tree t)//后序遍历 输出调试
{
    if(t){
        lrd(t->left);
        lrd(t->right);
        cout<<t->val<<endl;
    }
}
int main()
{
    cin>>n;
    tree t=NULL;//先指定t指向NULL，否则t是野指针，非常难处理
    t=treeCreate(t);
    //lrd(t);
    if(t) cout<<t->val<<endl;
    return 0;
}