博弈题目小结

Posted 2021-02-17 ymzjj

 

HDU 2174 kiki‘s game

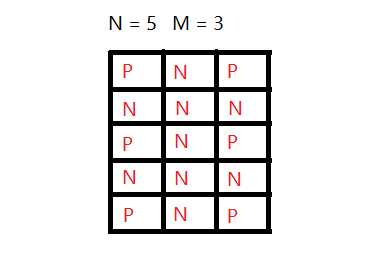
题意：有一个N*M的棋盘，起点在右上角，两个人每轮可把棋子向左、向下或者向左下移动一格，直到不能移动棋子者输。

NP图解决：

概念：

必败点（P点）：前一个选手将取胜的位置称为必败点。

必胜点（N点）：下一个选手将取胜的位置成为必胜点。

 

性质：

 

步骤：

 

 NP图：

 

AC code:

 1 #include <bits/stdc++.h>
 2 #define inc(i, j, k) for(int i = j; i <= k; i++)
 3 #define rep(i, j, k) for(int i = j; i < k; i++)
 4 #define F(x) ((x)/3+((x)%3==1?0:tb))
 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)
 6 #define INF 0x3f3f3f3f
 7 #define LL long long
 8 #define MEM(i, j) memset(i, j, sizeof(i));
 9 #define gcd(i, j) __gcd(i, j)
10 using namespace std;
11 
12 int main()
13 {
14     int a, b;
15     while(~scanf("%d %d", &a, &b)){
16         if(a == 0 && b == 0) break;
17         if(a%2 == 1 && b%2 == 1) puts("What a pity!");
18         else puts("Wonderful!");
19     }
20     return 0;
21 }

View Code

 

 

 HDU 2149  Public Sale

题意：

底价为 0，最低成交价为 M，两位博弈，每轮叫价区间 1~N

求 先手开始有多少种取胜叫价，输出每种叫价值。

 

解题思路：

巴什博弈变形，只要能把 （N+1) * t 留给对手必胜，如果自己是(N+1)*r 必败。

AC code:

 1 #include <bits/stdc++.h>
 2 #define inc(i, j, k) for(int i = j; i <= k; i++)
 3 #define rep(i, j, k) for(int i = j; i < k; i++)
 4 #define F(x) ((x)/3+((x)%3==1?0:tb))
 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)
 6 #define INF 0x3f3f3f3f
 7 #define LL long long
 8 #define MEM(i, j) memset(i, j, sizeof(i));
 9 #define gcd(i, j) __gcd(i, j)
10 using namespace std;
11 
12 int main()
13 {
14     int N, M;
15     while(~scanf("%d %d", &M, &N)){
16         if(M <= N){
17             for(int i = M; i <= N; i++){
18                 printf("%d%c", i, i==N?‘
‘:‘ ‘);
19             }
20         }
21         else if(M%(N+1) == 0) puts("none");
22         else{
23             printf("%d
", M%(N+1));
24         }
25     }
26     return 0;
27 }

View Code

 

HDU 1907 John

题意：

有 N 堆物品，每轮选着一堆拿走若干物品，拿走最后一个物品的输；

解题思路：

Nim博弈变形，异或判断是否为奇异局势， 面对奇异局势先手必败，如果全是 1 判断奇偶性，偶数则先手胜。

AC code：

 1 #include <bits/stdc++.h>
 2 #define inc(i, j, k) for(int i = j; i <= k; i++)
 3 #define rep(i, j, k) for(int i = j; i < k; i++)
 4 #define F(x) ((x)/3+((x)%3==1?0:tb))
 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)
 6 #define INF 0x3f3f3f3f
 7 #define LL long long
 8 #define MEM(i, j) memset(i, j, sizeof(i));
 9 #define gcd(i, j) __gcd(i, j)
10 using namespace std;
11 char ans1[] = "John", ans2[] = "Brother";
12 int main()
13 {
14     int N, sum;
15     bool flag = false;
16     int T_case, tp;
17     scanf("%d", &T_case);
18     while(T_case--){
19         flag = false;
20         scanf("%d", &N);scanf("%d", &sum);
21         if(sum > 1) flag = true;
22         inc(i, 2, N){
23             scanf("%d", &tp);
24             if(tp > 1) flag = true;
25             sum^=tp;
26         }
27         if(!flag) printf("%s", N%2?ans2:ans1);
28         else printf("%s", sum==0?ans2:ans1);
29         puts("");
30     }
31     return 0;
32 }

View Code

 

 

HDU 2509 Be the Winner

题意：同上；

解题思路：同上；

 

HDU 1850 Being a Good Boy in Spring Festival

题意：有 N 堆 扑克牌，每轮选择其中一堆拿走任意张牌，拿走最后一张牌的胜，问先手如果想取胜，第一步有多少种选择？

解题思路：

Nim博弈变形；

原理、方法都很详细：https://www.cnblogs.com/kuangbin/archive/2011/11/24/2262389.html

即枚举每一堆是否可以删掉一些值变成奇异局势。

AC code:

 1 #include <bits/stdc++.h>
 2 #define inc(i, j, k) for(int i = j; i <= k; i++)
 3 #define rep(i, j, k) for(int i = j; i < k; i++)
 4 #define F(x) ((x)/3+((x)%3==1?0:tb))
 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)
 6 #define INF 0x3f3f3f3f
 7 #define LL long long
 8 #define MEM(i, j) memset(i, j, sizeof(i));
 9 #define gcd(i, j) __gcd(i, j)
10 using namespace std;
11 const int MAXN = 2e5+10;
12 int tp[MAXN];
13 int main()
14 {
15     int N, sum = 0;
16     while(~scanf("%d", &N) && N){
17         int ans = 0;
18         scanf("%d", &sum);
19         tp[1] = sum;
20         inc(i, 2, N){
21             scanf("%d", &tp[i]);
22             sum^=tp[i];
23         }
24         inc(i, 1, N){
25             if(tp[i] > (sum^tp[i])) ans++;
26         }
27         printf("%d
", ans);
28     }
29     return 0;
30 }

View Code

 

 

HDU 1536 S-Nim

题意：

给出一个集合 S 表示游戏中可选的数目，接下来给定 M 个游戏局面即 N 堆物品的大小。两人轮流选择一堆取数 只能取 ∈S 的数目，取走最后一个胜。判断游戏局面是先手胜还是后手胜。

题目给出了SG函数的用途和求法。

解题思路：

SG函数模板。

AC code:

 1 #include <bits/stdc++.h>
 2 #define inc(i, j, k) for(int i = j; i <= k; i++)
 3 #define rep(i, j, k) for(int i = j; i < k; i++)
 4 #define F(x) ((x)/3+((x)%3==1?0:tb))
 5 #define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)
 6 #define INF 0x3f3f3f3f
 7 #define LL long long
 8 #define MEM(i, j) memset(i, j, sizeof(i));
 9 #define gcd(i, j) __gcd(i, j)
10 using namespace std;
11 const int MAXN = 2e3+10;
12 const int MM = 1e4+5;
13 int S[MAXN], sg[MM];
14 int vis[MM];
15 string ans;
16 
17 void getsg(int n)
18 {
19     sg[0] = 0;
20     memset(vis, -1, sizeof(vis));
21     inc(i, 1, MM){
22         inc(j, 1, n){
23             if(S[j] > i) break;
24             vis[sg[i-S[j]]] = i;
25         }
26 //        puts("zjj");
27         int k = 0;
28         while(vis[k] == i) k++;
29         sg[i] = k;
30     }
31 }
32 
33 int main()
34 {
35     int N, M, K, tp, res;
36 
37     while(~scanf("%d", &N) && N){
38         ans = "";
39         inc(i, 1, N) scanf("%d", &S[i]);
40         //inc(i, 1, N) printf("%d ", S[i]);
41         sort(S+1, S+N+1);
42         getsg(N);
43 //        puts("zjj");
44         scanf("%d", &K);
45         while(K--){
46             scanf("%d", &M);
47 //            scanf("%d", &res);
48             res = 0;
49             inc(i, 1, M){
50                 scanf("%d", &tp);
51                 res^=sg[tp];
52             }
53             if(res == 0) ans+=‘L‘;
54             else ans+=‘W‘;
55         }
56         cout << ans << endl;
57     }
58 
59     return 0;
60 }

View Code