二叉树遍历必知方式
Posted ivoo
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了二叉树遍历必知方式相关的知识,希望对你有一定的参考价值。
概述:本文主要讲述二叉树的前序、中序、后序遍历的递归与非递归实现及广度优先遍历、深度优先遍历和之字形遍历。
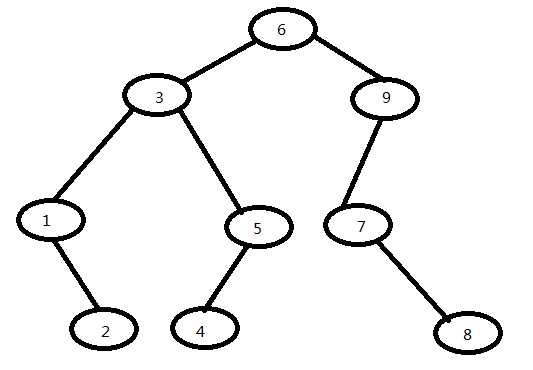
正确的输出结果是:

(1)先序遍历 以根左右的顺序进行遍历
- 递归方式
//<editor-fold desc="先序遍历-递归"> private void preOrderTraversal(TreeNode root) { if (root == null) return; printNode(root); preOrderTraversal(root.left); preOrderTraversal(root.right); } // </editor-fold>
- 非递归方式
//<editor-fold desc="先序遍历-非递归"> private void preOrderTraversal_stack(TreeNode root) { if (root == null) return; TreeNode node = root; Stack<TreeNode> stack = new Stack<>(); while (node != null || !stack.isEmpty()) { if (node != null) { printNode(node); stack.push(node); node = node.left; } else { node = stack.pop(); node = node.right; } } } // </editor-fold>
(2)中序遍历 以左根右的顺序进行遍历
- 递归方式
//<editor-fold desc="中序遍历-递归"> private void inOrderTraversal(TreeNode root) { if (root == null) return; inOrderTraversal(root.left); printNode(root); inOrderTraversal(root.right); } // </editor-fold>
- 非递归方式
//<editor-fold desc="中序遍历-非递归"> private void inOrderTraversal_stack(TreeNode root) { if (root == null) return; TreeNode node = root; Stack<TreeNode> stack = new Stack<>(); while (node != null || !stack.isEmpty()) { if (node != null) { stack.push(node); node = node.left; } else { node = stack.pop(); printNode(node); node = node.right; } } } // </editor-fold>
(3)后序遍历 以左右根的顺序进行遍历
- 递归方式
//<editor-fold desc="后序遍历-递归"> private void postOrderTraversal(TreeNode root) { if (root == null) return; postOrderTraversal(root.left); postOrderTraversal(root.right); printNode(root); } // </editor-fold>
- 非递归方式
//<editor-fold desc="后序遍历-非递归"> private void postOrderTraversal_stack(TreeNode root) { if (root == null) return; TreeNode node = root; Stack<TreeNode> stack = new Stack<>(); Stack<TreeNode> outStack = new Stack<>(); while (node != null || !stack.isEmpty()) { if (node != null) { stack.push(node); outStack.push(node); node = node.right; } else { node = stack.pop(); node = node.left; } } while (!outStack.isEmpty()) { printNode(outStack.pop()); } } // </editor-fold>
(4)广度优先遍历
//<editor-fold desc="广度优先遍历"> private void breadthFirstTraversal(TreeNode root) { if (root == null) return; ArrayDeque<TreeNode> deque = new ArrayDeque<>(); deque.add(root); while (!deque.isEmpty()) { TreeNode node = deque.remove(); printNode(node); if (node.left != null) { deque.add(node.left); } if (node.right != null) { deque.add(node.right); } } } // </editor-fold>
(5)深度优先遍历
//<editor-fold desc="深度优先遍历"> private void depthFirstTraversal(TreeNode root) { if (root == null) return; Stack<TreeNode> stack = new Stack<>(); stack.push(root); while (!stack.isEmpty()) { TreeNode node = stack.pop(); printNode(node); if (node.right != null) { stack.push(node.right); } if (node.left != null) { stack.push(node.left); } } } // </editor-fold>
(6)之字形遍历
//<editor-fold desc="之字形遍历"> private void zhiTraversal(TreeNode root) { if (root == null) return; Stack<TreeNode> stack1 = new Stack<>(); Stack<TreeNode> stack2 = new Stack<>(); stack1.push(root); int grade = 1; while (!stack1.isEmpty() || !stack2.isEmpty()) { if (grade % 2 == 1) { while (!stack1.isEmpty()) { TreeNode node = stack1.pop(); printNode(node); if (node.right != null) stack2.push(node.right); if (node.left != null) stack2.push(node.left); } } else if (grade % 2 == 0) {//偶数行 while (!stack2.isEmpty()) { TreeNode node = stack2.pop(); printNode(node); if (node.left != null) stack1.push(node.left); if (node.right != null) stack1.push(node.right); } } grade++; } } // </editor-fold>
完整代码如下

public class TreeTraversal { public static void main(String[] args) { TreeTraversal traversal = new TreeTraversal(); TreeNode root = traversal.initTree(); System.out.println("先序遍历"); traversal.preOrderTraversal(root); System.out.println(" 中序遍历"); traversal.inOrderTraversal(root); System.out.println(" 后序遍历"); traversal.postOrderTraversal(root); System.out.println(" ================================ 先序遍历"); traversal.preOrderTraversal_stack(root); System.out.println(" 中序遍历"); traversal.inOrderTraversal_stack(root); System.out.println(" 后序遍历"); traversal.postOrderTraversal_stack(root); System.out.println(" ================================ 广度优先遍历"); traversal.breadthFirstTraversal(root); System.out.println(" 深度优先遍历"); traversal.depthFirstTraversal(root); System.out.println(" 之字形遍历"); traversal.zhiTraversal(root); } private TreeNode initTree() { TreeNode J = new TreeNode(8, null, null); TreeNode H = new TreeNode(4, null, null); TreeNode G = new TreeNode(2, null, null); TreeNode F = new TreeNode(7, null, J); TreeNode E = new TreeNode(5, H, null); TreeNode D = new TreeNode(1, null, G); TreeNode C = new TreeNode(9, F, null); TreeNode B = new TreeNode(3, D, E); TreeNode A = new TreeNode(6, B, C); return A; //返回根节点 } private void printNode(TreeNode node) { System.out.print(node.val + " "); } //<editor-fold desc="先序遍历-递归"> private void preOrderTraversal(TreeNode root) { if (root == null) return; printNode(root); preOrderTraversal(root.left); preOrderTraversal(root.right); } // </editor-fold> //<editor-fold desc="中序遍历-递归"> private void inOrderTraversal(TreeNode root) { if (root == null) return; inOrderTraversal(root.left); printNode(root); inOrderTraversal(root.right); } // </editor-fold> //<editor-fold desc="后序遍历-递归"> private void postOrderTraversal(TreeNode root) { if (root == null) return; postOrderTraversal(root.left); postOrderTraversal(root.right); printNode(root); } // </editor-fold> //<editor-fold desc="先序遍历-非递归"> private void preOrderTraversal_stack(TreeNode root) { if (root == null) return; TreeNode node = root; Stack<TreeNode> stack = new Stack<>(); while (node != null || !stack.isEmpty()) { if (node != null) { printNode(node); stack.push(node); node = node.left; } else { node = stack.pop(); node = node.right; } } } // </editor-fold> //<editor-fold desc="中序遍历-非递归"> private void inOrderTraversal_stack(TreeNode root) { if (root == null) return; TreeNode node = root; Stack<TreeNode> stack = new Stack<>(); while (node != null || !stack.isEmpty()) { if (node != null) { stack.push(node); node = node.left; } else { node = stack.pop(); printNode(node); node = node.right; } } } // </editor-fold> //<editor-fold desc="后序遍历-非递归"> private void postOrderTraversal_stack(TreeNode root) { if (root == null) return; TreeNode node = root; Stack<TreeNode> stack = new Stack<>(); Stack<TreeNode> outStack = new Stack<>(); while (node != null || !stack.isEmpty()) { if (node != null) { stack.push(node); outStack.push(node); node = node.right; } else { node = stack.pop(); node = node.left; } } while (!outStack.isEmpty()) { printNode(outStack.pop()); } } // </editor-fold> //<editor-fold desc="广度优先遍历"> private void breadthFirstTraversal(TreeNode root) { if (root == null) return; ArrayDeque<TreeNode> deque = new ArrayDeque<>(); deque.add(root); while (!deque.isEmpty()) { TreeNode node = deque.remove(); printNode(node); if (node.left != null) { deque.add(node.left); } if (node.right != null) { deque.add(node.right); } } } // </editor-fold> //<editor-fold desc="深度优先遍历"> private void depthFirstTraversal(TreeNode root) { if (root == null) return; Stack<TreeNode> stack = new Stack<>(); stack.push(root); while (!stack.isEmpty()) { TreeNode node = stack.pop(); printNode(node); if (node.right != null) { stack.push(node.right); } if (node.left != null) { stack.push(node.left); } } } // </editor-fold> //<editor-fold desc="之字形遍历"> private void zhiTraversal(TreeNode root) { if (root == null) return; Stack<TreeNode> stack1 = new Stack<>(); Stack<TreeNode> stack2 = new Stack<>(); stack1.push(root); int grade = 1; while (!stack1.isEmpty() || !stack2.isEmpty()) { if (grade % 2 == 1) { while (!stack1.isEmpty()) { TreeNode node = stack1.pop(); printNode(node); if (node.right != null) stack2.push(node.right); if (node.left != null) stack2.push(node.left); } } else if (grade % 2 == 0) {//偶数行 while (!stack2.isEmpty()) { TreeNode node = stack2.pop(); printNode(node); if (node.left != null) stack1.push(node.left); if (node.right != null) stack1.push(node.right); } } grade++; } } // </editor-fold> }
二叉树定义如下

public class TreeNode { public int val = 0; public TreeNode left = null; public TreeNode right = null; public TreeNode(int val) { this.val = val; } public TreeNode(int val, TreeNode left, TreeNode right) { this.val = val; this.left = left; this.right = right; } }
以上是关于二叉树遍历必知方式的主要内容,如果未能解决你的问题,请参考以下文章
