POJ1179Polygon(区间dp)
Posted xishirujin
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了POJ1179Polygon(区间dp)相关的知识,希望对你有一定的参考价值。
啊~~
被dp摁在地上摩擦的人
今天做了一道区间dp的题(POJ1179Polygon)
题目:
Polygon
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 6951 | Accepted: 2975 |
Description
Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N.
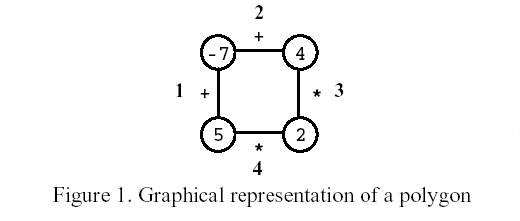
On the first move, one of the edges is removed. Subsequent moves involve the following steps:
?pick an edge E and the two vertices V1 and V2 that are linked by E; and
?replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.
Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.
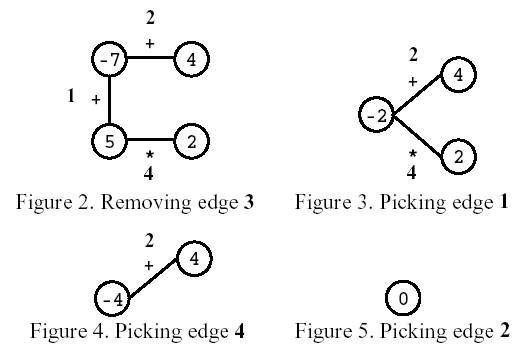
Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.

On the first move, one of the edges is removed. Subsequent moves involve the following steps:
?pick an edge E and the two vertices V1 and V2 that are linked by E; and
?replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.
Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.

Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.
Input
Your
program is to read from standard input. The input describes a polygon
with N vertices. It contains two lines. On the first line is the number
N. The second line contains the labels of edges 1, ..., N, interleaved
with the vertices‘ labels (first that of the vertex between edges 1 and
2, then that of the vertex between edges 2 and 3, and so on, until that
of the vertex between edges N and 1), all separated by one space. An
edge label is either the letter t (representing +) or the letter x
(representing *).
3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].
3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].
Output
Your
program is to write to standard output. On the first line your program
must write the highest score one can get for the input polygon. On the
second line it must write the list of all edges that, if removed on the
first move, can lead to a game with that score. Edges must be written in
increasing order, separated by one space.
Sample Input
4 t -7 t 4 x 2 x 5
Sample Output
33 1 2
题目翻译:
被某种生物吃掉了~~懒
自行翻译╮( ̄▽ ̄)╭
好了,我们现在来看这道题,刚开始拿到这道题时,我看的十分懵逼,恕我直言,我是看了题解的= =b
首先,我们先弄懂题意,让我们首先去拿去一条边,是这个环换为一条链,所以,这个时候我们就有一步操作,来将环变为链。每一回把值赋到当前点和加n的点上。
然后,我们看到操作是将两个数合为一个,和石子合并很相像,所以我们就可以沿用石子合并的思路,区间动态规划。
这时我们就来考虑数值转移时的最大最小值,我们很容易想到用两个数组来进行维护最大最小值。而且在转移时的最大值和最小值分为+和*两种不同结构
第一,当为+时,最大值就是两阶段最大值相加,最小值是两阶段最小值相加。
其次,我们来看*的情况,不难想到,我们可以想到最大值*最大值,但是我们可以知道最大最小值有负数,所以此时最大值就不唯一,比如说最小*最小,负*负=正!!
所以,我们就有多种情况进行讨论。
code:
1 f2[i][j]=max(f2[i][j],max(f1[i][k]*f1[k+1][j],f2[i][k]*f2[k+1][j])); 2 f1[i][j]=min(f1[i][j],min(f1[i][k]*f2[k+1][j],min(f2[i][k]*f1[k+1][j],f1[i][k]*f1[k+1][j])));//f1表示最大值,f2表示最小值
最关键的部分我们已经知道了,现在我们就来解决答案输出的问题,

其实我们要得到题目最大值同种最大值的多种情况
我们先来解决一下最大值的问题:
1 for(int i=1;i<=n;i++){ 2 ans=max(ans,f2[i][i+n-1]);//表示在所有的点缩完后的答案 3 }
这样我们就得到了最大值。
然后我们来处理多情况问题。即我们去判断这个断边情况的答案,如果相等则输出。(因为是顺序的扫描,所以输出一定是有序的)。
1 for(int i=1;i<=n;i++){ 2 if(f2[i][i+n-1]==ans){ 3 printf("%d ",i); 4 } 5 }
这样我们就结束了这道题(注意毒瘤读入):

1 //#include<bits/stdc++.h> 2 #include<iostream> 3 #include<cstdio> 4 #include<string> 5 #include<cmath> 6 using namespace std; 7 template<typename type_of_scan> 8 void scan(type_of_scan &x){ 9 type_of_scan f=1;x=0;char s=getchar(); 10 while(s<‘0‘||s>‘9‘){if(s==‘-‘)f=-1;s=getchar();} 11 while(s>=‘0‘&&s<=‘9‘){x=x*10+s-‘0‘;s=getchar();} 12 x*=f; 13 } 14 const int N=1007; 15 int n; 16 int f1[N][N],f2[N][N],a[N]; 17 char c[N]; 18 int main(){ 19 scan(n); 20 // scanf("%d ",&n); 21 for(int i=1;i<=n;i++){ 22 // scanf("%c %d",&c[i],&a[i]);getchar();//ioi读入 ,虽然我也不知道为什么 23 scanf("%c",&c[i]); 24 c[i+n]=c[i]; 25 scan(a[i]); 26 a[i+n]=a[i]; 27 }//拆成两倍的链 28 for(int i=1;i<=n*2;i++){ 29 for(int j=1;j<=n*2;j++){ 30 f1[i][j]=0x3f3f3f3f;//最小值 31 f2[i][j]=-0x3f3f3f3f;//最大值 32 if(i==j)f1[i][j]=f2[i][j]=a[i];//赋值点 33 } 34 } 35 for(int l=2;l<=n;l++){ 36 for(int i=1;i<=n*2-l+1;i++){ 37 int j=i+l-1; 38 for(int k=i;k<j;k++){ 39 if(c[k+1]==‘x‘){ 40 f2[i][j]=max(f2[i][j],max(f1[i][k]*f1[k+1][j],f2[i][k]*f2[k+1][j])); 41 f1[i][j]=min(f1[i][j],min(f1[i][k]*f2[k+1][j],min(f2[i][k]*f1[k+1][j],f1[i][k]*f1[k+1][j]))); 42 }else{ 43 f2[i][j]=max(f2[i][j],f2[i][k]+f2[k+1][j]); 44 f1[i][j]=min(f1[i][j],f1[i][k]+f1[k+1][j]); 45 } 46 } 47 } 48 } 49 int ans=0; 50 for(int i=1;i<=n;i++){ 51 ans=max(ans,f2[i][i+n-1]);//表示在所有的点缩完后的答案 52 } 53 printf("%d ",ans); 54 for(int i=1;i<=n;i++){ 55 if(f2[i][i+n-1]==ans){ 56 printf("%d ",i); 57 } 58 } 59 return 0; 60 }
结束。

以上是关于POJ1179Polygon(区间dp)的主要内容,如果未能解决你的问题,请参考以下文章
