树&堆

Posted 2021-02-16 naive-cat

树

什么是树？

大概像下面这样：

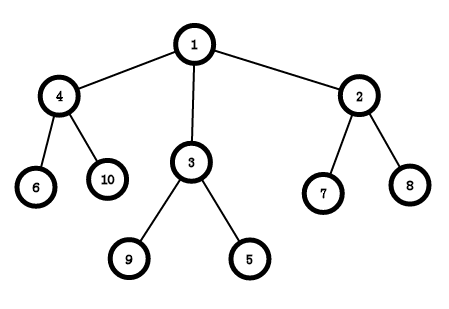
树的概念

树的每个点被称为节点；

连接的两个点，一个为父节点，一个为子节点，例如上图中，(1)是(4)的父节点，(4)是(1)的子节点；

没有父节点的节点称为根节点，注意：每一个非根节点的节点有且只有一个父节点；

没有子节点的节点称为叶子节点，如上图中，(6,10,5,9,7,8)是叶子节点；

一棵树必然由(n)个节点，(n-1)条边组成；

除了根节点外，每个子节点可以分为多个不相交的子树；

同“辈分”的节点在树的同一层里，例如上图，(2,3,4)是同一层的；

树的深度就是树的层数，例如上图，树的深度为(3)；

树里面没有环！

树的存储

使用结构体数组

struct node
{
    int data,father;
    //data代表这个节点的编号
    //father代表这个节点的父节点的编号
}tree[...];

二叉树

一种特殊的树，一个节点最多只能有(2)个子节点，大概长下面这样：

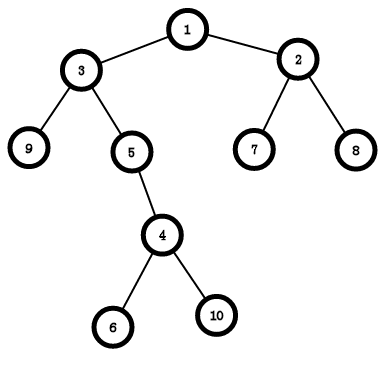
树的概念在二叉树中同样有用，另外，还有几个二叉树独有的性质：

在二叉树的第(i)层上最多有(2^{i-1})个节点((i ge 1))；

深度为(k)的二叉树至多有(2^{k-1})个节点((k ge 1))；

满二叉树

一棵深度为(n)，节点数为(2^{n-1})的二叉树，就像下图：

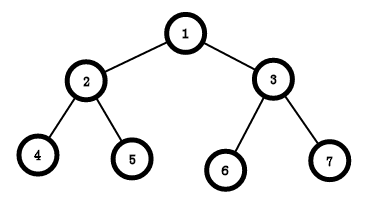
完全二叉树

一棵从上向下，从左向右标号和满二叉树对应的二叉树，如下图：

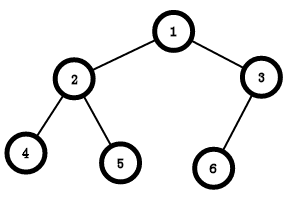
二叉树的存储

依然使用结构体数组。

struct node
{
    int lchild,rchild,father;
    //lchild代表这个节点的左子节点
    //rchild代表这个节点的右子节点
    //father代表这个节点的父节点的编号
}tree[...];

二叉树的遍历

前序遍历

二叉树的前序遍历顺序为：

1.访问父节点

2.前序遍历左子树

3.前序遍历右子树

(Code:)

void qianxu(int a)
{
    if(a)
    {
        cout<<a<<" ";
        qianxu(tree[a].lchild);
        qianxu(tree[a].rchild);
    }
    return ;
}

如上图，遍历结果为：1 3 9 5 4 6 10 2 7 8

中序遍历

二叉树的前序遍历顺序为：

1.前序遍历左子树

2.访问父节点

3.前序遍历右子树

(Code:)

void zhongxu(int a)
{
    if(a)
    {
        zhongxu(tree[a].lchild);
        cout<<a<<" ";
        zhongxu(tree[a].rchild);
    }
}

如上图，遍历结果为：9 3 6 4 10 5 1 7 2 8

后序遍历

二叉树的前序遍历顺序为：

1.前序遍历左子树

2.前序遍历右子树

3.访问父节点

(Code:)

void houxu(int a)
{
    if(a)
    {
        houxu(tree[a].lchild);
        houxu(tree[a].rchild);
        cout<<a<<" ";
    }
}

如上图，遍历结果为：9 6 10 4 5 3 7 8 2 1

堆

一种特殊的完全二叉树，分小根堆和大根堆两种堆。

大根堆：父节点一定比子节点大；

长的如下：

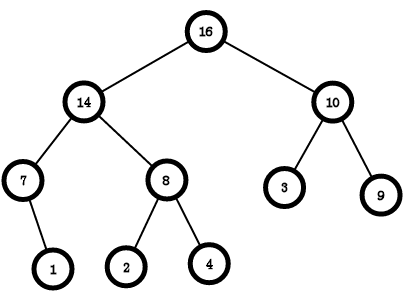
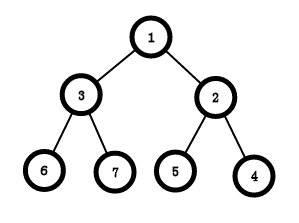
小根堆：父节点一定比子节点小。

长的如下：