自下而上建堆（heap）的时间复杂度证明

Posted 2021-02-16 zuotongbin

作者：Tobin
日期：2019/04/13
缘由：看python cookbook时，用到了heapq的库，书中提到，如果仅仅是返回一个数组的最大值，用max就可以了，但是如果返回多个较大或者较小元素用堆，如果返回的个数接近于数组本身的元素个数时，直接用排序即可。那么我在想，为啥返回几个元素的时候用堆效果比较好呢？于是我翻开了尘封许久的《算法导论》。

什么是堆

堆是一种数据结构。二叉堆是一个数组，近似于一个完全二叉树。树上的每个结点对应于数组的一个元素，除了最底层外树是充满的。下面的图是一个小根堆。即父节点的值要小于子结点，大根堆要相反。

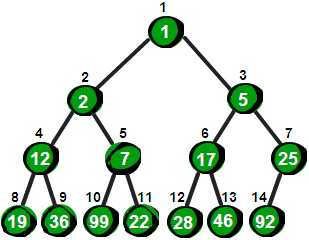
堆有哪些操作？复杂度如何证明。

建堆操作，调整操作，利用前两个进行的堆排序操作（建完堆后，不断将第一个元素与最后一个元素进行交换，然后调整，复杂度O（nlogn）。
主要是想记录下复杂度的证明，具体的堆如何操作就不细讲了，可以参考其它博客。
见图。

复杂度上界是O(2n)，在这之后，每次取一个最大元素并剔除后，进行调整的复杂度是O(logn)，也就是说在建完堆后，每次需要到最大值得复杂度是O（logn）。显然在返回多个较大元素的情况下，建堆进行操作的速度比遍历要快，遍历每次需要O(n)的时间。

堆有什么作用呢？

优先队列的底层是用堆来实现的。