二分图匹配

Posted 2021-02-16 bzmd

首先给定二分图定义

图中两个点集e1和e2

然后又一些无向边

u---v

其中u属于e1,v属于e2

匹配是指e1中一点u与e2中一点v相连则可以构成一个匹配

最大匹配是每个点仅属于一个匹配的情况下的最多匹配数

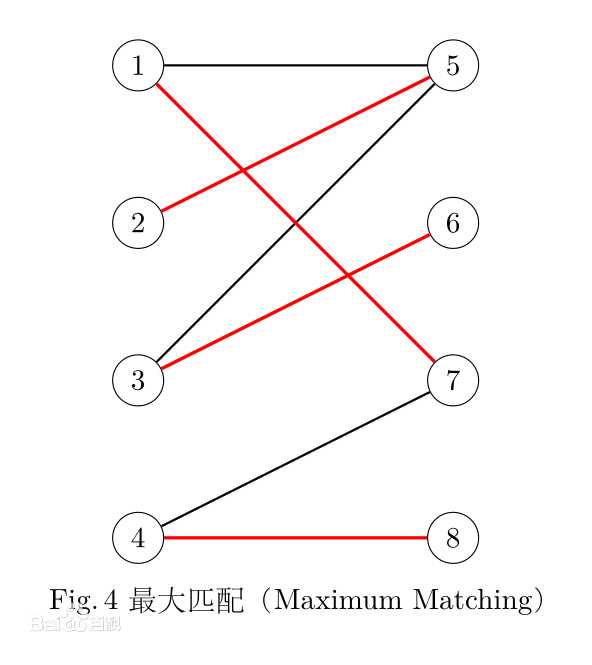
匹配边指的是已经用于匹配的边

增广路

经过一条非匹配边一条匹配边一条非匹配边一条匹配边.........一条非匹配边

然后把边的身份反转，就可以使总匹配数+1

例如图中假设一开始2-5,3-6 为非匹配边

3-5为匹配边

它们就可以构成一个增广路

 只要对于属于左边点集的每个点都做一次增广路，就能得到最大匹配

解释代码中的具体执行1...n属于点集1,n+1....n+m属于点集2

建边是建单向边，从点集1的点到点集2的点

pp[i]表示已经与点集二的点的已有匹配编号，如果尚无匹配则为0

vis[i]表示对点集1的点有没有加入这次的增广中

dfs返回值表示这次增广是否成功

之后对i=1...n每个点增广

先将vis清0

然后进入dfs，增广如果成功也要将pp[i]进行更改

洛谷3386

#include<cstdio>
#include<cstring>
const int N=2005;
struct E{
    int v,n;
}e[N*N];
int s,fir[N],pp[N],vis[N];
void add(int u,int v){
    e[++s].v=v;
    e[s].n=fir[u];
    fir[u]=s;
}
bool dfs(int u){
    for(int i=fir[u];i;i=e[i].n)
        if(!vis[e[i].v]){
            vis[e[i].v]=1;
            if(!pp[e[i].v]||dfs(pp[e[i].v])) return (pp[e[i].v]=u);
        }
    return 0;
}
int main(){
    int n,m,mm,u,v,ans=0;
    scanf("%d%d%d",&n,&m,&mm);
    while(mm--){
        scanf("%d%d",&u,&v);
        if(u<=n&&v<=m) add(u,v+n);
    }
    for(int i=1;i<=n;++i){
        memset(vis,0,sizeof(vis));
        if(dfs(i)) ++ans;
    }
    printf("%d",ans);
    return 0;
}