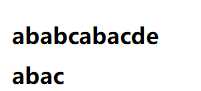（原创）数据结构之利用KMP算法解决串的模式匹配问题

Posted 2021-02-15 yewanting

 

 

 

给定一个主串S（长度<=10^6）和一个模式T（长度<=10^5），要求在主串S中找出与模式T相匹配的子串，返回相匹配的子串中的第一个字符在主串S中出现的位置。

输入格式:

输入有两行： 第一行是主串S； 第二行是模式T.

输出格式:

输出相匹配的子串中的第一个字符在主串S中出现的位置。若匹配失败，输出0.

输入样例:

在这里给出一组输入。例如：

aaaaaba
ba

输出样例:

在这里给出相应的输出。例如：

6


解题思路：串的模式匹配有两种：一种是BF算法，一种是KMP算法；
基于这道题给的数据，若用BF算法便会超时，所以我们这道题用KMP算法；
那么问题来了，KMP算法到底怎么用的；简单来讲，就是有两个步骤：
1、求模式串的next数组；
2、进行主串与模式串的匹配；
假设主串和模式串分别为

 

第一个问题：如何求next数组
??next数组求的是模式串的！！！
下面就以上面给的模式串为例；
next数组便是前缀中的最长相同前后缀，说起来比较绕，什么意思呢，模拟一遍就清楚了；


所以对于模式串对应的next数组为



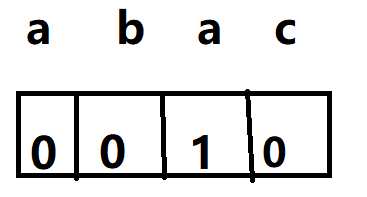
这样我们就求出了next数组；
接下来进行模式匹配，其实这样就会有个问题，所以实际上next数组这样是需要改进的；

 

假设我们不改进的话，进行匹配会出现什么问题呢；

进行模式匹配的大概代码如下：

1、即匹配，则i++;j++;

2、不匹配，根据刚刚求出的next数组，进行跳next数组；

下面代码中ssize为主串s的长度，tsize为模式串t的长度；

下面我们就根据代码模拟一遍；

 1     
 2                int i = 0 ;
 3                int j = 0;
 4         while(i<ssize&&j<tsize)
 5         {
 6             
 7                 if(s[i]==t[j])
 8             {
 9                 i++;
10                 j++;
11                 
12             }
13             else 
14             {
15                  j = next1[j];
16             }
17 
18             
19         }
20             
21             
22             if(j==tsize)
23             {
24                 cout <<  i-j+1;
25             }

上面我们求出来的next数组为：

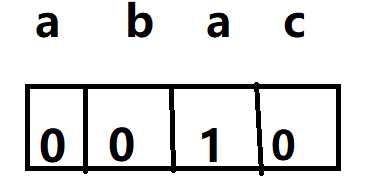
现在我们把它们的下面也写上：

 

 

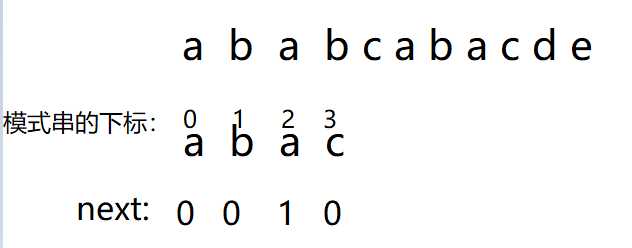
现在开始模拟一遍：

 

 

 

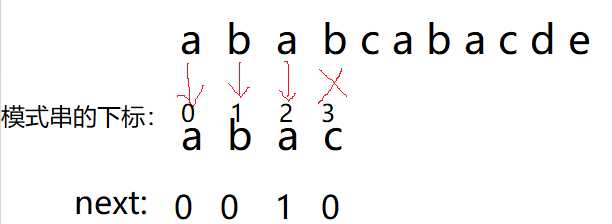
 我们发现匹配到c的时候不匹配了，跳next数组，则跳到下标为0处，变成：

 

 

 

 此时也不匹配，变成应该跳next数组，跳到下标为0处，但是这样就变成死循环了，所以我们应该退一步，将next数组的第0个赋值为-1，且将整个next数组向后移；就不会变成死循环了；

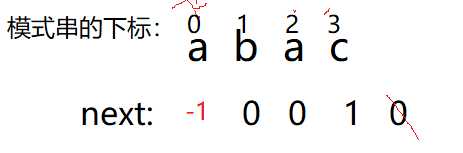
再模拟一次：

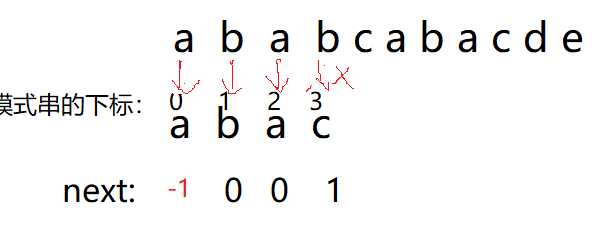
此时不匹配跳next数组；

 

 

 

变成：

发现a不匹配，跳next数组：

 

继续模拟：

发现不匹配，所以此时next应该跳到下标为-1处，但是这里没有下标为-1的，所以实际上就是整体向后移；变成：

 

 

 

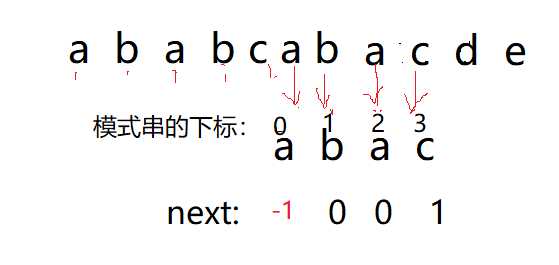
 发现完全匹配了；

那么基于上面的改进，next数组应该怎么写呢：

代码如下：

 1 string s;
 2 string t;
 3 int ssize;
 4 int tsize;
 5 int next1[2000000];
 6         void nextsz(string t,int tsize)
 7         {
 8             next1[0] = -1;     //防止进入死循环，而且到不能匹配时能整体后移
 9             int k = -1;     //是为了调节next数组；
10             int j = 0 ;
11             while(j < tsize-1)
12             {
13             if(k==-1||t[j]==t[k])   //k=-1进入这个循环是为了整体向后移；
14                 {
15                 ++k;         k实际上也是记录了相同的个数；
16                 ++j;
17                 
18                     next1[j] = k;   找到next数组；
19         
20                 }
21                else 
22                 k = next1[k];    //不相同则更新k；
23             }
24 
25         }

现在会了next数组，我们则可以进行模式匹配了；

利用上面求的next数组来进行模式匹配；过程原理和上面画的图是一模一样的；

代码如下：

 

 

 1     int  kmp(string s,string t,int sszie,int tsize)
 2         {
 3             int j = 0;
 4             int i = 0;
 5             while(i<ssize&&j<tsize)
 6         {
 7             
 8                 if(j==-1||s[i]==t[j])  j=-1是为了调节到跳无可跳时，整体向后移；
 9             {
10                 i++;      //匹配整体向前移；
11                 j++;
12                 
13             }
14             else 
15             {
16                  j = next1[j];    不断跳next数组；
17             } 
18 
19             
20         }
21             
22             
23             if(j==tsize)
24             {
25                 return  i-j+1;  //返回模式串在主串的第一个下标；
26             }
27             else return -1；  //不匹配，则返回-1；
28         }

所以这道题的完整代码如下：

代码如下：

 1 #include<iostream>
 2 #include<string.h>
 3 using namespace std ;
 4 
 5 string s;
 6 string t;
 7 int ssize;
 8 int tsize;
 9 int next1[2000000];
10         void nextsz(string t,int tsize)
11         {
12             next1[0] = -1;
13             int k = -1;
14             int j = 0 ;
15             while(j < tsize-1)
16             {
17             if(k==-1||t[j]==t[k])
18                 {
19                 ++k;
20                 ++j;
21                 
22                     next1[j] = k;
23         
24                 }
25                else 
26                 k = next1[k];
27             }
28 
29         }
30         
31         int  kmp(string s,string t,int sszie,int tsize)
32         {
33             int j = 0;
34             int i = 0;
35             while(i<ssize&&j<tsize)
36         {
37             
38                 if(j==-1||s[i]==t[j])
39             {
40                 i++;
41                 j++;
42                 
43             }
44             else 
45             {
46                  j = next1[j];
47             }
48 
49             
50         }
51             
52             
53             if(j==tsize)
54             {
55                 return  i-j+1;
56             }
57             else return 0;
58         }
59         
60         
61 int main()
62 {
63     cin>>s;
64     cin>>t;
65 
66     ssize =  s.size();
67     tsize = t.size();
68         nextsz(t,tsize);
69         cout<<kmp(s,t,ssize,tsize)<<endl;
70 
71         
72     
73 }