初识prufer序列

Posted 2021-02-14 chenxiaoran666

前言

(prufer)序列应该是一个比较实用的东西。

据(hl666)大佬说，一切与度数有关的树上计数问题，都可以用它以及它的性质来解决。

而听说(ZJOI)最近特别喜欢出计数题，所以有必要学一学。

转化(1)：从无根树到(prefur)序列

现在，给你一棵树，我们要考虑如何把它变成(prefur)序列。

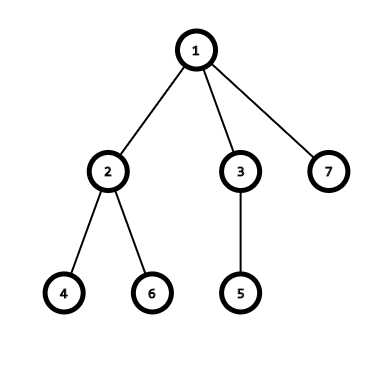
我们需要重复进行以下操作，直至树中只剩下两个点：

• 找到一个度数为(1)，且编号最小的点。（其中编号最小保证了后面将会提到的(prufer)序列的唯一对应性，同时也方便从(prufer)序列转化回无根树）
• 把这个点的父亲节点加入序列，然后把这个点从树中删除。

然后我们就得到了一个长度为(n-2)的序列，这就是(prufer)序列。

所以它有什么实际意义呢？

我也不知道。

以上面的图为例，我们可以模拟这一过程如下：

• 找到(4)号节点，将其父结点加入序列，然后将其删去。此时序列：({2})。
• 找到(5)号节点，将其父结点加入序列，然后将其删去。此时序列：({2,3})。
• 找到(3)号节点，将其父结点加入序列，然后将其删去。此时序列：({2,3,1})。
• 找到(6)号节点，将其父结点加入序列，然后将其删去。此时序列：({2,3,1,2})。
• 找到(2)号节点，将其父结点加入序列，然后将其删去。此时序列：({2,3,1,2,1})。

所以，最后得到的(prufer)序列就是({2,3,1,2,1})。

转化(2)：从(prufer)序列到无根树

还是以刚才那棵树为例吧，我们要考虑如何把它的(prefur)序列变回它本身。

我们需要重复进行以下操作，直至点集中只剩下两个点：（初始化所有点都在点集中）

• 取出(prufer)序列最前面的元素(x)。
• 取出在点集中的、且当前不在(prufer)序列中的最小元素(y)。（这恰好呼应了前面提到过的选取编号最小的节点）
• 在(x,y)之间连接一条边。（注意前面的取出相当于删除）

最后，我们在点集中剩下的两个点中连一条边。

显然这有(n-1)条边，且绝对不会形成环，因此它是一棵树，且就是原树。

以上面的序列为例，我们可以模拟这一过程如下：

• 取出(2,4)连边。此时(prufer)序列：({3,1,2,1})，点集：({1,2,3,5,6,7})。
• 取出(3,5)连边。此时(prufer)序列：({1,2,1})，点集：({1,2,3,6,7})。
• 取出(1,3)连边。此时(prufer)序列：({2,1})，点集：({1,2,6,7})。
• 取出(2,6)连边。此时(prufer)序列：({1})，点集：({1,2,7})。
• 取出(1,2)连边。此时(prufer)序列：({})，点集：({1,7})。

最后再在(1,7)间连边，就可以得到原树了。

(prufer)序列的性质及相关结论

讲了这么多，我们最关键的还是(prufer)序列的一些性质，以及与其有关的一些结论。（毕竟前面也提到过，我也不知道这东西有什么实际意义）

• 重要性质：(prufer)序列与无根树一一对应。

  这应该显然吧，通过前面的介绍应该可以直接得出。

  而由这个性质，我们才能推导出后面的结论。

• 度数为(d_i)的节点会在(prufer)序列中出现(d_i-1)次。

  当某个节点度数为(1)时，会直接被删掉，否则每少掉一个相邻的节点，它就会在序列中出现(1)次。

  因此共出现(d_i-1)次。

• 一个(n)个节点的完全图的生成树个数为(n^{n-2})。

  对于一个(n)个点的无根树，它的(prufer)序列长为(n-2)，而每个位置有(n)种可能性，因此可能的(prufer)序列有(n^{n-2})种。

  又由于(prufer)序列与无根树一一对应，因此生成树个数应与(prufer)序列种树相同，即(n^{n-2})。

• 对于给定度数为(d_{1sim n})的一棵无根树共有(frac{(n-2)!}{prod_{i=1}^n(d_i-1)!})种情况。

  由上面的性质可以知道，度数为(d_i)的节点会在(prufer)序列中出现(d_i-1)次。

  则就是要求出(d_i-1)个(i(1le ile n))的全排列个数。

  而上面那个式子就是可重全排列公式。（即全排列个数除以重复元素内部的全排列个数）

大致就是这些。

例题

下面有两道例题：【洛谷2290】[HNOI2004] 树的计数和【洛谷2624】[HNOI2008] 明明的烦恼。

实际上，这两道题都只用了由(prufer)序列所推导得到的结论，而没有真正构造(prufer)序列，应该也不算特别好的例题。。。