最大子矩形之和
Posted ruangongyouxi
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了最大子矩形之和相关的知识,希望对你有一定的参考价值。
设计思想:这个程序要求在一个二维数组组成的矩形里面找出子矩形,且这个子矩形的和是最大的。我便想着是找出所有的子矩形的和放在一个一维数组里面进行比较,找出最大值。于是便要找一个找出所有子矩形的方法。我首先想到,找到一个数为顶点确定矩形的宽之后逐步改变矩形的长,在改变矩形的宽,在这种宽下改变长。这样便可以找到以这个数为顶点的所有矩形。例如下图的三乘三矩形。以左上角第一个数作为顶点则一共有九个矩形,我也可以得到这些子矩形里面的最大值。下面的问题便是以别的数作为顶点找到它所有的子矩形。我写出了可以使第一排的所有数作为顶点找到以它们为顶点的所有子矩形之和。可是以其他数字为顶点的方法我觉着会不是很好写,便放弃了这种方法。此程序的源代码入下:

源代码:
package 子矩形最大值;
import java.util.Scanner;
public class Main {
public static void Zui(int x,int y,int array[][]) {
int i,j,l;
int cishu=0;
int sum;
int temp;
int max;
int geshu[]=new int[x*y];
for(i=0;i<x;i++) {
sum=0;
for(j=0;j<y;j++) {
System.out.println("第"+cishu+"个子矩形的和为:");
temp=0;
for(l=0;l<i+1;l++) {
temp=temp+array[l][j];
}
sum=sum+temp;
System.out.println(sum);
geshu[cishu]=sum;
cishu++;
}
}
max=geshu[0];
for(l=0;l<cishu;l++) {
if(max<geshu[l]) {
max=geshu[l];
}
}
System.out.println("最大子矩形之和为:"+max);
}
public static void main(String[] args) {
int x,y;
int i,j,k;
@SuppressWarnings("resource")
Scanner scan=new Scanner(System.in);
x=scan.nextInt();
y=scan.nextInt();
int [][] array=new int[x][y];
System.out.println("请输入组成矩形的二维数组:");
for(i=0;i<y;i++) {
for(j=0;j<x;j++) {
array[i][j]=scan.nextInt();
}
}
Zui(x,y,array);
for(k=0;k<(y-1);k++) {
int T[][]=new int[x][y-1-k];
for(i=0;i<x;i++) {
for(j=0;j<(y-1-k);j++) {
T[i][j]=array[i][j+1+k];
}
}
for(i=0;i<x;i++) {
for(j=0;j<(y-1-k);j++) {
System.out.println(T[i][j]);
}
}
Zui(x,(y-1-k),T);
}
}
}
运行测试结果如下:


如上所示,此程序可以计算出以第一行数为顶点的所有子矩形之和。
我上网搜索了这个程序源代码,进行了理解,源代码如下:
package 子矩形最大值网络;
public class Main {
public static void main(String[] args) {
int matrix[][]={{1,-2,3},{-4,5,6},{-7,8,-9}};
maxSum(matrix);
}
public static void maxSum(int matrix[][])
{
if(matrix==null||matrix.length==0)
return;
int max=0;
int col=matrix[0].length,row=matrix.length;
for(int i=0;i<row;i++)
{
int arr[]=new int[col];
for(int j=i;j<row;j++)
{
//遍历所有的子行
for(int k=0;k<col;k++)
{
arr[k]+=matrix[j][k];
//将每子行的值进行相加然后利用子数组的最大和就可以求出子矩阵的最大和
}
for(int l=0;l<col;l++) {
System.out.print(arr[l]+" ");
if((l+1)%3==0) {
System.out.println();
}
}
max=Math.max(max(arr), max);
System.out.println("max为:"+max);
//求出数组的子数组和最大值
}
}
System.out.println(max);
}
public static int max(int arr[])//求最大子数组之和
{
int max=0,sum=0;
for(int i=0;i<arr.length;i++)
{
if(sum<=0)
{
sum=arr[i];
}
else {
sum+=arr[i];
}
max=Math.max(sum, max);
}
return max;
}
}
运行测试结果:
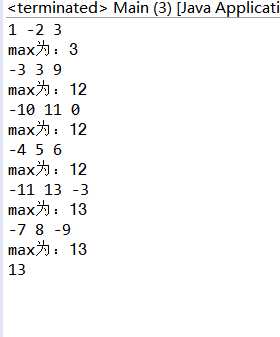
对这个程序进行分析:
这个程序除了主函数之外还有两个函数,一个是max函数,功能是计算出一个一维数组的最大子数组之和。这个功能之前老师有让写,我写的是找出所有子数组取出最大的那个,时间复杂度为O(n方),而我观察了这个函数,它的时间复杂度为O(n)。想法是从第一个数开始往后面累加,每次得到结果都进行比较更新max的值。如果加的结果为正则继续进行求和,若结果为负了,则舍弃这个结果,以下一个数为起点再次进行求和。每次得到结果都要更新max的值。
还有个函数便是求最大子矩形和的函数。想法是首先将第一行看作是一个一维数组,得到其最大子数组,这个最大子数组便是目前的最大子矩形。然后将前两行相加,再得到这前两行相加后构成的一维数组的最大子数组。这便是在宽为2的矩形里面找到最大的子矩形,在与之前宽为1的最大子矩形进行比较,便得到了目前最大的子矩形,这样便可以得到最大子矩形之和。
以上是关于最大子矩形之和的主要内容,如果未能解决你的问题,请参考以下文章