减而治之 - 二分查找 - lower_bound实现原理

Posted 2021-02-14 fyqq0403

       本文介绍利用二分实现 lower_bound 的原理。

       lower_bound(T * a, T & t, int lo, int hi) 的功能是：在某个有序数组 a[lo, hi) 的范围内，查找不小于 t 的最小元素或最小元素位置。这可以用二分来实现。

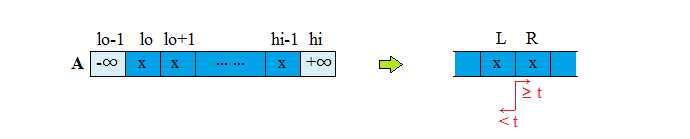
       算法可以这样理解。我们维护两个界限，分别为：

            L：保证 ≤ L 位置的元素都小于 t；
            R：保证 ≥ R 位置的元素都大于等于 t。

       我们不断改变 L 和 R 的位置，使 L 和 R 不断靠近，直至 L + 1 = R 时，R 即为我们要查找的目标位置。

       假想 lo-1 位置存放着一个 -∞ 的哨兵，hi 位置存放着一个 +∞ 的哨兵。初始时 L = lo - 1, R = hi。

       如何调整 L 和 R 的位置呢？每次观察区间 [L, R] 中间位置的元素，即 A[mid = (L+R)/2] 的元素与 t 的大小，因为 A 的有序性：  

            若 A[mid] ≥ t, 我们可以把 R 替换为 mid。
            若 A[mid] < t，我们可以把 L 替换为 mid。
       这样，L 和 R 不断靠近，直至 L + 1 == R，则结束，R 则为我们要找的目标位置。

       C++代码示例（设要查找的类型是整数）：

/* 返回按升序排列的 a[lo, hi) 中不小于 t 的最小值的下标。若不存在，则返回hi */
int lowerBound(int * a, int t, int lo, int hi)
{    
    int L = lo - 1, R = hi;
    while ( L + 1 < R )
    {
        int mid = (L + R) >> 1;
        if ( a[mid] < t )
            L = mid;
        else 
            R = mid;
    }
    
    return R;
}