最短路径算法（II）

Posted 2021-02-14 uninstalllingyi

什么？？你问我为什么不在一篇文章写完所有方法？？
Hmm…其实我是想的，但是博皮的加载速度再带上文章超长图片超多的话…
可能这辈子都打不开了吧…

上接https://www.cnblogs.com/Uninstalllingyi/p/10417446.html

福特算法(Bellman-Ford)

适用范围及时间复杂度

单源最短路径算法，可处理负边权，但，无法处理负回路的情况。时间复杂度O（NE）

N：顶点数，E：边数

核心思想

松弛计算。什么是松弛计算？你戳…

……

好吧我说…

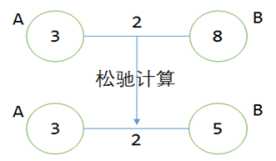松弛计算之前,点B的值是8,但点A的值加上边上的权重2,得到点B的值是5,5<8,更新B为5。这个过程的意义是:找到了一条通向B更短的路线,且该路线先经过A,然后通过权重为2的边,到达点B。

当然，也会存在另一种情况：

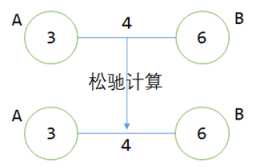在进行松弛计算之前,点B的值是6,点A加上点边上的权值4得到7>6,表示没有找到通向B点更短的路线,故B不需要更新。
这也就诠释了为什么算法不可以处理负权回路的情况。

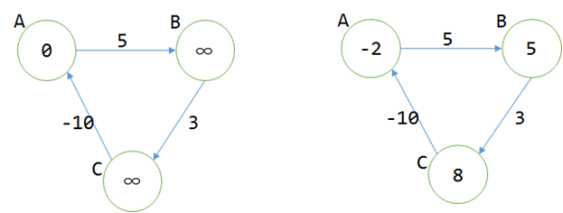
使用松弛之后，发现程序陷入死循环。

代码实现

不难发现，在使用算法前，我们要去检验负权回路。我们需要不断地迭代以求解。

初始化

首先我们需要一个边集数组，暂定u表示起点，v表示终点，w表示权。而这个数组的长度为边的数量。

顶点数*（顶点数-1）/2。

什么？你不知道什么是边集数组？

 1 边集数组
 2 边集数组是利用一维数组存储图中所有边的一种图的表示方法。
 3 该数组中所存储的元素个数要大于等于图中所有的边数。
 4 每个元素用来存储图一条边起点,终点和权值。
 5 struct edge{int s,e;double w;}edges[maxn*(maxn-1)/2];
 6 特别注意的是:如果是无向图,则边的数量=顶点数量*(顶点数量-1)/2,加边函数为:
 7     void addEdges(int u,int v,double w){
 8     edges[++idx].s=u;edges[idx].e=v;edges[idx].w=w;
 9     edges[++idx].e=u;edges[idx].s=v;edges[idx].w=w;
10 }
11 而在枚举边的时候,需要枚举idx条边。
12 定义边集数组时,特别要注意取值范围
13 边集数组是针对边的,如果题目给定了边的数量为n
14 ,那么在无向邻接矩阵中,边集数组要定义为2*n+1,
15 必须考虑来回。如果题目只给定了顶点数p,没有给定边数,
16 则边集数组的取值为:p*(p-1)/2;

悄悄戳进来补课…

 

因为是无向图，算法第一层循环枚举点，第二层枚举边，所以加边函数的定义应是无向图的方法。

算法核心

void bellman(){
    while(--n){
        bool b=false;
        for(int j=1;j<=idx;j++){
            if(dis[edges[j].e]>dis[edges[j].s]+edges[j].w){
                dis[edges[j].e]=dis[edges[j].s]+edges[j].w;
                b=true;
            }
        }
        if(!b){
            break;
        }
    }
} 

View Code