剑指offer面试题 10. 斐波那契数列

Posted 2020-11-04 走在修行的大街上

面试题 10. 斐波那契数列

题目一：求斐波那契数列的第n项

题目描述：求斐波拉契数列的第n项
写出一个函数，输入n,求斐波拉契（Fibonacci）数列的第n项。斐波拉契数列定义如下：

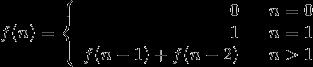
C++ 实现

/* 斐波拉契数列 */
#include <iostream>
using namespace std;
/* 递归实现 */
long long Fibonacci1( unsigned int n )
{
    if ( n <= 1 )
    {
        return(n);
    }
    return(Fibonacci1( n - 1 ) + Fibonacci1( n - 2 ) );
}


/* 非递归实现 */
long long Fibonacci2( unsigned int n )
{
    if ( n <= 1 )
    {
        return(n);
    }
    int f1 = 0, f2 = 1, sum;
    for ( int i = 2; i <= n; i++ )
    {
        sum = f1 + f2;
        f1  = f2;
        f2  = sum;
    }
    return(sum);
}


int main()
{
    /* 测试数据 */
    for ( int i = 0; i <= 20; i++ )
    {
        cout << Fibonacci1( i ) << " ";
    }
    cout << endl;
    for ( int i = 0; i <= 20; i++ )
    {
        cout << Fibonacci2( i ) << " ";
    }
    cout << endl;
    return(0);
}

运行结果

0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765
请按任意键继续. . .

题目二：青蛙跳台阶问题

题目描述：一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
（F(n)=F(n-1)+F(n-2)）

C++ 实现

#include <iostream>
using namespace std;
/* 递归实现 */
long long JumpStairs( unsigned int n )
{
    if ( n <= 1 )
    {
        return(n);
    }
    return(JumpStairs( n - 1 ) + JumpStairs( n - 2 ) );
}


int main()
{
    for ( int i = 1; i <= 20; i++ )
    {
        cout << JumpStairs( i ) << " ";
    }
    cout << endl;
    return(0);
}

运行结果

题目三：变态跳台阶

题目描述：一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。
求该青蛙跳上一个n级的台阶总共有多少种跳法。（F(n)=2*F(n-1)）

C++ 实现

#include <iostream>
using namespace std;
/* 递归实现 */
long long JumpStairs( unsigned int n )
{
    if ( n <= 1 )
    {
        return(1);
    }
    return(2 * JumpStairs( n - 1 ) );
}


int main()
{
    for ( int i = 1; i <= 10; i++ )
    {
        cout << JumpStairs( i ) << " ";
    }
    cout << endl;
    return(0);
}

运行结果

题目四：矩形覆盖

题目描述：我们可以用2×1的小矩形横着或者竖着去覆盖更大的矩形。
请问用n个2×1的小矩形无重叠地覆盖一个2×n的大矩形，总共有多少种方法？

Java 实现

public class Solution {
    public int RectCover(int target) {
        if (target <= 2)
            return target;
        return RectCover(target - 1) + RectCover(target - 2);
    }
}

运行结果

0 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765 10946