第16次CCF CSP认证-第5题-317 号子任务(subtask317)-图论最短路径

Posted 2021-02-13 brainm

【题目背景】
“你在平原上走着走着，突然迎面遇到一堵墙，这墙向上无限高，向下无限深，向
左无限远，向右无限远，这墙是什么？”——《流浪地球》原著
我们带着地球去流浪了，为了处理流浪过程中可能会发生的危机，联合政府找到
你，希望你能协助完成 317 号子任务：制定应急预案。
【题目描述】
地球的表面有 n 个据点，这些据点之间存在 m 条双向道路。
这些据点中，有的是建立在行星发动机之下，受到行星发动机的保护（行星发动机
据点），而其他据点则没有行星发动机的保护（普通据点，比如燃料采集据点/科研据点
等）。
当发生危机的时候，没有行星发动机的保护是非常危险的，所以每个人都需要赶到
最近的行星发动机据点寻求庇护，然而行星发动机据点也不一定安全，再加上行星发动
机据点容量有限，所以有些时候得去第二近或者第三近的行星发动机据点。
联合政府找到你，希望你能够计算出每个据点最近的 k 个行星发动机据点，为了
简化问题，你只需要输出每个据点到最近 k 个行星发动机据点的最短距离之和，如果
某个据点能够到达的行星发动机据点不足 k 个，则输出其能到达的所有行星发动机的
最短距离之和。
【输入格式】
从标准输入读入数据。
输入的第一行包含三个用空格隔开的整数 n, m, k ，含义见题目?述，保证 1 ≤ n ≤
104, 0 ≤ m ≤ 104, 1 ≤ k ≤ 102。据点依次编号为 1 到 n 。
第二行包含 n 个整数依次表示每个据点的类型，每个数为 1 或 0 （1 表示对应据
点为行星发动机据点，0 表示普通据点）。
接下来 m 行，每行三个整数 u, v,w 表示有一条长度为 w 的双向道路连接 u 号据点
和 v 号据点，1 ≤ u, v ≤ n, 1 ≤ w ≤ 103 。
可能有重边和自环。
【输出格式】
输出到标准输出。
输出 n 行，每行输出一个整数表示答案（见题目?述）

【样例 1 输入】
7 6 2
1 0 1 0 1 1 0
1 4 1
1 2 3
2 4 4
2 3 5
2 5 7
6 7 5
【样例 1 输出】

8

8

10

10

0

5

【样例 1 解释】
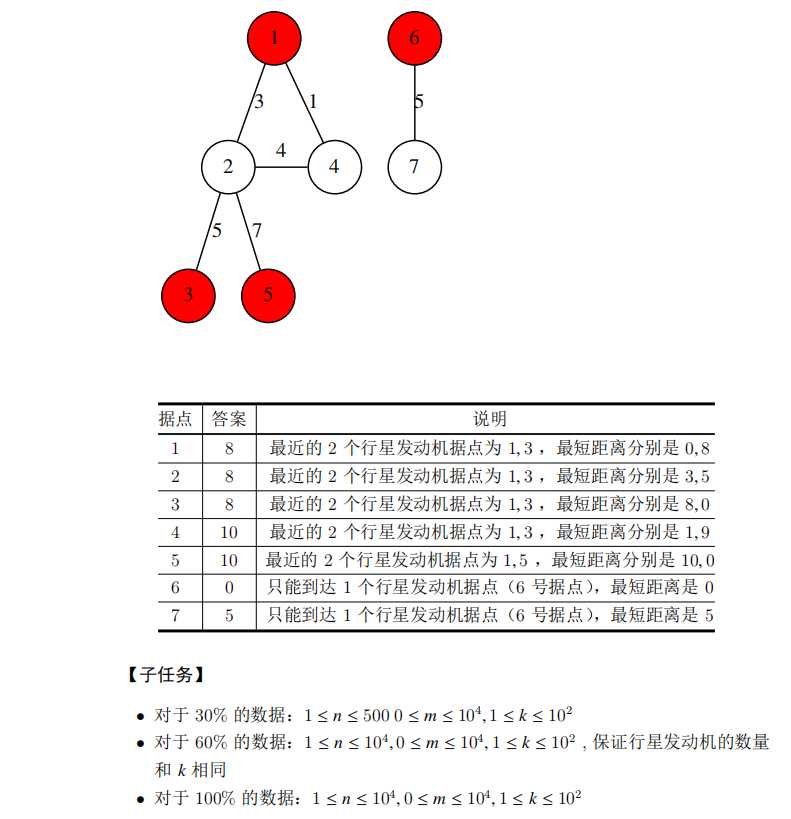
该样例的输入对应的图如下，其中红色点是行星发动机据点，白色点是普通据点。

 

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #define ll long long
 6 using namespace std;
 7 const int amn=1e4+5;
 8 const int inf=9e7;
 9 ll ans[amn];
10 int typ[amn],e[amn][amn],k,n,m;
11 int main()
12 {
13     cin>>n>>m>>k;
14     for(int i=1; i<=n; i++)
15     {
16         for(int j=1; j<=n; j++)
17         {
18             if(i==j)e[i][j]=0;
19             else e[i][j]=inf;
20         }
21     }
22     for(int i=1; i<=n; i++)
23     {
24         int tt;
25         cin>>tt;
26         typ[i]=tt;
27     }
28     int u,v,w;
29     for(int i=1; i<=m; i++)
30     {
31         cin>>u>>v>>w;
32         e[u][v]=w;
33         e[v][u]=w;
34     }
35     for(int c=1; c<=n; c++)
36     {
37         for(int i=1; i<=n; i++)
38         {
39             for(int j=1; j<=n; j++)
40                 if(e[i][k]<inf&&e[k][j]<inf&&e[i][j]>e[i][c]+e[c][j])
41                     e[i][j]=e[i][c]+e[c][j];
42         }
43     }
44 //    cout<<endl<<endl;///查看图的最短路径(调试用)
45 //    for(int i=1; i<=n; i++)
46 //    {
47 //        for(int j=1; j<=n; j++)
48 //        {
49 //            printf("%10d",e[i][j]);
50 //        }
51 //        cout<<endl<<endl;
52 //    }
53     for(int i=1; i<=n; i++)
54     {
55         int top=0;
56         memset(ans,0,sizeof(ans));
57         for(int j=1; j<=n; j++)
58         {
59             if(e[i][j]<inf&&typ[j])
60             {
61                 ans[top++]=e[i][j];
62             }
63         }
64         sort(ans,ans+top);
65         ll sum=0;
66         for(int i=0; i<k&&i<top; i++)
67         {
68             sum+=ans[i];
69         }
70         cout<<sum<<endl;
71     }
72     return 0;
73 }
74 /*
75 样例
76 
77 7 6 2
78 1 0 1 0 1 1 0
79 1 4 1
80 1 2 3
81 2 4 4
82 2 3 5
83 2 5 7
84 6 7 5
85 
86 */