最小生成树

Posted 2021-02-13 qf-breeze

//kruskal
struct EDGE{
    LL u,v,w;
}edge[200000+5];
LL n,m,ans,eu,ev,cnt=0;
LL fa[5000+5];
inline bool cmp(EDGE a,EDGE b){
    return a.w<b.w;
}
inline LL find(LL x) {
    while(x!=fa[x]) x=fa[x]=fa[fa[x]];
    return x;
}
inline void kruskal() {
    sort(edge+1,edge+m+1,cmp);
    for(register int i=1;i<=m;i++) {
        eu=find(edge[i].u) , ev=find(edge[i].v);
        if(eu == ev) continue ;
        ans += edge[i].w ;
        fa[ev]=eu;
        if(++cnt == n-1) break ;
    }
    return ;
}

kruskal是按权值排序的贪心算法

众所周知 n个点 靠n-1条边就可以连通了。。

带上权值 就可以连成一棵最小生成树。

其实 并查集的操作就是判重。。（不知道咋解释） 合并之后就不会重复选中了。

 

 

 

prim的话

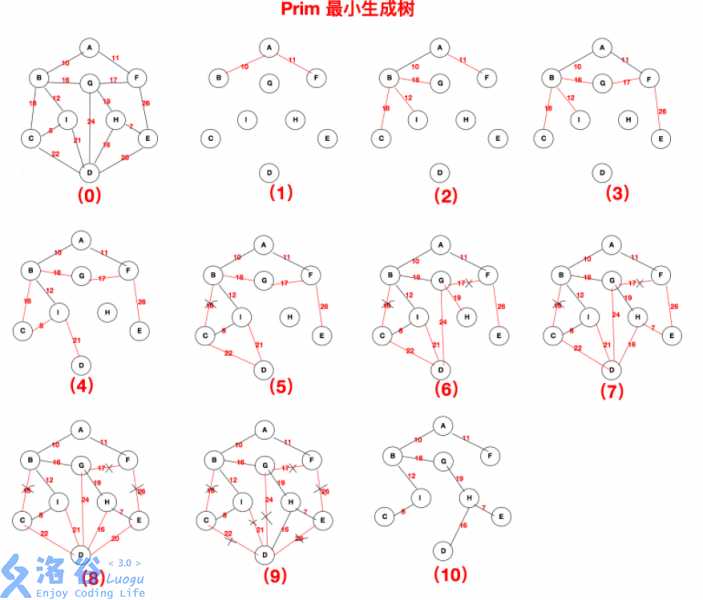
prim的话 有好几种版本。。

#include<cstdio>
#include<cstdlib>
#include<iostream>

using namespace std;
/*最小生成树Prim未优化版*/

int book[100];//用于记录这个点有没有被访问过
int dis[100];//用于记录距离树的距离最短路程
int MAX = 99999;//边界值
int maps[100][100];//用于记录所有边的关系

int main()
{
    int i,j,k;//循环变量
    int n,m;//输入的N个点，和M条边
    int x,y,z;//输入变量
    int min,minIndex;
    int sum=0;//记录最后的答案

    cin>>n>>m;

    //初始化maps，除了自己到自己是0其他都是边界值
    for (i = 1; i <= n; i++)
    {
        for (j = 1; j <= n; j++)
        {
            if(i!=j)
                maps[i][j] = MAX;
            else
                maps[i][j] = 0;
        }
    }

    for (i = 1; i <= m; i++)
    {
        cin>>x>>y>>z;//输入的为无向图
        maps[x][y] = z;
        maps[y][x] = z;
    }

    //初始化距离数组，默认先把离1点最近的找出来放好
    for (i = 1; i <= n; i++)
        dis[i] = maps[1][i];

    book[1]=1;//记录1已经被访问过了

    for (i = 1; i <= n-1; i++)//1已经访问过了，所以循环n-1次
    {
        min = MAX;//对于最小值赋值，其实这里也应该对minIndex进行赋值，但是我们承认这个图一定有最小生成树而且不存在两条相同的边
        //寻找离树最近的点
        for (j = 1; j <= n; j++)
        {
            if(book[j] ==0 && dis[j] < min)
            {
                min = dis[j];
                minIndex = j;
            }
        }

        //记录这个点已经被访问过了
        book[minIndex] = 1;
        sum += dis[minIndex];

        for (j = 1; j <= n; j++)
        {
            //如果这点没有被访问过，而且这个点到任意一点的距离比现在到树的距离近那么更新
            if(book[j] == 0 && maps[minIndex][j] < dis[j])
                dis[j] = maps[minIndex][j];
        }
    }

    cout<<sum<<endl;
}

#include<bits/stdc++.h>//链式前向星优化
using namespace std;
#define re register
#define il inline
il int read()
{
    re int x=0,f=1;char c=getchar();
    while(c<‘0‘||c>‘9‘){if(c==‘-‘) f=-1;c=getchar();}
    while(c>=‘0‘&&c<=‘9‘) x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return x*f;
}//快读，不理解的同学用cin代替即可
#define inf 123456789
#define maxn 5005
#define maxm 200005
struct edge
{
    int v,w,next;
}e[maxm<<1];
//注意是无向图，开两倍数组
int head[maxn],dis[maxn],cnt,n,m,tot,now=1,ans;
//已经加入最小生成树的的点到没有加入的点的最短距离，比如说1和2号节点已经加入了最小生成树，那么dis[3]就等于min(1->3,2->3)
bool vis[maxn];
//链式前向星加边
il void add(int u,int v,int w)
{
    e[++cnt].v=v;
    e[cnt].w=w;
    e[cnt].next=head[u];
    head[u]=cnt;
}
//读入数据
il void init()
{
    n=read(),m=read();
    for(re int i=1,u,v,w;i<=m;++i)
    {
        u=read(),v=read(),w=read();
        add(u,v,w),add(v,u,w);
    }
}
il int prim()
{
    //先把dis数组附为极大值
    for(re int i=2;i<=n;++i)
    {
        dis[i]=inf;
    }
    //这里要注意重边，所以要用到min
    for(re int i=head[1];i;i=e[i].next)
    {
        dis[e[i].v]=min(dis[e[i].v],e[i].w);
    }
    while(++tot<n)//最小生成树边数等于点数-1
    {
        re int minn=inf;//把minn置为极大值
        vis[now]=1;//标记点已经走过
        //枚举每一个没有使用的点
        //找出最小值作为新边
        //注意这里不是枚举now点的所有连边，而是1~n
        for(re int i=1;i<=n;++i)
        {
            if(!vis[i]&&minn>dis[i])
            {
                minn=dis[i];
                now=i;
            }
        }
        ans+=minn;
        //枚举now的所有连边，更新dis数组
        for(re int i=head[now];i;i=e[i].next)
        {
            re int v=e[i].v;
            if(dis[v]>e[i].w&&!vis[v])
            {
                dis[v]=e[i].w;
            }
        }
    }
    return ans;
}
int main()
{
    init();
    printf("%d",prim());
    return 0;
}

#include<cstdio>//堆优化版的prim
#include<queue>
#include<cstring>
#include<algorithm>
#define R register int
using namespace std;

int k,n,m,cnt,sum,ai,bi,ci,head[5005],dis[5005],vis[5005];

struct Edge
{
    int v,w,next;
}e[400005];

void add(int u,int v,int w)
{
    e[++k].v=v;
    e[k].w=w;
    e[k].next=head[u];
    head[u]=k;
}

typedef pair <int,int> pii;
priority_queue <pii,vector<pii>,greater<pii> > q;

void prim()
{
    dis[1]=0;
    q.push(make_pair(0,1));
    while(!q.empty()&&cnt<n)
    {
        int d=q.top().first,u=q.top().second;
        q.pop();
        if(vis[u]) continue;
        cnt++;
        sum+=d;
        vis[u]=1;
        for(R i=head[u];i!=-1;i=e[i].next)
            if(e[i].w<dis[e[i].v])
                dis[e[i].v]=e[i].w,q.push(make_pair(dis[e[i].v],e[i].v));
    }
}

int main()
{
    memset(dis,127,sizeof(dis));
    memset(head,-1,sizeof(head));
    scanf("%d%d",&n,&m);
    for(R i=1;i<=m;i++)
    {
        scanf("%d%d%d",&ai,&bi,&ci);
        add(ai,bi,ci);
        add(bi,ai,ci);
    }
    prim();
    if (cnt==n)printf("%d",sum);
    else printf("orz");
}

prim不如kruskal 如果说要是稠密图【比较少的吧】

就用prim

其实prim的优化挺快的吧

emm