模拟棋盘法计算遗传中概率
Posted zylak
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了模拟棋盘法计算遗传中概率相关的知识,希望对你有一定的参考价值。
#include<cstdio> #include<cstring> using namespace std; int m[5][5],w[3][3],s[10],b[3][3],c[5],ans[10][10]; char fa[100],ma[100],qu[100]; int gcd(int a,int b) { return b?gcd(b,a%b):a; } int main() { int tar; printf("请输入亲本基因类型: "); printf("父本:"); scanf("%s",fa); printf(" "); for (int i=0;i<strlen(fa);i++) if (fa[i]==‘M‘) b[1][1]++; else if (fa[i]==‘m‘) b[1][2]++; else if (fa[i]==‘X‘ && fa[i+2]==‘A‘) m[1][1]++,i+=3; else if (fa[i]==‘X‘ && fa[i+2]==‘a‘) m[1][2]++,i+=3; else if (fa[i]==‘Y‘ && fa[i+2]==‘A‘) m[2][1]++,i+=3; else if (fa[i]==‘Y‘ && fa[i+2]==‘a‘) m[2][2]++,i+=3; printf("母本:"); scanf("%s",ma); printf(" "); for (int i=0;i<strlen(ma);i++) if (ma[i]==‘M‘) b[2][1]++; else if (ma[i]==‘m‘) b[2][2]++; else if (ma[i]==‘X‘ && ma[i+2]==‘A‘) w[1][1]++,i+=3; else if (ma[i]==‘X‘ && ma[i+2]==‘a‘) w[1][2]++,i+=3; printf("请输入第几代:"); scanf("%d",&tar); printf(" "); for (int i=1;i<=tar;i++) { s[1]=m[1][1]*w[1][1]; s[2]=m[1][2]*w[1][1]+m[1][1]*w[1][2]; s[3]=m[1][2]*w[1][2]; s[4]=m[2][1]*w[1][1]; s[5]=m[2][2]*w[1][1]; s[6]=m[2][1]*w[1][2]; s[7]=m[2][2]*w[1][2]; c[1]=b[1][1]*b[2][1]; c[2]=b[1][1]*b[2][2]+b[1][2]*b[2][1]; c[3]=b[1][2]*b[2][2]; for (int j=1;j<=3;j++) for (int k=1;k<=7;k++) ans[j][k]=c[j]*s[k]; int ggcd; m[1][1]=ans[1][4]+ans[2][4]+ans[3][4]+ans[1][5]+ans[2][5]+ans[3][5]; m[1][2]=ans[1][6]+ans[2][6]+ans[3][6]+ans[1][7]+ans[2][7]; ggcd=gcd(m[1][1],m[1][2]); m[2][1]=ans[1][4]+ans[2][4]+ans[3][4]+ans[1][6]+ans[2][6]+ans[3][6]; ggcd=gcd(ggcd,m[2][1]); m[2][2]=ans[1][5]+ans[2][5]+ans[3][5]+ans[1][7]+ans[2][7]; ggcd=gcd(ggcd,m[2][2]); m[1][1]/=ggcd; m[1][2]/=ggcd; m[2][1]/=ggcd; m[2][2]/=ggcd; w[1][1]=(ans[1][1]+ans[2][1]+ans[3][1])*2+ans[1][2]+ans[2][2]+ans[3][2]; w[1][2]=ans[1][2]+ans[2][2]+ans[3][2]+(ans[1][3]+ans[2][3])*2; ggcd=gcd(w[1][1],w[1][2]); w[1][1]/=ggcd; w[1][2]/=ggcd; b[1][1]=c[1]*2+c[2],b[2][1]=c[1]*2+c[2]; b[1][2]=c[3]*2+c[2],b[2][2]=c[3]*2+c[2]; ggcd=gcd(b[1][1],b[1][2]); b[1][1]/=ggcd; b[1][2]/=ggcd; } int sum=0; for (int i=1;i<=3;i++) for (int j=1;j<=7;j++) sum+=ans[i][j]; printf("请输入所求基因型:"); scanf("%s",qu); printf(" "); if (qu[0]==‘M‘ && qu[1]==‘M‘ && qu[2]==‘X‘ && qu[4]==‘A‘ && qu[6]==‘X‘ && qu[8]==‘A‘) printf("所占比例:%d/%d",ans[1][1]/(gcd(ans[1][1],sum)),sum/(gcd(ans[1][1],sum))); if (qu[0]==‘M‘ && qu[1]==‘M‘ && qu[2]==‘X‘ && qu[4]==‘A‘ && qu[6]==‘X‘ && qu[8]==‘a‘) printf("所占比例:%d/%d",ans[1][2]/(gcd(ans[1][2],sum)),sum/(gcd(ans[1][2],sum))); if (qu[0]==‘M‘ && qu[1]==‘M‘ && qu[2]==‘X‘ && qu[4]==‘a‘ && qu[6]==‘X‘ && qu[8]==‘a‘) printf("所占比例:%d/%d",ans[1][3]/(gcd(ans[1][3],sum)),sum/(gcd(ans[1][3],sum))); if (qu[0]==‘M‘ && qu[1]==‘M‘ && qu[2]==‘X‘ && qu[4]==‘A‘ && qu[6]==‘Y‘ && qu[8]==‘A‘) printf("所占比例:%d/%d",ans[1][4]/(gcd(ans[1][4],sum)),sum/(gcd(ans[1][4],sum))); if (qu[0]==‘M‘ && qu[1]==‘M‘ && qu[2]==‘X‘ && qu[4]==‘A‘ && qu[6]==‘Y‘ && qu[8]==‘a‘) printf("所占比例:%d/%d",ans[1][5]/(gcd(ans[1][5],sum)),sum/(gcd(ans[1][5],sum))); if (qu[0]==‘M‘ && qu[1]==‘M‘ && qu[2]==‘X‘ && qu[4]==‘a‘ && qu[6]==‘Y‘ && qu[8]==‘A‘) printf("所占比例:%d/%d",ans[1][6]/(gcd(ans[1][6],sum)),sum/(gcd(ans[1][6],sum))); if (qu[0]==‘M‘ && qu[1]==‘M‘ && qu[2]==‘X‘ && qu[4]==‘a‘ && qu[6]==‘Y‘ && qu[8]==‘a‘) printf("所占比例:%d/%d",ans[1][7]/(gcd(ans[1][7],sum)),sum/(gcd(ans[1][7],sum))); if (qu[0]==‘M‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘A‘ && qu[6]==‘X‘ && qu[8]==‘A‘) printf("所占比例:%d/%d",ans[2][1]/(gcd(ans[2][1],sum)),sum/(gcd(ans[2][1],sum))); if (qu[0]==‘M‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘A‘ && qu[6]==‘X‘ && qu[8]==‘a‘) printf("所占比例:%d/%d",ans[2][2]/(gcd(ans[2][2],sum)),sum/(gcd(ans[2][2],sum))); if (qu[0]==‘M‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘a‘ && qu[6]==‘X‘ && qu[8]==‘a‘) printf("所占比例:%d/%d",ans[2][3]/(gcd(ans[2][3],sum)),sum/(gcd(ans[2][3],sum))); if (qu[0]==‘M‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘A‘ && qu[6]==‘Y‘ && qu[8]==‘A‘) printf("所占比例:%d/%d",ans[2][4]/(gcd(ans[2][4],sum)),sum/(gcd(ans[2][4],sum))); if (qu[0]==‘M‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘A‘ && qu[6]==‘Y‘ && qu[8]==‘a‘) printf("所占比例:%d/%d",ans[2][5]/(gcd(ans[2][5],sum)),sum/(gcd(ans[2][5],sum))); if (qu[0]==‘M‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘a‘ && qu[6]==‘Y‘ && qu[8]==‘A‘) printf("所占比例:%d/%d",ans[2][6]/(gcd(ans[2][6],sum)),sum/(gcd(ans[2][6],sum))); if (qu[0]==‘M‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘a‘ && qu[6]==‘Y‘ && qu[8]==‘a‘) printf("所占比例:%d/%d",ans[2][7]/(gcd(ans[2][7],sum)),sum/(gcd(ans[2][7],sum))); if (qu[0]==‘m‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘A‘ && qu[6]==‘X‘ && qu[8]==‘A‘) printf("所占比例:%d/%d",ans[3][1]/(gcd(ans[3][1],sum)),sum/(gcd(ans[3][1],sum))); if (qu[0]==‘m‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘A‘ && qu[6]==‘X‘ && qu[8]==‘a‘) printf("所占比例:%d/%d",ans[3][2]/(gcd(ans[3][2],sum)),sum/(gcd(ans[3][2],sum))); if (qu[0]==‘m‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘a‘ && qu[6]==‘X‘ && qu[8]==‘a‘) printf("所占比例:%d/%d",ans[3][3]/(gcd(ans[3][3],sum)),sum/(gcd(ans[3][3],sum))); if (qu[0]==‘m‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘A‘ && qu[6]==‘Y‘ && qu[8]==‘A‘) printf("所占比例:%d/%d",ans[3][4]/(gcd(ans[3][4],sum)),sum/(gcd(ans[3][4],sum))); if (qu[0]==‘m‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘A‘ && qu[6]==‘Y‘ && qu[8]==‘a‘) printf("所占比例:%d/%d",ans[3][5]/(gcd(ans[3][5],sum)),sum/(gcd(ans[3][5],sum))); if (qu[0]==‘m‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘a‘ && qu[6]==‘Y‘ && qu[8]==‘A‘) printf("所占比例:%d/%d",ans[3][6]/(gcd(ans[3][6],sum)),sum/(gcd(ans[3][6],sum))); if (qu[0]==‘m‘ && qu[1]==‘m‘ && qu[2]==‘X‘ && qu[4]==‘a‘ && qu[6]==‘Y‘ && qu[8]==‘a‘) printf("所占比例:%d/%d",ans[3][7]/(gcd(ans[3][7],sum)),sum/(gcd(ans[3][7],sum))); return 0; }
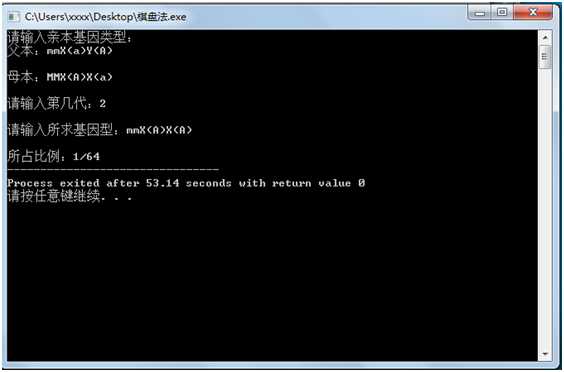
以上是关于模拟棋盘法计算遗传中概率的主要内容,如果未能解决你的问题,请参考以下文章