HDU 1232 畅通工程

Posted 2021-02-12 happy-medge

题面：

传送门

畅通工程

Input ?le: standard input

Output ?le: standard output

Time limit: 2 second

Memory limit: 256 megabytes

 

某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？ 

 

Input

测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。 
注意:两个城市之间可以有多条道路相通,也就是说
3 3
1 2
1 2
2 1
这种输入也是合法的
当N为0时，输入结束，该用例不被处理。 

 

Output

对每个测试用例，在1行里输出最少还需要建设的道路数目。 

 

Example

Input

4 2

1 3

4 3

3 3

1 2

1 3

2 3

5 2

1 2

3 5

999 0

0

Output

1

0

2

998 

 

Hint

Huge input, scanf is recommended.

题目分析：

这题是经典的考察并查集的内容：我们还是先分析一下题目：其实就是题目会给出类似这样的图（由点：城市；线：道路 组成）：

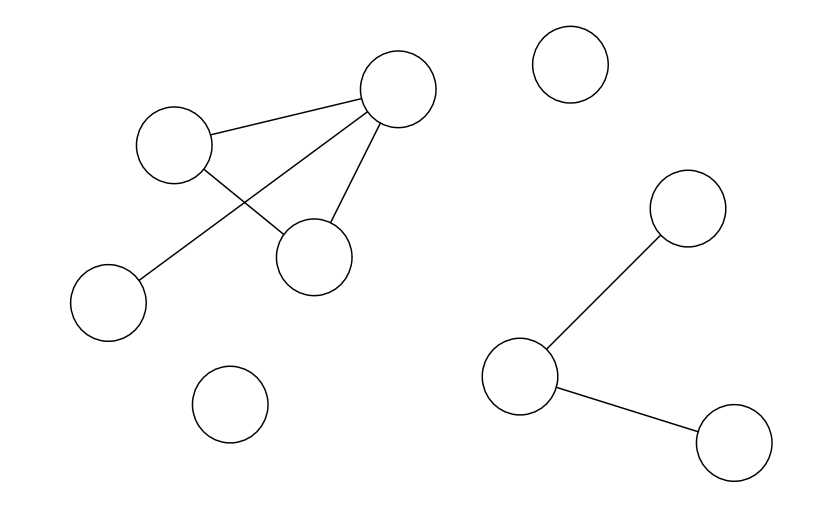
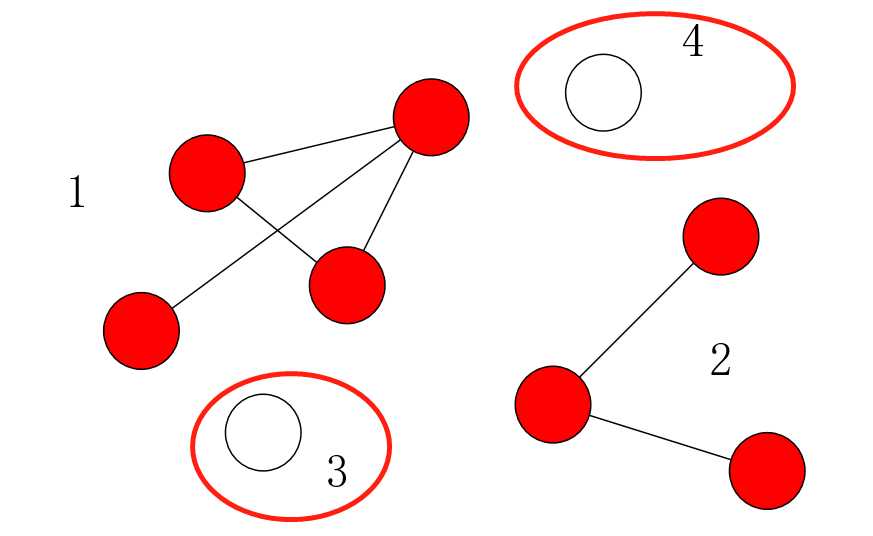
这幅图给出了n个点和它们的连通关系，然后要找有多少个“独立”的图，也就是有多少个强连通图（一个图强连通意味着这个图中的点都可以两两互相到达，一个“独立”的点也算）：

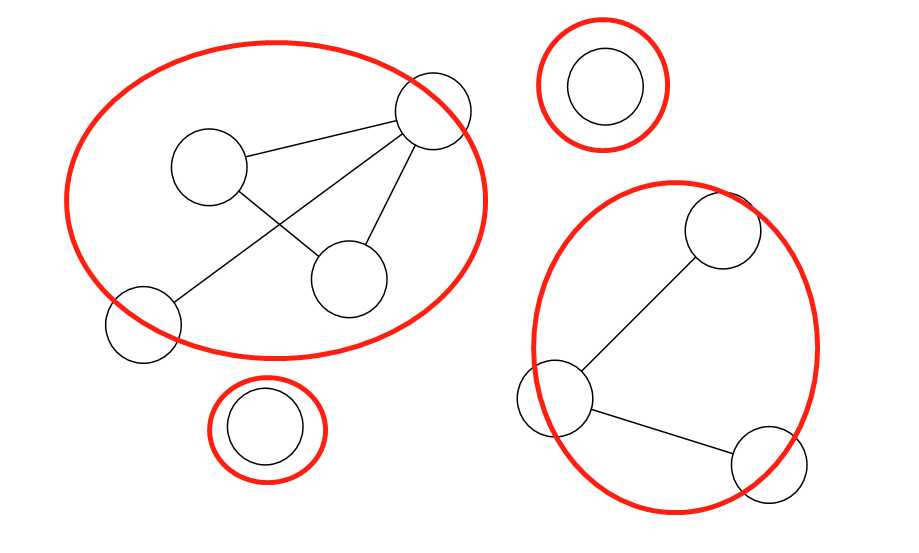
显然，这里有4个强连通图。如果要把它们全部连通，就只需要4-1条道路就可以了（一条道路是双向的）：

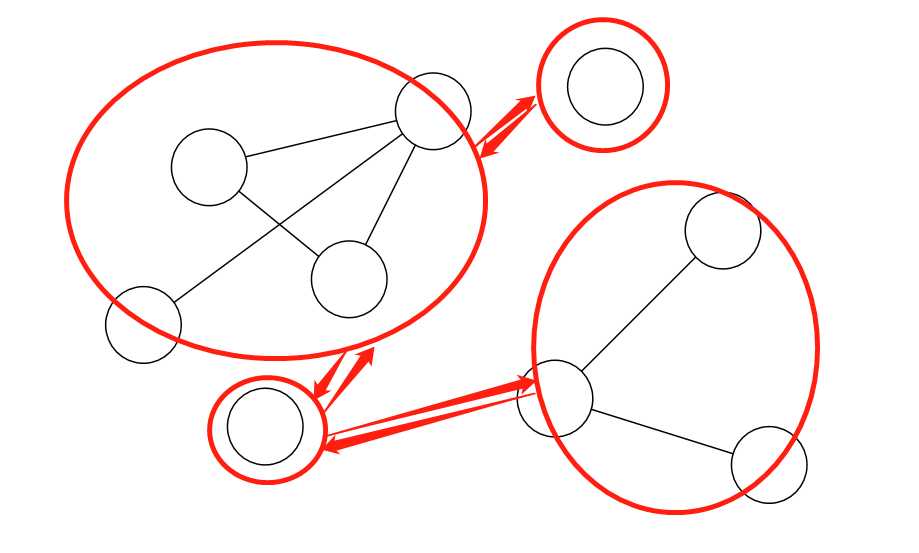
所以，这道题的关键就是如何求这些“独立”的图。首先，自然的想法当然是搜索（从有道路连接的点搜索，也就是把这些“独立”的图理解为连通块）：

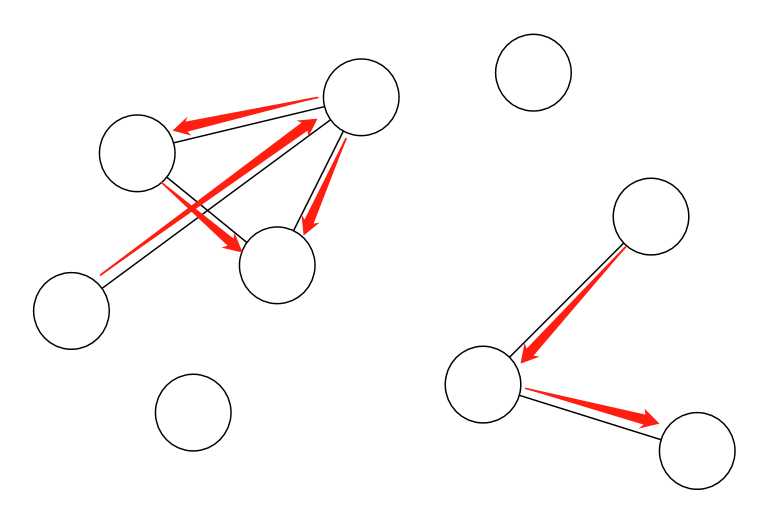
然后标记和计数：

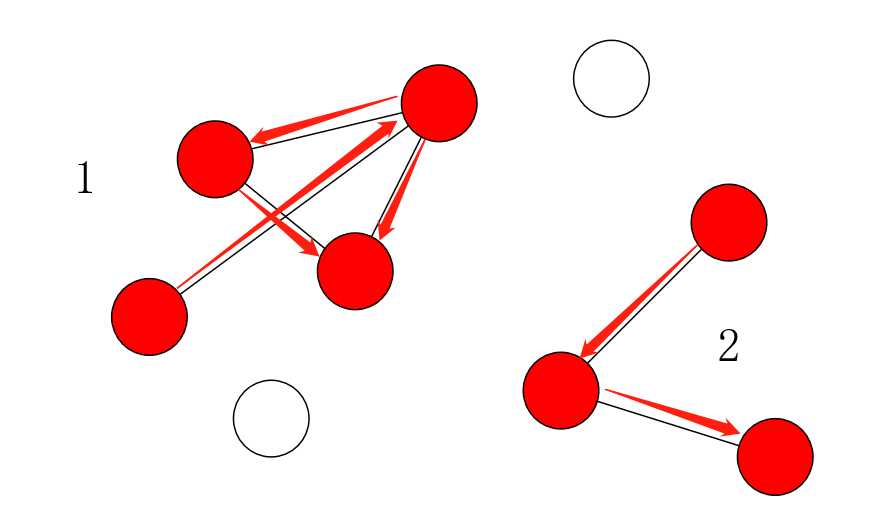
剩下没道路的点就是未被标记的点，这时我们只需要统计一遍未标记的点就行了：

 

 

AC代码：

 1 #include <cstdio>
 2 #include <cstring>
 3 using namespace std;
 4 int n, m;
 5 int G[1005][1005];
 6 int vis[1005];     //标记数组
 7 int is[1005];      //有道路连接的点
 8 
 9 void dfs(int u){
10     if(vis[u]) return;   //被访问过就进行回溯
11     vis[u] = 1;          //标记
12     for(int i = 1; i <= 1000; i++){
13         if(G[u][i]) dfs(i);    
14     }
15 }
16 
17 int main(){
18     int u, v;
19     while(~scanf("%d", &n) && n){
20         scanf("%d", &m);
21         memset(G, 0, sizeof(G));
22         memset(vis, 0, sizeof(vis));
23         memset(is, 0, sizeof(is));
24 
25         for(int i = 0; i < m; i++){
26             scanf("%d%d", &u, &v);
27             G[u][v] = G[v][u] = 1;   //双向的路
28             is[u] = is[v] = 1;       
29         }
30 
31         int cnt = 0;     //计数
32         for(int i = 1; i <= n; i++){
33             if(is[i] && !vis[i]){   //有道路连接并且没被访问过
34                 dfs(i);   //进行搜索
35                 cnt++;   
36             }
37         }
38 
39         for(int i = 1; i <= n; i++){
40             if(!vis[i]) cnt++;      //统计独立的点
41         }
42 
43         printf("%d
", cnt-1);
44     }
45     return 0;
46 }

 

邻接表版本：

 1 #include <cstdio>
 2 #include <cstring>
 3 #include <vector>
 4 using namespace std;
 5 int n, m;
 6 vector<int> G[1005];   //邻接表
 7 int vis[1005];     //标记数组
 8 int is[1005];      //有道路连接的点
 9 
10 void dfs(int u){
11     if(vis[u]) return;   //被访问过就进行回溯
12     vis[u] = 1;          //标记
13     for(int i = 0; i < G[u].size(); i++) dfs(G[u][i]);
14 }
15 
16 int main(){
17     int u, v;
18     while(~scanf("%d", &n) && n){
19         scanf("%d", &m);
20         for(int i = 0; i < 1005; i++){
21             G[i].clear();
22         }
23         memset(vis, 0, sizeof(vis));
24         memset(is, 0, sizeof(is));
25 
26         for(int i = 0; i < m; i++){
27             scanf("%d%d", &u, &v);
28             G[u].push_back(v);
29             G[v].push_back(u);   //双向的路
30             is[u] = is[v] = 1;
31         }
32 
33         int cnt = 0;     //计数
34         for(int i = 1; i <= n; i++){
35             if(is[i] && !vis[i]){   //有道路连接并且没被访问过
36                 dfs(i);   //进行搜索
37                 cnt++;
38             }
39         }
40 
41         for(int i = 1; i <= n; i++){
42             if(!vis[i]) cnt++;      //统计独立的点
43         }
44 
45         printf("%d
", cnt-1);
46     }
47     return 0;
48 }

 

那这道题和并查集有什么关系？我们再看回我们之前求的是什么：有多少个“独立”的图？这些图是不是很像集合？一个“独立”的图对应一个“集合”；并查集的“查”，就是查一个点的所属集合，而“并”，就是合并两个集合。这里我们用的是一边“查”，一边“并”的做法。原因在于：题目会输入这样的数据：1 2    2 1  ，很明显这是相同的道路。如果我们没有一边“查”，一边“并”，我们的并查集数组对于这种数据就会出bug。对于并查集，“查”的过程我们可以进行状态压缩，使以后查的速度加快。统计集合的个数有两种方法：标记数组法和直接查找法。标记数组法就是：在“查”每一个点的集合编号的同时，标记集合的编号，然后通过遍历标记数组统计集合数目。直接查找法就是：直接遍历并查集数组。如果下标等于数组自身的值，那么就是一个集合，所以直接统计有多少个下标等于数组自身的值就有多少个集合。建议使用后者，因为不用多开一个数组。

 

 

AC代码：

 1 #include <cstdio>
 2 #include <cstring>
 3 using namespace std;
 4 int road[1005];
 5 
 6 int fd(int u){
 7     int r = u;
 8     while(road[r] != r){
 9         r = road[r];     //查
10     }
11 
12     int i = u;
13     int next;
14     while(i != r){      //状态压缩
15         next = road[i];
16         road[i] = r;
17         i = next;
18     }
19     return r;
20 }
21 
22 int main(){
23     int n;
24     while(scanf("%d", &n) == 1 && n){
25         int m;
26         scanf("%d", &m);
27         memset(road, 0, sizeof(road));
28         for(int i = 1; i <= n; i++){
29             road[i] = i;    //初始化并查集数组
30         }
31 
32         int a, b;
33         int a1, b1;
34         while(m--){
35             scanf("%d%d", &a, &b);
36             a1 = fd(a);    //查
37             b1 = fd(b);
38             if(a1 != b1){   //不属于同一个集合就并
39                 road[a1] = b1;
40             }
41         }
42 
43         int cnt = 0;
44         for(int i = 1; i <= n; i++){
45             if(road[i] == i) cnt++;
46         }
47 
48         printf("%d
", cnt-1);
49     }
50     return 0;
51 }