两段法

Posted 2021-02-12 fangxiaoqi

　　如果LP问题的系数矩阵不含单位矩阵作初始基，那么就可以两段法求解。

 

　　拖出一题：

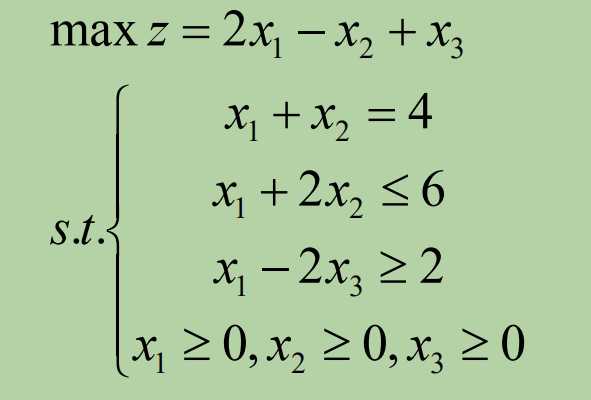
　　首先，我们按照单纯形法解题的思路一开始先去化出标准型：

关于单纯形法，可以参考我的这篇博客：https://www.cnblogs.com/fangxiaoqi/p/10493527.html

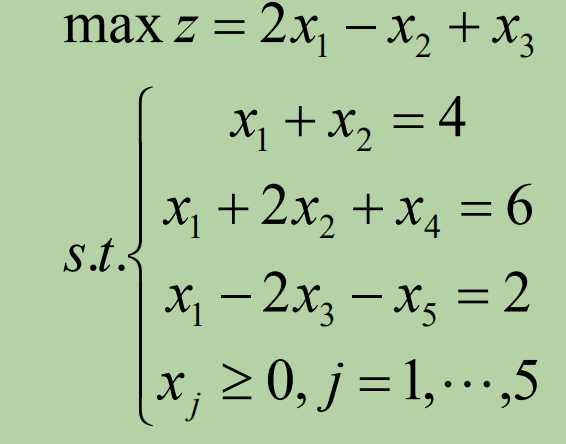
对应的增广矩阵：

1	1	0	0	0	4
1	2	0	1	0	6
1	0	-2	0	-1	2

　　我们发现：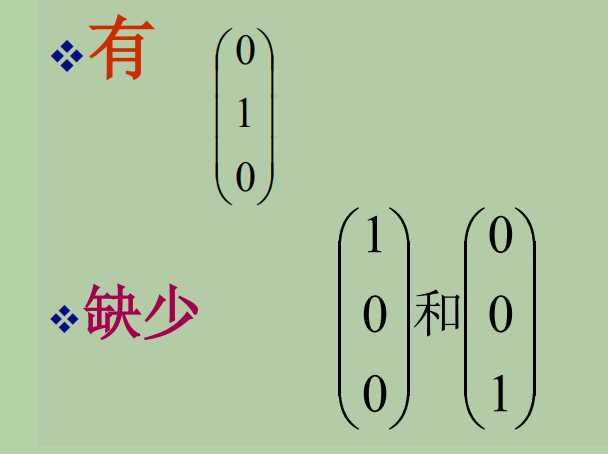

　　这就很尴尬了，没有单位矩阵，算起来可麻烦廖~~~

　　这里就要用到我们的两段法了！

阶段1：添加人工变量, 构造辅助规划

　　我们添加人工变量x6，x7。再从另外5个里选一个，这不就有了单位矩阵啦？而对应的辅助规划目标函数是：人工变量之和等于零。

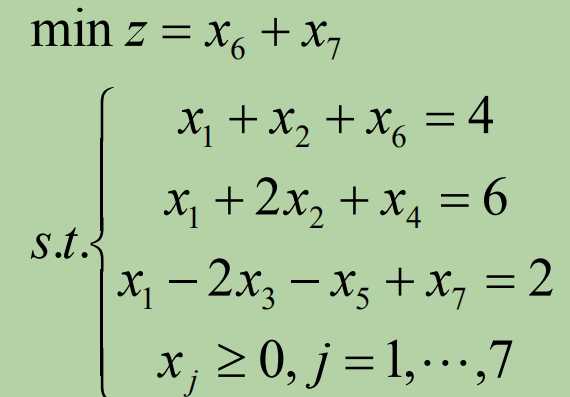
　　目标函数经过行变换使基变量系数全部化为0。

 

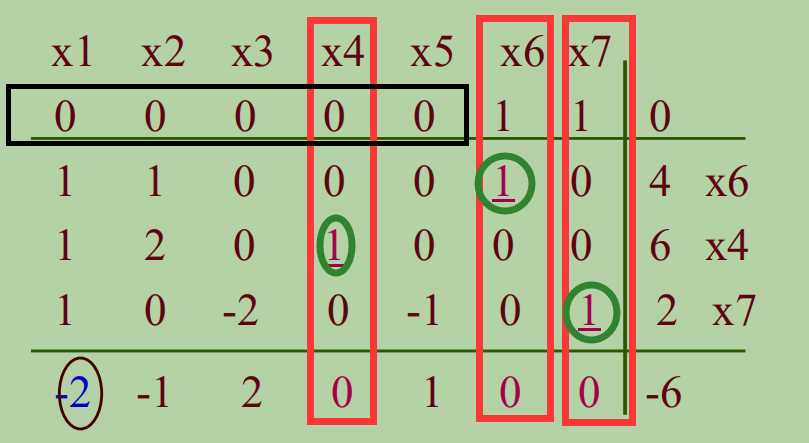
　　其实，如果我们仔细观察的话，目标函数还可以减少，所以当前解并不是最优解。

存在负检验数，说明目标函数还可以减少

 　　于是乎，我们选择x1作为换入变量，将基变量所在列化为单位矩阵的列。

　　然后根据最小比值法则，选x1的第三行的1作主元。令X7出基，而且我们知道x7对应的比值最小，所以是换出变量。

 

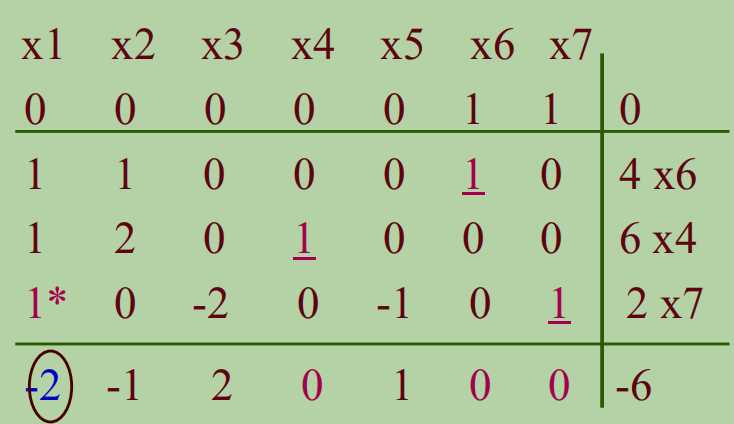
• ①主元所在行乘以适当倍数使主元变成1

• ②其他行与主元所在行作行变换使主元所在列成为单位矩阵里的列

　　就变成酱紫了：

　　but！仍然：存在负检验数，说明目标函数还可以减少，还是没有找到最优解。

　　选x3进基,再次迭代。

　　再次历经上面的①和②：

　　然后，

　　我们到这里，没有发现小于0的检验数，这就说明了目标函数值不可能再减少，我们就可以通过辅助规划找到最优解。

注：

如果辅助规划最优表人工变量已全部出基，则可以转入阶段2。(引入人工变量是为了构建单位矩阵，目的达到后过河拆桥，让他们全部从基矩阵里出去吧)
如果辅助规划最优解人工变量不全为零，则原LP问题无可行解。

阶段2：划去辅助规划最优表中人工变量所在列，求解原规划

 

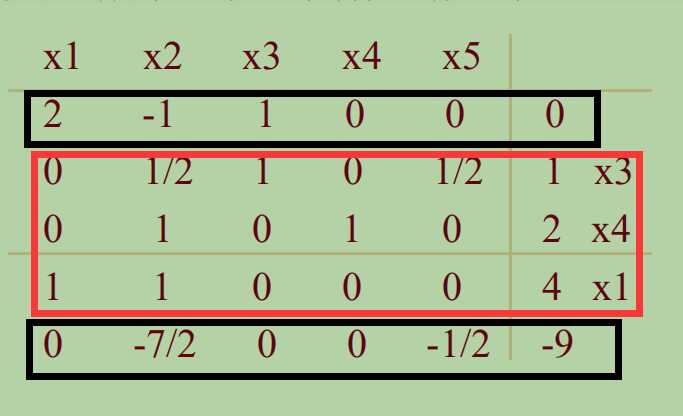
　　检验数显示目标函数值已不可能增加，max问题最优解找到，，最优目标值为