uoj#62 怎样跑的更快 （莫比乌斯反演）

Posted 2021-02-11 tuchen

题目链接：http://uoj.ac/problem/62

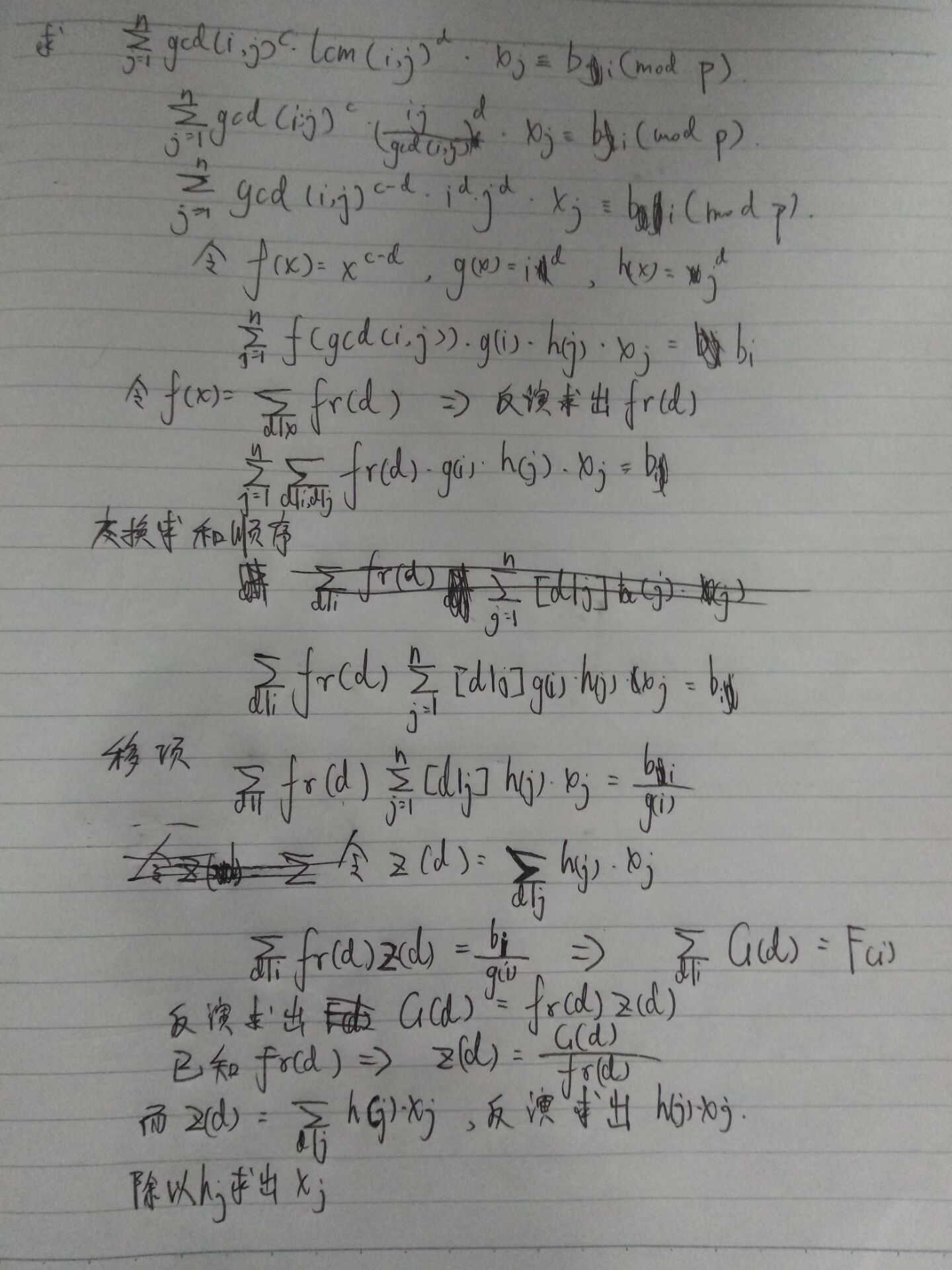
推式子呀推式子

发现我对莫比乌斯反演一无所知qaq

预处理出要用的数组，然后反演反演反演就好啦

 

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<stack>
#include<cmath>
using namespace std;
typedef long long ll;

const int maxn = 100010;
const int mod = 998244353,pmod=mod-1;

int n,c,d,q;
int b[maxn],f[maxn],fr[maxn],g[maxn],h[maxn],ans[maxn];

int qsm(int i,int po){
    int res=1;
    while(po){
        if(po&1) res=1ll*res*i%mod;
        i=1ll*i*i%mod;
        po>>=1;
    } return res;
}

int isp[maxn],prime[maxn],mu[maxn],tot;

void init(){
    isp[1],mu[1]=1;
    for(int i=2;i<=100000;++i){
        if(!isp[i]){
            prime[++tot]=i;
            mu[i]=-1;
        }
        for(int j=1;j<=tot&&i*prime[j]<=100000;++j){
            isp[i*prime[j]]=1;
            if(i%prime[j]!=0){
                mu[i*prime[j]]=-mu[i];
            }else{
                mu[i*prime[j]]=0;
                break;
            }
        }
    }
    int mi=((c-d)%pmod+pmod)%pmod; // 欧拉定理   处理指数为负 
    for(int i=1;i<=100000;++i) f[i]=qsm(i,mi);
    for(int i=1;i<=100000;++i){
        for(int j=1;i*j<=100000;++j){
            fr[i*j]=((fr[i*j]+1ll*mu[j]*f[i]%mod)%mod+mod)%mod;
        }
    }
    for(int i=1;i<=100000;++i) g[i]=qsm(i,d);
}

void solve(){
    memset(h,0,sizeof(h));
    memset(ans,0,sizeof(ans));
    
    for(int i=1;i<=n;++i) b[i]=1ll*b[i]*qsm(g[i],mod-2)%mod;
    
    for(int i=1;i<=n;++i){
        for(int j=1;i*j<=n;++j){
            h[i*j]=((h[i*j]+1ll*mu[j]*b[i]%mod)%mod+mod)%mod;
        }
    }
    
    for(int i=1;i<=n;++i){
        if(fr[i]==0&&h[i]!=0){ printf("-1
"); return; } // 非0数除0无解 
        h[i]=1ll*h[i]*qsm(fr[i],mod-2)%mod;
    }
    
    for(int i=1;i<=n;++i){
        for(int j=1;j*i<=n;++j){
            ans[i]=((ans[i]+1ll*mu[j]*h[i*j]%mod)%mod+mod)%mod;
        }
    }
    
    for(int i=1;i<=n;++i){
        if(ans[i]!=0&&g[i]==0){ printf("-1
"); return; }
        if(g[i]) ans[i]=1ll*ans[i]*qsm(g[i],mod-2)%mod; // 这里的特判注意一下 
        else ans[i]=0;
    }
    for(int i=1;i<=n;++i){
        printf("%d ",(ans[i]%mod+mod)%mod);
    }printf("
");
}

ll read(){ ll s=0,f=1; char ch=getchar(); while(ch<‘0‘ || ch>‘9‘){ if(ch==‘-‘) f=-1; ch=getchar(); } while(ch>=‘0‘ && ch<=‘9‘){ s=s*10+ch-‘0‘; ch=getchar(); } return s*f;}

int main(){
    n=read(),c=read(),d=read(),q=read();
    init();
    while(q--){
        for(int i=1;i<=n;++i) b[i]=read();
        solve();
    }
    return 0;
}