牛顿迭代法 Newton's Method
Posted dummyummy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了牛顿迭代法 Newton's Method相关的知识,希望对你有一定的参考价值。
牛顿迭代法是一个用来求高次方程解的利器!
首先,有一个引理:切线是曲线的线性逼近
于是我们想到用切线来逼近曲线的根
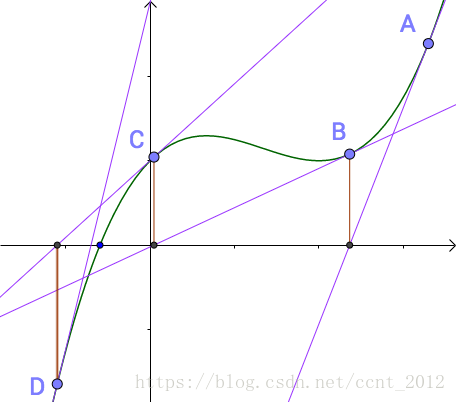
大概过程如下图所示:
(图片来自马同学高等数学的CSDN博客)
STEPS
1.先选择一个起始点(P_0(X_0,Y_0))
2.做出此处的切线,假设其与X轴交于(P_{0}^{'}(A0,B0))
3.做过(P_{0}^{'})X轴的垂线,交曲线于(P_1(X_1,Y_1))
4.将(P_1)作为新的起始点,并回到第一步
牛顿迭代法对要求的函数(f)有如下要求:
1.(f)二阶可导
2.起始点在根(x0)附近的某个区域中
但是对于(x^2-a=0),也就是开平方,随便选一个起始点就好啦,因为无论怎么选,牛顿迭代法对于它都是收敛的!
以上是关于牛顿迭代法 Newton's Method的主要内容,如果未能解决你的问题,请参考以下文章