语音信号的“短时时域”分析

Posted 2021-02-11 lxp-never

语音信号的预处理

语音信号的频带范围通常是300~3400Hz，一般情况下取采样率为8kHz，本博客的部分代码采用的是已经数字化了的语音。

预加重

　　预加重的目的是为了对语音的高频部分进行加重，去除口唇辐射的影响，增加语音的高频分辨率。

　　一般通过使用一阶FIR高通数字滤波器来实现预加重，滤波器函数为：

　　$$H(z)=1-alpha z^{-1}$$

　　其中$alpha $为预加重系数，$0.9<alpha<1.0$，

　　设n时刻的语音采样值为$x(n)$，经过预加重处理后的结果为$y(n)=x(n)-alpha x(n-1)$,这里$alpha=0.98$，

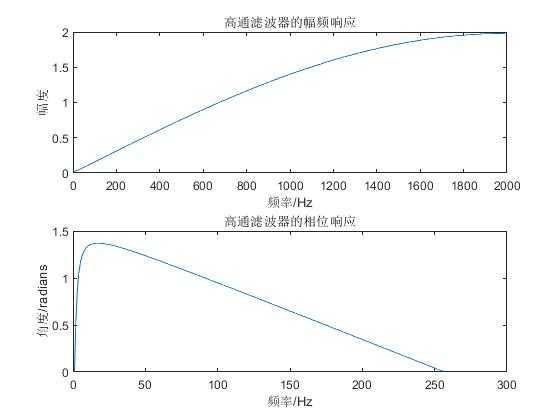
我们先来看看高通滤波器的幅频和相频响应：

clear;
[h1,f1]=freqz([1,-0.98],[1],256,4000);%高通滤波器
pha=angle(h1);           %高通滤波器的相位
H1=abs(h1);             %高通滤波器的幅值
figure(1);subplot(211);
plot(f1,H1);title(‘高通滤波器的幅频响应‘);
xlabel(‘频率/Hz‘);ylabel(‘幅度‘);
subplot(212);plot(pha);title(‘高通滤波器的相位响应‘);
xlabel(‘频率/Hz‘);ylabel(‘角度/radians‘);

View Code

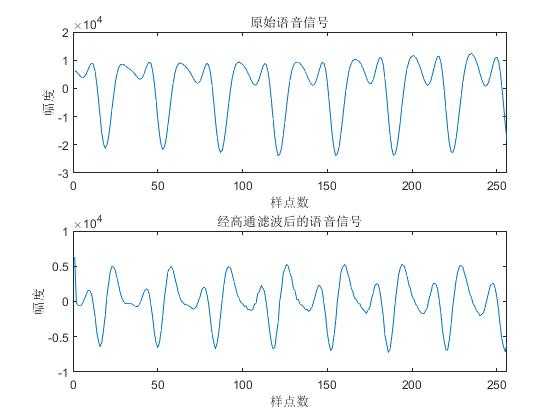
原始语音信号和经过滤波后的语音信号

fid=fopen(‘voice2.txt‘,‘rt‘);    %打开语音数字化文件
e=fscanf(fid,‘%f‘);          %读数据

ee=e(200:455);            %选取原始文件e的第200到455点的语音,也可选其他样点
figure(2);subplot(211);plot(ee);title(‘原始语音信号‘);
xlabel(‘样点数‘);ylabel(‘幅度‘);
axis([0 256 -3*10^4 2*10^4]);

r=fft(ee,1024);             %对信号ee进行1024点傅立叶变换
un=filter([1,-0.98],[1],ee);  %un为经过高频提升后的时域信号
subplot(212);plot(real(un));title(‘经高通滤波后的语音信号‘);
xlabel(‘样点数‘);ylabel(‘幅度‘);
axis([0 256 -1*10^4 1*10^4]);

View Code

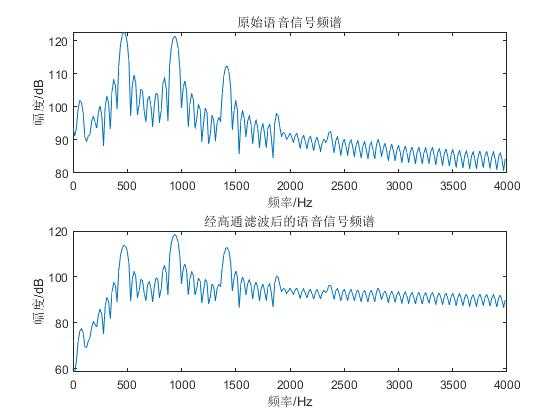
原始语音信号频率和经过滤波后的语音信号频率

clear;
fid=fopen(‘voice2.txt‘,‘rt‘);    %打开语音数字化文件
e=fscanf(fid,‘%f‘);          %读数据
ee=e(200:455);            %选取原始文件e的第200到455点的语音,也可选其他样点
r=fft(ee,1024);             %对信号ee进行1024点傅立叶变换
r1=abs(r);                 %对r取绝对值 r1表示频谱的幅度值
pinlv=(0:1:255)*8000/512;    %点和频率的对应关系
yuanlai=20*log10(r1);       %对幅值取对数
signal(1:256)=yuanlai(1:256);%取256个点，目的是画图的时候，维数一致
figure(1);subplot(211);plot(pinlv,signal);title(‘原始语音信号频谱‘);
xlabel(‘频率/Hz‘);ylabel(‘幅度/dB‘);

r2(1:256)=r(1:256);
[h1,f1]=freqz([1,-0.98],[1],256,4000);%高通滤波器
u=r2.*h1‘;               % 将信号频域与高通滤波器频域相乘 相当于在时域的卷积
u2=abs(u);              %取幅度绝对值
u3=20*log10(u2);        %对幅值取对数
subplot(212);plot(pinlv,u3);title(‘经高通滤波后的语音信号频谱‘);
xlabel(‘频率/Hz‘);
ylabel(‘幅度/dB‘);

View Code