堆排序
Posted jinliang374003909
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了堆排序相关的知识,希望对你有一定的参考价值。
前言:网上有很多堆排序的案例,我只想写自己堆排序。
一:堆结构
即:一个父节点最多只能有两个子节点(可以没有),如下图
图1 图2
图2 图3
图3  图4
图4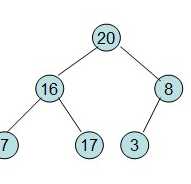
二: 数组与堆结构转换
假设已知堆数组 int[] a = {9,7,6,4,5,1,3,2,} 则相应对结构如下
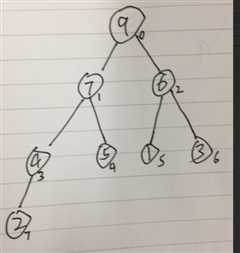
图5
备注: 一个父节点(pNode 为图5中的7 )和两个子节点(4(lNOde 左节点)和5(rNode 右节点))的关系
左节点: lNOde = 2*pNode + 1 ;
右节点 : rNode = 2*pNode +2 ;
三:通过已知数组建立成堆结构数组
假设已知数组 int[] a = { 7,9,6,4,5,1,3,2};
思路:对一个已知堆结构数组(长度为n)中添加一个元素,并调整该结果使之成为新的堆结构数组(长度变成 n+1)
步骤一:获取该数组的第一个元素 7 (a[0])为已知堆数组。
步骤二 :获取该数组的第下一个元素9(a[1])并添加到上一个堆结构数组中,并判断其的父节点是否大于自己,如果大于则交换父节点与自己的位置,交换后自己就在父节点的位置并把自己当成新的子节点,继续寻找父节点直至自己小于父节点并返回。如果大于则已是堆结构返回。以此类推直至成为新的堆结构。
步骤三 :重复步骤二,直至数组最后一个元素。
java实现:
/** * 建立堆模型 * * @param a */ private static void buildHeat(int[] a) { for (int i = 1; i < a.length; i++) { //注意我是从数组的第二个位置(即 index = 1)开始的 int parentNodeIndex = getParentNodeIndex(i); int currentIndex = i; while (parentNodeIndex >= 0) { // 判断子节点是否大于父节点 if (a[parentNodeIndex] < a[currentIndex]) { // 步骤2 自己大于父节点 交换父节点位置 // 父节点小于子节点 》》交换节点位置 int temp = a[parentNodeIndex]; a[parentNodeIndex] = a[currentIndex]; a[currentIndex] = temp; } else { // break; //步骤2 : 自己小于父节点结束循环(while)已成为新的堆结构。>>>>>>>执行步骤3 } currentIndex = parentNodeIndex; //步骤2 把自己当成新的子节点 parentNodeIndex = getParentNodeIndex(parentNodeIndex); } } }
四:去堆(获取排序)
步骤一:因为堆顶是整个堆结构中最大的数,所以我获取堆顶的哪个数9(a[0] 如图5),并把堆中最后一个数2(如图5)放入堆顶 (此时的数组长度是原来数组长度的减一)
步骤二 :调整堆结构(因为上一个步骤把 最后一个数放入如堆顶).。
调整方法: 获取获取左右子节点,先判断是否有子节点,然后判断两个子节点的大小(假设9已经换成了2,当前它有两个子节点,7(左子节点) 6 (右子节点)),获取到最大的子节点(7),并于父节点(2)比较 ,如果子节点大于父节点,交换父节点与子节点的位置,并把当前自己成为新的父节点重复调整方法,直至没有子节点或父节点大于所有子节点。成为新的堆结构
步骤三 :重复步骤一和二 ,直至没有改结构中没有子节点。
java实现
备注:代码与步骤二的调整方法有些不同 ,因为 1)如果没有左节点 (调整结束) 就一定不会有右节点?。2)如果有右节点就一定有左节点?。3)如果只有左节点没有右节点?
//去除堆 》》即排序 for(int j = 0; j < a.length; j++) { int lastIndex = a.length - 1 -j; int currentIndex = 0; int temp2 = a[0]; //步骤1 : 获取堆结构中的最大数 并与最后一个数交换位置 a[0] = a[lastIndex]; a[lastIndex] = temp2; while(true) { //获取左节点 int leftChildNodeIndex = getLeftChildNodeIndex(currentIndex); //步骤2 获取左节点位置 if(leftChildNodeIndex >= lastIndex) { //判断做节点是否有 有数 //没有左节点子节点 即去堆完成 for (int i = 0; i < a.length ; i++) { System.out.print(a[i] + ","); } System.out.println("没有左节点子节点 即去堆完成"); break; //步骤3 } //获取右节点 int rightChildNodeIndex = getRightChildNodeIndex(currentIndex); if(rightChildNodeIndex >= lastIndex) { //获取右节点 //没有右子节点 但有左节点 需要进行 交换 if (a[leftChildNodeIndex] > a[currentIndex]) { //判断左子节点 大于父节点 需要交换位置 int temp = a[leftChildNodeIndex]; a[leftChildNodeIndex] = a[currentIndex]; a[currentIndex] = temp; } for (int i = 0; i < a.length ; i++) { System.out.print(a[i] + ","); } System.out.println("没有右子节点 但有左节点"); break; //步骤3 } //即有左节点又有有节点 //先判断左右节点的大小 返回大节点 int whichIndexBig = a[leftChildNodeIndex] > a[rightChildNodeIndex] ? leftChildNodeIndex : rightChildNodeIndex; //判断子节点是否大于符节点 if (a[whichIndexBig] > a[currentIndex]) { //子节点大于父节点 需要交换子父节点的位置 int temp = a[whichIndexBig]; a[whichIndexBig] = a[currentIndex]; a[currentIndex] = temp; } //当前父节点 currentIndex = whichIndexBig; // } }
五 完整代码实现如下

package com.jinliang.sort; public class HeatSort { public static void main(String[] args) { int[] a = { 7,4,6,9,5,1,3,2}; //创建堆数组 buildHeat(a); for (int j = 0; j < a.length; j++) { System.out.print(a[j] + ","); } System.out.println("建队完成"); //int[] a = {42, 88, 77, 76, 66, 55, 64, 52, 45, 54, 34, 2, 32, 12, 35, 1, 22, 21, 34, 3}; //去除堆 》》即排序 for(int j = 0; j < a.length; j++) { int lastIndex = a.length - 1 -j; int currentIndex = 0; int temp2 = a[0]; a[0] = a[lastIndex]; a[lastIndex] = temp2; while(true) { //获取左节点 int leftChildNodeIndex = getLeftChildNodeIndex(currentIndex); if(leftChildNodeIndex >= lastIndex) { //没有左节点子节点 即去堆完成 for (int i = 0; i < a.length ; i++) { System.out.print(a[i] + ","); } System.out.println("没有左节点子节点 即去堆完成"); break; } //获取右节点 int rightChildNodeIndex = getRightChildNodeIndex(currentIndex); if(rightChildNodeIndex >= lastIndex) { //没有右子节点 但有左节点 需要进行 交换 if (a[leftChildNodeIndex] > a[currentIndex]) { //判断左子节点 大于父节点 需要交换位置 int temp = a[leftChildNodeIndex]; a[leftChildNodeIndex] = a[currentIndex]; a[currentIndex] = temp; } for (int i = 0; i < a.length ; i++) { System.out.print(a[i] + ","); } System.out.println("没有右子节点 但有左节点"); break; } //即有左节点又有有节点 //先判断左右节点的大小 返回大节点 int whichIndexBig = a[leftChildNodeIndex] > a[rightChildNodeIndex] ? leftChildNodeIndex : rightChildNodeIndex; //判断子节点是否大于符节点 if (a[whichIndexBig] > a[currentIndex]) { //子节点大于父节点 需要交换子父节点的位置 int temp = a[whichIndexBig]; a[whichIndexBig] = a[currentIndex]; a[currentIndex] = temp; } //当前父节点 currentIndex = whichIndexBig; } } //输出排序后的数组 for (int i = 0; i < a.length; i++) { System.err.print(a[i] + ","); } } /** * 建立堆模型 * * @param a */ private static void buildHeat(int[] a) { for (int i = 1; i < a.length; i++) { int parentNodeIndex = getParentNodeIndex(i); int currentIndex = i; while (parentNodeIndex >= 0) { // 判断子节点是否大于父节点 if (a[parentNodeIndex] < a[currentIndex]) { // 父节点小于子节点 》》交换节点位置 int temp = a[parentNodeIndex]; a[parentNodeIndex] = a[currentIndex]; a[currentIndex] = temp; } else { // break; } currentIndex = parentNodeIndex; parentNodeIndex = getParentNodeIndex(parentNodeIndex); } } } // 获取父节点索引 public static int getParentNodeIndex(int currentIndex) { int parentNodeIndex = (currentIndex - 1) % 2; Boolean isJO = (parentNodeIndex == 0) ? true : false; if (isJO) { // 奇数 // 获取父节点 return (currentIndex - 1) / 2; } parentNodeIndex = (currentIndex - 2) / 2; return parentNodeIndex; } // 获取left子节点索引 public static int getLeftChildNodeIndex(int currentIndex) { return 2 * currentIndex + 1; } // 获取right子节点索引 public static int getRightChildNodeIndex(int currentIndex) { return 2 * currentIndex + 2; } }
以上是关于堆排序的主要内容,如果未能解决你的问题,请参考以下文章
