[图解算法] 线性时间选择——//递归与分治策略//图解才是最直观

Posted 2021-02-11 cc1997

  1 #include <ctime> 
  2 #include <iostream>   
  3 using namespace std;   
  4   
  5 template <class Type>  
  6 void Swap(Type &x,Type &y);  
  7   
  8 inline int Random(int x, int y);  
  9   
 10 template <class Type>  
 11 void BubbleSort(Type a[],int p,int r);  
 12   
 13 template <class Type>  
 14 int Partition(Type a[],int p,int r,Type x);  
 15   
 16 template <class Type>  
 17 Type Select(Type a[],int p,int r,int k);  
 18   
 19 void main()  
 20 {  
 21     //初始化数组  
 22     int a[100];  
 23   
 24     //必须放在循环体外面  
 25     srand((unsigned)time(0));  
 26   
 27     for(int i=0; i<100; i++)  
 28     {  
 29         a[i] = Random(0,100);  
 30         cout<<"a["<<i<<"]:"<<a[i]<<" ";  
 31     }  
 32     cout<<endl; 
 33 
 34     cout<<"第23小元素是"<<Select(a,0,99,23)<<endl;  
 35   
 36 
 37     //重新排序，对比结果  
 38     BubbleSort(a,0,99);  
 39     for(i=0; i<100; i++)  
 40     {  
 41         cout<<"a["<<i<<"]:"<<a[i]<<" ";  
 42     }  
 43     cout<<endl;  
 44 }  
 45   
 46 template <class Type>  
 47 void Swap(Type &x,Type &y)  
 48 {  
 49     Type temp = x;  
 50     x = y;  
 51     y = temp;  
 52 }  
 53   
 54 inline int Random(int x, int y)  
 55 {  
 56      int ran_num = rand() % (y - x) + x;  
 57      return ran_num;  
 58 }  
 59   
 60 //冒泡排序  
 61 template <class Type>  
 62 void BubbleSort(Type a[],int p,int r)  
 63 {  
 64      //记录一次遍历中是否有元素的交换     
 65      bool exchange;    
 66      for(int i=p; i<r;i++)    
 67      {    
 68         exchange = false ;    
 69         for(int j=0; j<=r-i; j++)    
 70         {    
 71             if(a[j]<a[j-1])    
 72             {    
 73                 Swap(a[j],a[j-1]);   
 74                 exchange = true;    
 75             }     
 76         }     
 77         //如果这次遍历没有元素的交换,那么排序结束     
 78         if(false == exchange)    
 79         {  
 80              break ;    
 81         }  
 82      }  
 83 }  
 84   
 85 template <class Type>  
 86 int Partition(Type a[],int p,int r,Type x)  
 87 {  
 88     int i = p-1,j = r + 1;  
 89   
 90     while(true)  
 91     {  
 92         while(a[++i]<x && i<r);  
 93         while(a[--j]>x);  
 94         if(i>=j)  
 95         {  
 96             break;  
 97         }  
 98         Swap(a[i],a[j]);  
 99     }     
100     return j;  
101 }  
102   
103   
104 template <class Type>  
105 Type Select(Type a[],int p,int r,int k)  
106 {  
107     if(r-p<75)  
108     {  
109         BubbleSort(a,p,r);  
110         return a[p+k-1];  
111     }  
112     //(r-p-4)/5相当于n-5  
113     for(int i=0; i<=(r-p-4)/5; i++)  
114     {  
115         //将元素每5个分成一组，分别排序，并将该组中位数与a[p+i]交换位置  
116         //使所有中位数都排列在数组最左侧，以便进一步查找中位数的中位数  
117         BubbleSort(a,p+5*i,p+5*i+4);  
118         Swap(a[p+5*i+2],a[p+i]);  
119     }  
120     //找中位数的中位数  
121     Type x = Select(a,p,p+(r-p-4)/5,(r-p-4)/10);  
122     i = Partition(a,p,r,x);  
123     int j = i-p+1;  
124     if(k<=j)  
125     {  
126         return Select(a,p,i,k);  
127     }  
128     else  
129     {  
130         return Select(a,i+1,r,k-j);  
131     }  
132 }  

View Code

提醒：此篇需要先理解快速排序。

[图解+例子]

一、建立随机数组

 

（共27个数）（代码中为100个数，为了放得下举的例子改为27个）

---

 

 

二、给线性时间选择函数Select()传参

Type a[]  数组a

int p  起始位置

int r   结束位置

int k   查找第k小

---

 

 

三、判断

元素个数<75  不需要线性选择--》直接进行冒泡排序返回a[p+k-1](第k小元素)

元素个数>75   进行线性选择  --》进行下一步

---

 

 

四、线性时间选择

 

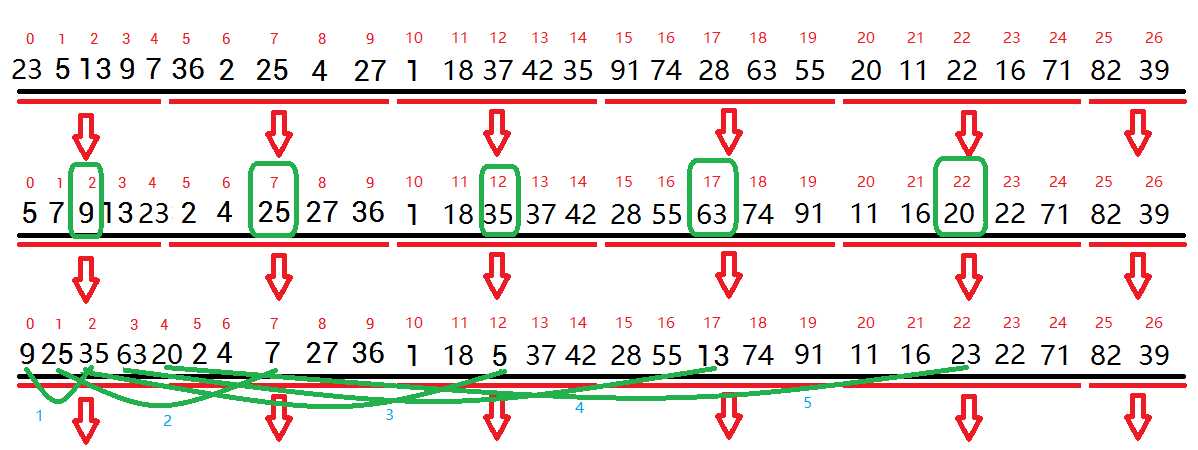
　　1- 分组并取各组中位数 （将元素每5个分成一组，分别排序，并将该组中位数与a[p+i]交换位置 ）【图中绿线12345表示要交换的一对对数据】

　　for(int i=0; i<=(r-p-4)/5; i++)
　　{
　　BubbleSort(a,p+5*i,p+5*i+4);
　　Swap(a[p+5*i+2],a[p+i]);
　　}

 
　　目的：使所有组的中位数都排列在数组最左侧，以便进一步查找中位数的中位数 

 

 

 

 

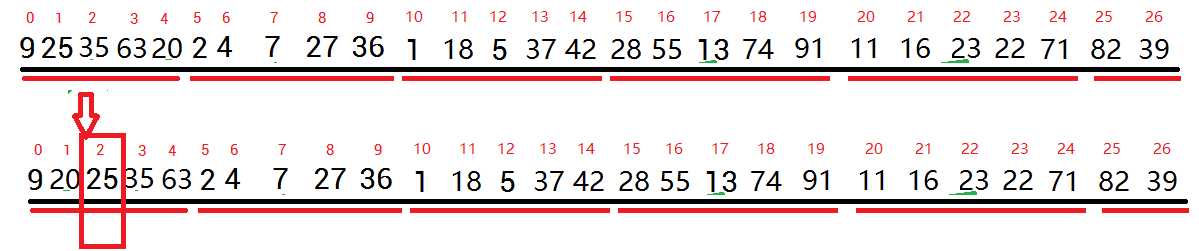
　　2- 查找中位数的中位数 

　　Type x = Select(a , p , p+(r-p-4)/5 , (r-p-4)/10 ); 

　　p到p+(r-p-4)/5为中位数的范围，p+(r-p-4)/5  ÷  2   =   (r-p-4)/10-->中位数的中位数

 ----------------------------------------------------------------------------------------------------------

　　

　　3-用找到的中位数的中位数做为快速排序的标准进行一趟快速排序（前面有篇讲的快速排序为了方便直接用第一个做标准，也有用随机数做标准的）

　　i = Partition(a,p,r,x);

　　排序结束后，标准元素将数组分为三部分：左，标准元素，右。

　　快排讲过啦，这里快速排序省略图解啦 ！想看点这里 快速排序

 ------------------------------------------------------------------------------------------------------------

　　4-判断　

　　快速排序后看成三部分：左，标准元素，右。

　　左都比标准元素小，右都比它大；（此时左右还是乱序，只有标准元素找到了它最终应该排的位置，这里不清晰先看快速排序那篇文章）

　　所以判断下我们要找的第k小是比它大（在右）还是比它小（在左）；

　　int j = i-p+1;
　　if(k<=j)
　　{
　　　　return Select(a,p,i,k);
　　}
　　else
　　{
　　　　return Select(a,i+1,r,k-j);
　　}

　　i为快速排序返回值，j = i - 起始位置 + 1;

　　小于或者等于，对左半段重复上述操作（递归）；

　　反之，对右半段。

  -----------------------------------------------------------------------------------------------------------------

[特例]

有空更新。。。

[总结]

线性时间选择其实就是————>>快速排序的加强版，

快速排序中的标准元素变为————>>分组后取得的各组中位数的中位数。

所以多了一步取中位数的操作而已。

 

本人保留解析著作权。

算法引用自 王晓东. 计算机算法设计与分析[M]. 电子工业出版社, 2012.