loj6436PKUSC2018神仙的游戏

Posted 2021-02-11 paul-guderian

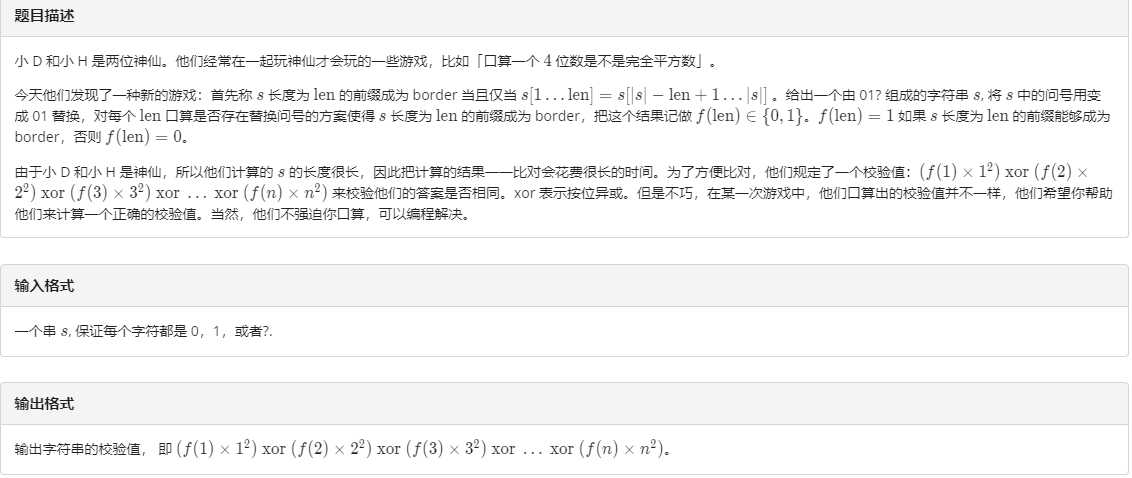
$|S| le 5 imes 10^5$

• 题解

  • 这题直接用通配符匹配的套路会错，因为重复部分的$?$可能同时被当做了$0$和$1$
  • 有长度为$i$的公共前缀后缀等价于有长度为$n-i$的循环节；
  • 对于循环节$d$，只需要知道对于任意的$d|i-j$，是否存在$(s[i]=‘0‘且s[j]=‘1‘) 或 (s[j]=‘0‘且s[i]=‘1‘)$
  • 构造函数：$A(x) = s[x]==‘0‘ , B(x) = s[n-1-x]==‘1‘ $
  • 可以通过计算多项式$A imes B$判断$d==i-j$的情况；
  • 所以枚举倍数$O(nlogn)$判断即可；
  • 时间复杂度：$O(|S|log|S|)$

 1 #include<bits/stdc++.h>
 2 #define ll long long 
 3 #define ld double
 4 using namespace std;
 5 const int N=2000010;
 6 const ld pi=acos(-1);
 7 struct C{
 8     ld x,y;
 9     C(ld _x=0,ld _y=0):x(_x),y(_y){};
10     C operator +(const C&a)const{return C(x+a.x,y+a.y);}
11     C operator -(const C&a)const{return C(x-a.x,y-a.y);}
12     C operator *(const C&a)const{return C(x*a.x-y*a.y,x*a.y+y*a.x);}
13     C operator /(const ld&a)const{return C(x/a,y/a);}
14 }a[N],b[N],c[N];
15 int n,t[N],L,rev[N],len;
16 char s[N];
17 void fft(C*a,int f){
18     for(int i=0;i<len;++i)if(i<rev[i])swap(a[i],a[rev[i]]);
19     for(int i=1;i<len;i<<=1){
20         C wn=C(cos(pi/i),f*sin(pi/i));
21         for(int j=0;j<len;j+=i<<1){
22             C w=C(1,0);
23             for(int k=0;k<i;++k,w=w*wn){
24                 C x=a[j+k],y=w*a[j+k+i];
25                 a[j+k]=x+y,a[j+k+i]=x-y;
26             }
27         }
28     }
29     if(!~f)for(int i=0;i<len;++i)a[i]=a[i]/len;
30 }
31 int main(){
32 //    freopen("bzoj5372.in","r",stdin);
33 //    freopen("bzoj5372.out","w",stdout);
34     scanf("%s",s);n=strlen(s);
35     for(int i=0;i<n;++i)a[i]=C(s[i]==‘0‘,0),b[i]=C(s[n-i-1]==‘1‘,0);
36     len=1;for(;len<n<<1;len<<=1,L++);
37     for(int i=1;i<len;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
38     fft(a,1);fft(b,1);
39     for(int i=0;i<len;++i)c[i]=a[i]*b[i];
40     fft(c,-1);
41     ll ans=1ll*n*n;
42     for(int i=1;i<n;++i){
43         ans^=1ll*(n-i)*(n-i);
44         for(int j=i;j<n;j+=i){
45             if((int)(c[n-j-1].x+0.1)||(int)(c[n+j-1].x+0.1)){
46                 ans^=1ll*(n-i)*(n-i);
47                 break;
48             }
49         }
50     }
51     cout<<ans<<endl;
52     
53     return 0;
54 }

View Code