18_2

Posted 2021-02-10 sybil-hxl

一、收获

1.层序输出二叉树，需要一个队列作为中转，如图（将就），以及queue模板的使用

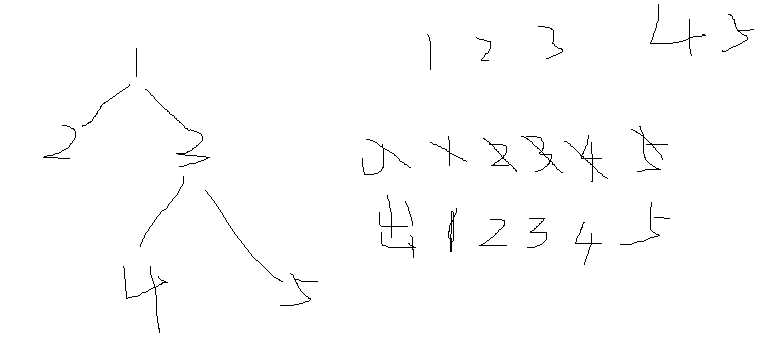
2.C++，当变量不好用时，可以考虑全局变量，虽然不太好，但是对于一个算法无妨

eg:

const int MAX=1000;
int arr[MAX][4]={0};
int n=0;
int dlmNum=1;//特别好用，如果不用全局，DLR中将无法编号
int coutData;//这个也很好用

 3.三叉树输入不是先序而是层序的问题：先用二维数组存储，再创建三叉树，学到了！！

4.当一个算法进行不下去的时候，一般来说，都是数据结构缺属性，大单添加就对了！

eg:

18_1添加了xd_num属性

struct XianDuan{
    int a_x;
    int a_y;
    int b_x;
    int b_y;
    int xd_num;//你的数据结构没有新线段中原始线段条数，缺乏一个合并的过程，怪不得没法处理
};

18_2添加了branch，dept，dlmrNum三个属性

struct Node{
    int data;
    Node *lchild,*mchild,*rchild;
    int branch;//0，分支数
    int dept;//1，深度
    int dlmrNum;//1，先序遍历顺序号
    Node(){
        branch=0;
        dept=1;
        dlmrNum=1;
    }
};

5.判断指针是否为空用 if(p) or if(!p)，见https://www.cnblogs.com/sybil-hxl/p/10427772.html

6.三叉树你真是个磨人的小妖精！都要把朕折磨死了！

二、题目

第二题

燕子会将巢穴建在最稳定的地方，对于三叉树而言 子分支越多，越稳定。

第一行输入n，之后输入n行，每行输入4个数字，分别为子节点，左孩子，中孩子，右孩子(确保每个根已经在之前出现过)，
计算子分支最多的节点中深度（高度）最深的节点编号(data)，如果深度相同按前序遍历顺序输出第一个

eg:
输入：
8
1 2 3 4
2 5 6 7
3 8 0 0
4 0 0 0
5 0 0 0
6 0 0 0
7 0 0 0
8 0 0 0

输出：
2

三、本题思路

1.创建三叉树

（1）由于输入不是先序，而是层序，先用二维数组存储，再创建三叉树

（2）创建时候

①找出当前节点所在的行index，判断条件是该行第一个元素==当前（父）节点的data值

②对当前行的3个孩子分别进行赋值，若不是叶子则创建新子节点

2.先序遍历，目的是得到先序排序的顺序号

3.层序遍历，目的是得到子分支数和深度（以及最后的排序）

4.排序：按照分支数（大）>深度（深）>先序遍历顺序号（小/先）排序所有节点

（1）对于非数组类型的树指针，没法用qsort/sort排序，只能自己写算法比较，写在LayerOrder的最后！

（2）若把树改为结构体数组就能用qsort/sort，重写cmp函数实现二级排序！（这个暂时还没写，用数组比指针相对安全吧）

四、代码

#include <iostream>
#include <stdlib.h>
#include <queue>
#include <algorithm>
using namespace std;
const int MAX=1000;
int arr[MAX][4]={0};
int n=0;
int dlmNum=1;
int coutData;

struct Node{
    int data;
    Node *lchild,*mchild,*rchild;
    int branch;//0，分支数
    int dept;//1，深度
    int dlmrNum;//1，先序遍历顺序号
    Node(){
        branch=0;
        dept=1;
        dlmrNum=1;
    }
};
typedef Node* Tree;

void CreateTree(Tree &T){//层序创建三叉树
    int i=0;
    //1.找出当前节点所在的行index,即i
    for(i=0;i<n;i++){//从第1行开始（index为0），因为第一行就是root节点，已经赋值了
        if(arr[i][0] == T->data){
            break;
        }
    }
    //2.对当前行的3个孩子分别进行赋值，若不是叶子则创建新子节点
    if(arr[i][1]!=0){
        Node* anode=new Node;
        T->lchild=anode;
        anode->data=arr[i][1];
        CreateTree(anode);
    }else{
        T->lchild=NULL;
    }
    if(arr[i][2]!=0){
        Node* anode=new Node;
        T->mchild=anode;
        anode->data=arr[i][2];
        CreateTree(anode);
    }else{
        T->mchild=NULL;
    }

    if(arr[i][3]!=0){
        Node* anode=new Node;
        T->rchild=anode;
        anode->data=arr[i][3];
        CreateTree(anode);
    }else{
        T->rchild=NULL;
    }
}

void DLMR(Tree &T){
    if(T){
        T->dlmrNum=dlmNum++;//这里的序号，使用了全局变量，才得以实现
        //cout<<T->data;
        //cout<<"；序号："<<T->dlmrNum<<endl;
        DLMR(T->lchild);
        DLMR(T->mchild);
        DLMR(T->rchild);
    }
}

void LayerOrder(Tree &T){
    //1.入根
    //2.出根，入左中右（若NULL则不入）
    //3.左（新根，循环2,直到队列空）
    queue<Tree> q;
    q.push(T);
    int maxBranch=0;
    int maxDept=1;
    int minDlmrNum=1;
    coutData=T->data;
    while(!q.empty()){
        Tree front=q.front();//获取队列头节点
        q.pop();//出队列
        //cout<<front->data<<"	";
        if(front->lchild){//指针非空，入队列
            front->branch+=1;//分支数+1
            front->lchild->dept=front->dept+1;
            q.push(front->lchild);
        }
        if(front->mchild){
            front->branch+=1;
            front->mchild->dept=front->dept+1;
            q.push(front->mchild);
        }
        if(front->rchild){
            front->branch+=1;
            front->rchild->dept=front->dept+1;
            q.push(front->rchild);
        }

        //以下为输出最大值，也就是比较/排序
        if(front->branch > maxBranch){
            maxBranch=front->branch;
            coutData=front->data;
        }else if(front->branch == maxBranch){
            if(front->dept > maxDept){
                maxDept=front->dept;
                coutData=front->data;
            }else if(front->dept == maxDept){
                if(front->dlmrNum < minDlmrNum){
                    minDlmrNum=front->dlmrNum;
                    coutData=front->data;
                }
            }
        }
        //cout<<"；分支"<<front->branch<<"；层"<<front->dept<<endl;
    }
    cout<<coutData<<endl;
}

int cmp(const void *a,const void *b){
    int result=(*(Tree)b).branch - (*(Tree)a).branch;
    if(result==0){
        result=(*(Tree)b).dept - (*(Tree)a).dept;
        if(result==0){
            result=(*(Tree)a).dlmrNum - (*(Tree)b).dlmrNum;
        }
    }
    return result;
}

void main(){
    freopen("G:/18_2.txt","r",stdin);
    //关于输入不是先序而是层序的问题：先用二维数组存储，再创建三叉树
    cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<4;j++){
            cin>>arr[i][j];    
        }
    }
    Tree root=new Node;
    root->data=arr[0][0];
    CreateTree(root);
    //先序遍历，目的是得到先序排序的顺序号
    DLMR(root);    
    //层序遍历，目的是得到子分支数和深度（以及最后的排序）
    LayerOrder(root);
    //最后一步排序，对于非数组类型的树指针，没法用qsort/sort排序，只能自己写算法比较，写在LayerOrder的最后！

    //若把树改为结构体数组就能用qsort/sort实现二级排序！
    /*Tree tree=new Node[n];
    root->data=arr[0][0];
    CreateTree(root);
    //先序遍历
    DLMR(root);    
    //层序遍历
    LayerOrder(root);
    qsort(root,n,sizeof(Node),cmp);
    delete[] tree;*/
}