树·二叉查找树ADT（二叉搜索树/排序树）

Posted 2021-02-10 dhcao

1、定义

　　对于每个节点X，它的左子树中所有的项的值小于X的值，右子树所有项的值大于X的值。

　　

                                                    

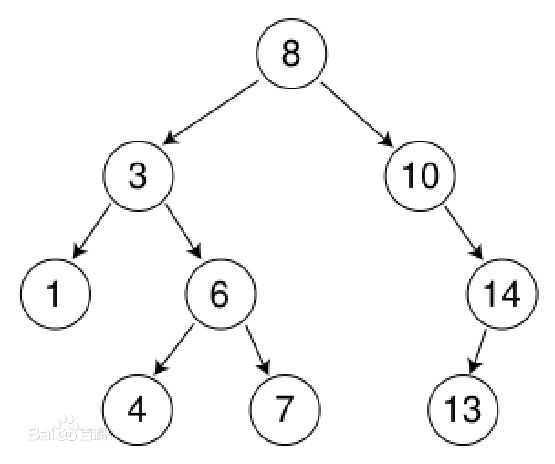
　　如图：任意一个节点，都满足定义，其左子树的所有值小于它，右子树的所有值大于它。

 

2、平均深度

　　在大O模型中，二叉查找树的平均深度是O(logN) 。

　　证明：查找某个节点x的算法深度，即从根出发找到节点x的路径长。所有查找的平均深度，就是平均内部路径长。

1. 假设二叉查找树共N个节点，假设左子树有i个节点，则右子树节点数目：N-i-1。
2. 假设D(N)表示具有N个基点的内部路径长。则N个节点的树的内部路径长：D(N) = D(i) + D(N-i-1) + N -1。（因为i为左子树，N-i-1 为右子树，所以其实际深度应该加上根节点的深度，所有每个节点都应该+1，除根外共有N-1个节点，所以最后要加上N-1）
3. j根i在求和中没有实际的区别，都是计数而已。

　　对D(N)进行i=(0,N-1)求和: (公式只能用word写出然后截图过来)

　　　                                                        　

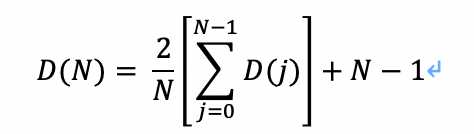
　　求解公式：得到　　

　　　　　　　　　　　　　　　　　　　　　　　

 

3、代码实现（递归）

　　二叉查找树完全代码：

　　3.1 ）根据查找树的性质，我们存放的值必定是可以比较的，所以我们选择 Comparable 作为eo对象的比较。

　　3.2）contains方法：是否含有x

　　　　如果存在节点的值为X，则返回true，否则返回false。

　　3.3）findMin和findMax方法：

　　　　二叉查找树的所有节点都有其顺序，这两个方法可以方便的找出最大最小值。

　　3.4）insert方法：插入x

　　　　插入操作：按照顺序查找，如果找到x，则直接返回树，否则在合适的地方插入x。

　　3.5）remove方法：移除x

　　　　删除操作：如果x是叶子节点，则直接删除，返回树，如果x含有左子树或者右子树，或者含有左右子树，则要做适当的调整树结构。

package chapterFour;

import java.nio.BufferUnderflowException;

/**
 * 二叉查找树：
 * 左子树的所有项的值均小于根节点，右子树的所有项的值均大于根节点。
 */
public class BinarySearchTree<T extends Comparable<? super T>> {


    /**
     * 节点类
     *
     * @param <T>
     */
    private static class BinaryNode<T> {

        private T element;
        private BinaryNode<T> left;
        private BinaryNode<T> right;

        BinaryNode(T t) {
            this(t, null, null);
        }

        public BinaryNode(T t, BinaryNode<T> lt, BinaryNode<T> rt) {
            element = t;
            left = lt;
            right = rt;
        }
    }

    // 根节点
    private BinaryNode<T> root;

    /**
     * 构造函数
     */
    public BinarySearchTree() {
        root = null;
    }

    /**
     * 清空整颗树
     */
    public void makeEmpty() {
        root = null;
    }

    /**
     * 判断树是否为空：只需要判断根节点是否为空即可。
     *
     * @return
     */
    public Boolean isEmpty() {
        return root == null;
    }

    /**
     * 是否含有节点x,含有则返回true，没有则返回fales
     *
     * @param x
     * @return
     */
    public boolean contains(T x) {
        return contains(x, root);
    }

    /**
     * 寻找最小值
     *
     * @return
     */
    public T findMin() {
        if (isEmpty()) {
            throw new BufferUnderflowException();
        }
        return findMin(root).element;
    }

    /**
     * 寻找最小值
     *
     * @return
     */
    public T findMax() {
        if (isEmpty()) {
            throw new BufferUnderflowException();
        }
        return findMax(root).element;
    }

    /**
     * 插入
     *
     * @param t
     */
    public void insert(T t) {
        root = insert(t, root);
    }

    /**
     * 删除
     *
     * @param t
     */
    public void remove(T t) {
        root = remove(t, root);
    }

    /**
     * 打印全部
     */
    public void printTree() {
        if (isEmpty()) {
            System.out.println("Empty tree");
        } else {
            printTree(root);
        }
    }


    /**
     * 删除方法：
     * 删除一个节点，如果是叶子节点，那么直接删除就好了，但是如果是某个父节点，那么需要重组部分树节点。
     *
     * @param t
     * @param root
     * @return
     */
    private BinaryNode<T> remove(T t, BinaryNode<T> root) {

        if (root == null) {
            return root;
        }

        int compareResult = t.compareTo(root.element);

        if (compareResult < 0) {
            root.left = remove(t, root.left);
        } else if (compareResult > 0) {
            root.right = remove(t, root.right);
        } else if (root.left != null && root.right != null) {
            root.element = findMin(root.right).element;
            root.right = remove(root.element, root.right);
        } else {

            root = (root.left != null) ? root.left : root.right;
        }
        return root;

    }

    /**
     * 查找树的插入，其实很简单，就一直的递归，然后插入就好了。
     *
     * @param t
     * @param root
     * @return
     */
    private BinaryNode<T> insert(T t, BinaryNode<T> root) {

        // 如果树不存在就创建一棵树
        if (root == null) {
            return new BinaryNode<>(t, null, null);
        }
        int compareResult = t.compareTo(root.element);

        // 如果比root小，就插入到root的左边
        if (compareResult < 0) {
            root.left = insert(t, root.left);
        }
        // 如果比root大，就插入到root的右边
        if (compareResult > 0) {
            root.right = insert(t, root.right);
        }
        // 最后返回树
        return root;

    }

    /**
     * 寻找最大值（方法一，用循环代替递归）
     * 我们不使用递归，加判断的递归，可以用while循环
     *
     * @param root
     * @return
     */
    private BinaryNode<T> findMax(BinaryNode<T> root) {

        if (root == null) {
            return null;
        }

        while (root.right != null) {
            root = root.right;
        }
        return root;
    }

    /**
     * 寻找最小值（方法二，直接使用递归）
     * 我们用递归的方法，遍历所有的左子树，直到最后。
     *
     * @param root
     * @return
     */
    private BinaryNode<T> findMin(BinaryNode<T> root) {
        if (root == null) {
            return null;
        }
        if (root.left == null) {
            return root;
        } else {
            return findMin(root.left);
        }
    }

    /**
     * 如果T是空集，那么可以就返回false。否则，存在T处的项是X，那么就可以返回ture，否则对树对左子树或右子树进行一次递归。
     *
     * @param x
     * @param root
     * @return
     */
    private boolean contains(T x, BinaryNode<T> root) {

        if (root == null) {
            return false;
        }

        // 判断x是在左子树还是右子树
        int compareResult = x.compareTo(root.element);

        if (compareResult < 0) {
            return contains(x, root.left);
        } else {
            return contains(x, root.right);
        }
    }

    /**
     * 按照顺序打印二叉树：中序遍历
     *
     * @param tb
     */
    private void printTree(BinaryNode<T> tb) {
        if (tb != null) {
            printTree(tb.left);
            System.out.println(tb.element);
            printTree(tb.right);
        }
    }

}