bzoj2989&&4170数列——二进制分组+主席树

Posted 2021-02-10 miracevin

题意的转化挺巧妙的

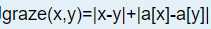
可以联想到曼哈顿距离！

并且，所谓的修改还要查询历史版本，并且修改之间不动只算一次，不就是给平面上加一个点吗？

看成(x,a[x])的点

就是一个菱形区域

转切比雪夫距离，变成矩形区域

所以

平面单点加，矩形查询和

1.cdq分治

2.树套树（离散化都不用）

3.二进制分组+主席树

这里，大炮打蚊子，用二进制分组来写

加入的点按操作二进制分组，每个组用主席树维护这个平面，查询在logn上查询，合并暴力重构，256MB又没有删除，所以重构完了把原来的树垃圾回收

注意：

主席树垃圾回收，从最后一个根开始，一个点不能删除两次，所以共用点打die标记，之后搜到返回即可。

代码：

写得很丑

其实不用vector，可以开数组，记录每个组的范围。每次sort，然后建树。

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^‘0‘)
#define mid ((l+r)>>1)
#define fi first
#define se second
#define mp(a,b) make_pair(a,b)
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=0;bool fl=false;
    while(!isdigit(ch=getchar()))(ch==‘-‘)&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=160000+5;
const int U=160000;
int n,q;
pair<int,int>a[N];
int b[N];
char ch[233];
struct node{
    int ls,rs;
    int sum;
    void clear(){
        ls=rs=sum=0;
    }
}t[40000*200];
int tot;
int sta[N],top;
int del[40000*200],dc;
bool die[40000*200];
int nc(){
    int r=dc?del[dc--]:++tot;
    die[r]=0;
    t[r].clear();
//    cout<<" r "<<r<<" "<<t[r].sum<<" "<<t[r].ls<<" "<<t[r].rs<<endl;
    return r;
    //return ++tot;
}
int cnt;
vector<pair<int,int> >mem[N];
vector<int>rt[N],pos[N];
bool cmp(pair<int,int>a,pair<int,int> b){//a<b?
    if(a.fi==b.fi) return a.se<b.se;
    return a.fi<b.fi;
}
void merge(int i,int j){
    vector<pair<int,int> >tmp;
    int l=0,r=0;
    for(reg k=1;k<=(int)mem[i].size()+(int)mem[j].size();++k){
        if(l>=(int)mem[i].size()){
            tmp.push_back(mem[j][r++]);
        }else if(r>=(int)mem[j].size()){
            tmp.push_back(mem[i][l++]);
        }else if(cmp(mem[i][l],mem[j][r])){
            tmp.push_back(mem[i][l++]);
        }else{
            tmp.push_back(mem[j][r++]);
        }
    }
    mem[i]=tmp;
}
void upda(int &x,int y,int l,int r,int p){
    if(!x) x=nc();
    t[x].sum=t[y].sum+1;
    if(l==r){return;}
    if(p<=mid){
        t[x].rs=t[y].rs;upda(t[x].ls,t[y].ls,l,mid,p);
    }else{
        t[x].ls=t[y].ls;upda(t[x].rs,t[y].rs,mid+1,r,p);
    }
}
void remove(int x){
    if(!x||die[x]) return;
    remove(t[x].ls);remove(t[x].rs);
    t[x].clear();
    die[x]=1;
    del[++dc]=x;
}
int query(int x,int y,int l,int r,int L,int R){
    //cout<<" query "<<x<<" "<<y<<" "<<l<<" "<<r<<" goal "<<L<<" "<<R<<endl;
    //cout<<" sum "<<t[x].sum<<"  and "<<t[y].sum<<endl;
    if(L<=l&&r<=R){
        return t[x].sum-t[y].sum;
    }
    int ret=0;
    if(L<=mid) ret+=query(t[x].ls,t[y].ls,l,mid,L,R);
    if(mid<R) ret+=query(t[x].rs,t[y].rs,mid+1,r,L,R);
    return ret;
}
void bing(int A,int B){
    //cout<<" merge "<<A<<" "<<B<<endl;
//    cout<<mem[A].size()<<" and "<<mem[B].size()<<endl;
    for(reg i=rt[A].size()-1;i>=0;--i)
        remove(rt[A][i]);
    for(reg i=rt[B].size()-1;i>=0;--i)
        remove(rt[B][i]);
//        cout<<" guibing "<<endl;
    merge(A,B);
    
    rt[A].clear();pos[A].clear();
    for(reg i=0;i<(int)mem[A].size();++i){
        if(i==0){
            rt[A].push_back(0);pos[A].push_back(mem[A][i].fi);
            upda(rt[A][0],0,-U,U,mem[A][i].se);
        }else{
            if(mem[A][i-1].fi==mem[A][i].fi){
                int tmp=rt[A][rt[A].size()-1];
                rt[A][rt[A].size()-1]=0;
                upda(rt[A][rt[A].size()-1],tmp,-U,U,mem[A][i].se);
            }else{
                rt[A].push_back(0);pos[A].push_back(mem[A][i].fi);
                upda(rt[A][rt[A].size()-1],rt[A][rt[A].size()-2],-U,U,mem[A][i].se);
            }
        }
    }
}
int calc(int x1,int y1,int x2,int y2){
    int ret=0;
    //cout<<" seventy-five "<<t[75].sum<<endl;
    for(reg i=1;i<=top;++i){
        int id=sta[i];
    //    cout<<" id "<<id<<" mem "<<mem[id].size()<<" pos "<<pos[id].size()<<endl;
    //    cout<<" seventy-five "<<t[75].sum<<endl;
        int k1=lower_bound(pos[id].begin(),pos[id].end(),y1)-pos[id].begin();
        --k1;
        int k2=upper_bound(pos[id].begin(),pos[id].end(),y2)-pos[id].begin();
        --k2;
    //    cout<<k1<<" and "<<k2<<endl;
    //    cout<<" seventy-five "<<t[75].sum<<endl;
        k1=k1<0?0:rt[id][k1];
        k2=k2<0?0:rt[id][k2];
        ret+=query(k2,k1,-U,U,x1,x2);
    //    cout<<" seventy-five "<<t[75].sum<<endl;
    }
    return ret;
}
int main(){
    rd(n);rd(q);
    int x;
    for(reg i=1;i<=n;++i){
        rd(x);a[i]=mp(i+x,i-x);
        b[i]=x;
    }
//    cout<<cmp(mp(3,-1),mp(6,-2))<<endl;
    sort(a+1,a+n+1,cmp);
    for(reg i=1;i<=n;++i){
        //cout<<"("<<a[i].se<<","<<a[i].fi<<")"<<endl;
        ++cnt;
        mem[cnt].push_back(a[i]);
        rt[cnt].push_back(0);
        pos[cnt].push_back(a[i].fi);
        upda(rt[cnt][0],0,-U,U,a[i].se);
        sta[++top]=cnt;
        while(top>1&&mem[sta[top]].size()==mem[sta[top-1]].size()){
            bing(sta[top-1],sta[top]);
            --top;
        }
    }
//    cout<<cnt<<" "<<top<<endl;
    int k;
    while(q--){
        scanf("%s",ch+1);
        rd(x);rd(k);
        if(ch[1]==‘Q‘){
        //    cout<<" seventy-five "<<t[75].sum<<endl;
            printf("%d
",calc(x-b[x]-k,x+b[x]-k,x-b[x]+k,x+b[x]+k));
        //    cout<<" seventy-five "<<t[75].sum<<endl;
        }else{
            ++cnt;
            mem[cnt].push_back(mp(x+k,x-k));
            rt[cnt].push_back(0);
            pos[cnt].push_back(x+k);
            upda(rt[cnt][0],0,-U,U,x-k);
            sta[++top]=cnt;
            while(top>1&&mem[sta[top]].size()==mem[sta[top-1]].size()){
                bing(sta[top-1],sta[top]);
                --top;
            }
            b[x]=k;
        ///    cout<<" seventy-five "<<t[75].sum<<endl;
        //    cout<<cnt<<" "<<top<<endl;
        }
    }
    return 0;
}

}
signed main(){
//    freopen("data.in","r",stdin);
//    freopen("my.out","w",stdout);
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
   Date: 2019/2/24 9:42:39
*/