线段树

Posted 2021-02-10 nvwang123

线段树

1、线段树是一棵二叉搜索树，它储存的是一个区间的信息。

2、每个节点以结构体的方式存储，结构体包含以下几个信息：

1.      区间左端点、右端点；（这两者必有）
2.      这个区间要维护的信息（事实际情况而定，数目不等）。

3、线段树的基本思想：        二分      。

4、线段树一般结构如图所示：

 

 

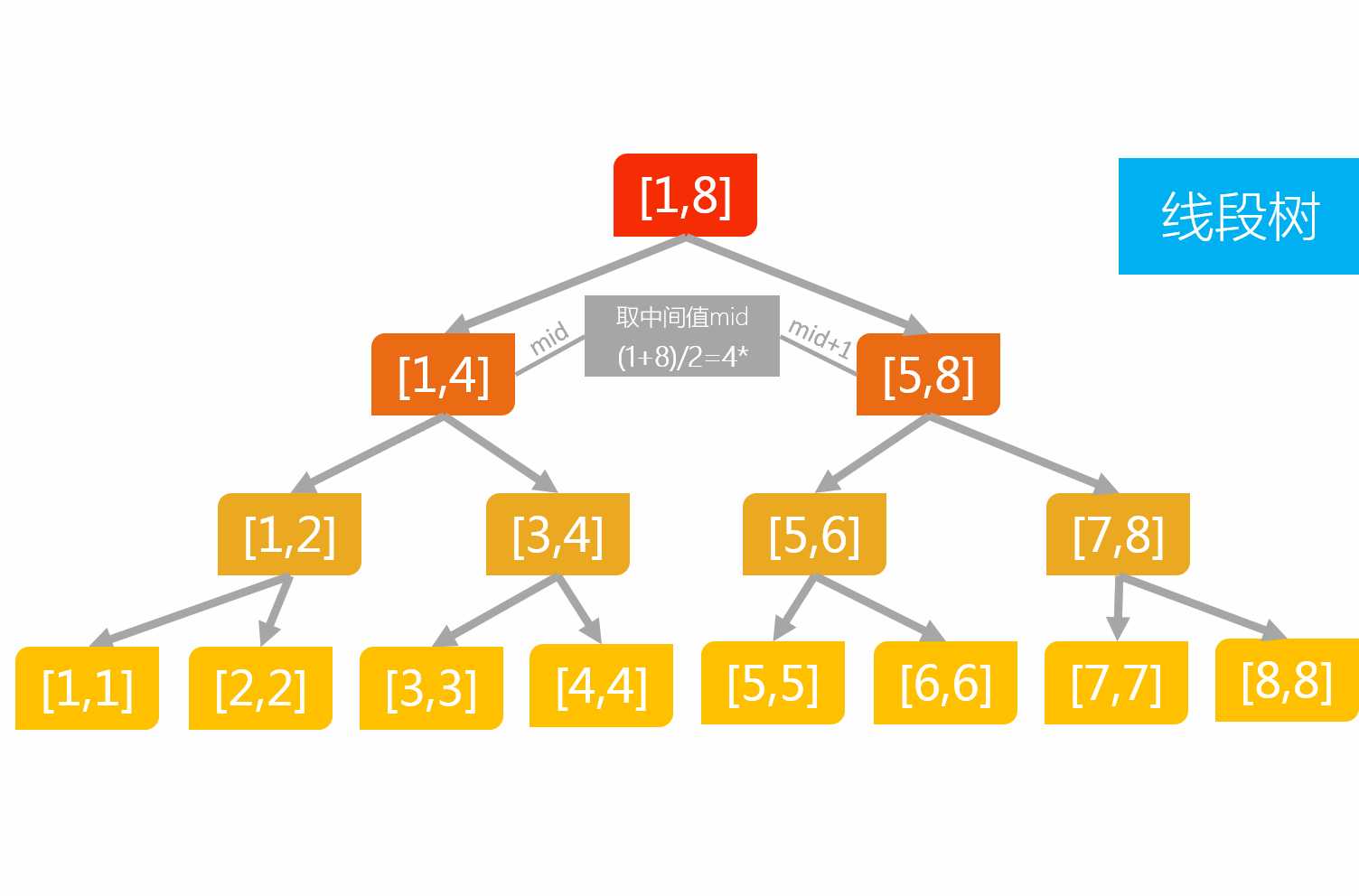
             每个节点的左孩子区间范围为[l，mid]，右孩子为[mid+1,r]

 

线段树的基础操作主要有5个：

             建树、单点查询、单点修改、区间查询、区间修改。

（以下均为求和操作）

 

 

 

1 struct node{
2     int l,r,w;//l左区间，r右区间，w区间和 
3 }xdtree[4*n];//n个数 

 

一、建树

a、对于二分到的每一个结点，给它的左右端点确定范围。

b、如果是叶子节点，存储要维护的信息。

c、状态合并。

！！：：      4倍空间

                    不要漏了return语句

 

 1 void build(int l,int r,int k){//k是根节点的下标
 2     
 3     xdtree[k].l=l;
 4     xdtree[k].r=r;
 5     
 6     if(l==r){
 7         
 8         cout<<xdtree[k].w;//n个数的和 
 9         return; 
10     }
11     
12     int m=(l+r)/2;
13     build(l,m,2*k);
14     build(m+1,r,2*k+1);
15     xdtree[k].w=xdtree[2*k].w+xdtree[2*k+1].w;
16     
17     } 

 

 

 

二、单点查询

 1 void ask(int k){//k一般为1，x是查询点
 2     int ans;
 3     
 4     if(xdtee[k].l==xdtree[k].r)
 5     ans=xdtree[k].w,return;
 6     
 7     int m=(xdtree[k].l + xdtree[k].r)/2;
 8     if(x<=m)  ask(k*2) ;//若目标靠左，递归左儿子 
 9     else ask(k*2+1);//目标靠右。递归右儿子 
10     
11 }

 

三、单点修改

第x个数加上y

 

 

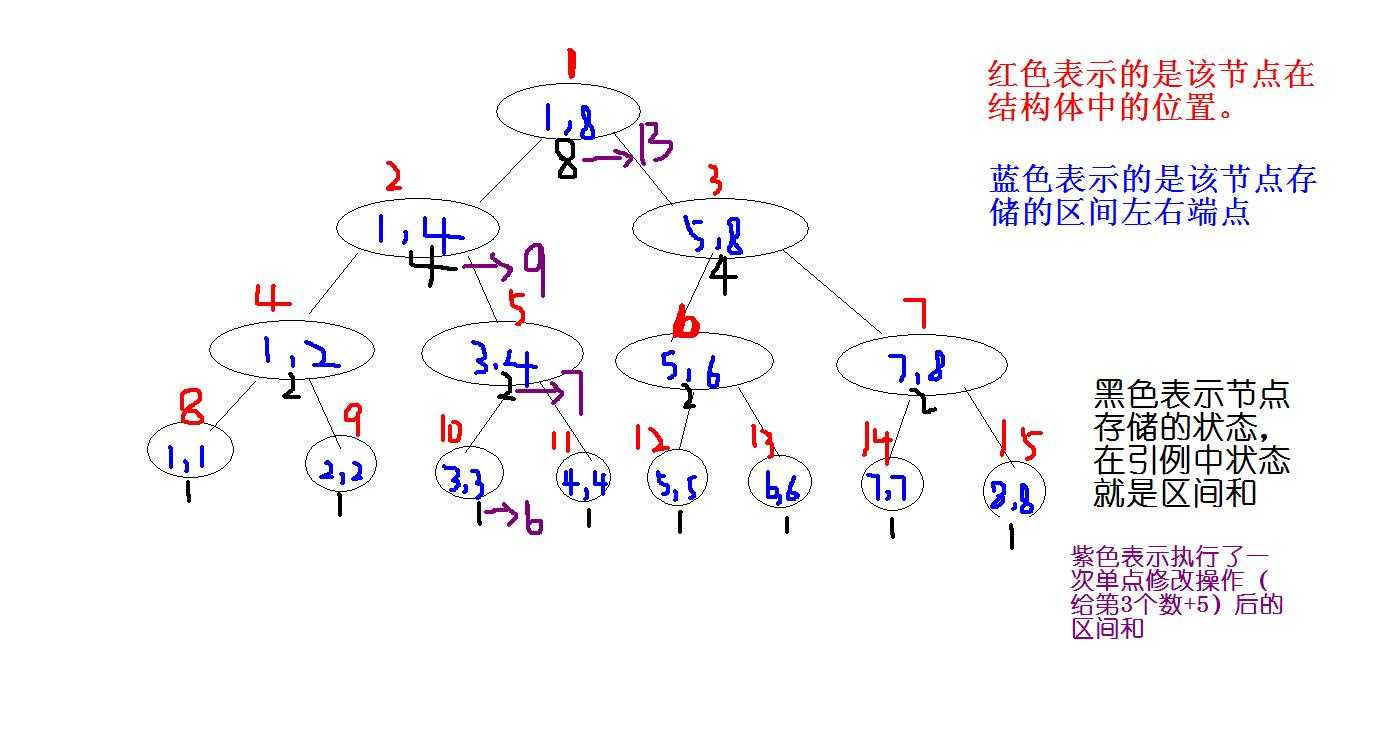
 1 void add(int k){
 2      
 3      if(xdtree[k].l==xdtree[k].r)
 4      xdtree[k].w+=y,return;
 5      
 6      int m=(xdtree[k].l+xdtree[k].r)/2;
 7      if(x<=m) add(k*2);
 8      else add(k*2+1);
 9      
10      xdtree[k].w=xdtree[k].w+xdtree[k].w;//更新包含k的节点 
11 } 
12  

 

四、区间查询

 

查询[ x , y ]的值

 

mid=(l+r)/2

x<=mid ,即 查询区间全在，当前区间的左子区间，往左孩子走

y>mid 即 查询区间全在，当前区间的右子区间，往右孩子走

否则，两个子区间都走

 

 1 void ask_(int k){
 2      
 3     if(xdtree[k].l>=x&&xdtree[k].r<=y)
 4     ans += xdtree[k].w,return;
 5     
 6     int m=(xdtree[k].l+xdtree[k].r)/2;
 7     
 8     if(x<=m) ask_(k*2);
 9     if(y>m)  ask_(k*2+1);
10     
11 } 
12  

 

 

 

#include<bits/stdc++.h>
using namespace std;
int n;
 
struct node{
    
    int l,r,w;//l左区间，r右区间，w区间和 
    
}xdtree[4*n];//n个数 

void build(int l,int r,int k){//k是根节点的下标 
    
    xdtree[k].l=l;
    xdtree[k].r=r;
    
    if(l==r){
        
        cout<<xdtree[k].w;//n个数的和 
        return; 
    }
    
    int m=(l+r)/2;
    build(l,m,2*k);
    build(m+1,r,2*k+1);
    xdtree[k].w=xdtree[2*k].w+xdtree[2*k+1].w;
    
    
} 


void ask(int k){//设x是查询点的下标 
    int ans=0;
    
    if(xdtee[k].l==xdtree[k].r)
    ans=xdtree[k].w,return;
    
    int m=(xdtree[k].l + xdtree[k].r)/2;
    if(x<=m)  ask(k*2) ;//若目标靠左，递归左儿子 
    else ask(k*2+1);//目标靠右。递归右儿子 
    
}

void add(int k){
     
     if(xdtree[k].l==xdtree[k].r)
     xdtree[k].w+=y,return;
     
     int m=(xdtree[k].l+xdtree[k].r)/2;
     if(x<=m) add(k*2);
     else add(k*2+1);
     
     xdtree[k].w=xdtree[k].w+xdtree[k].w;//更新包含k的节点 
} 

void ask_(int k){
     
    if(xdtree[k].l>=x&&xdtree[k].r<=y)
    ans += xdtree[k].w,return;
    
    int m=(xdtree[k].l+xdtree[k].r)/2;
    
    if(x<=m) ask_(k*2);
    if(y>m)  ask_(k*2+1);
    
} 
 
int main(){
    return 0;
}