算法进阶面试题03——构造数组的MaxTree最大子矩阵的大小2017京东环形烽火台问题介绍Morris遍历并实现前序/中序/后序

Posted 2021-02-10 xieyupeng

接着第二课的内容和带点第三课的内容。

 

（回顾）准备一个栈，从大到小排列，具体参考上一课....

 

 

 

构造数组的MaxTree

【题目】

定义二叉树如下：

public class Node{

    public int value;

    public Node left;

    public Node right;

 

    public Node(int data){

        this.value=data;

    }

}

一个数组的MaxTree定义如下：

◆ 数组必须没有重复元素

◆ MaxTree是一颗二叉树，数组的每一个值对应一个二叉树节点

◆ 包括MaxTree树在内且在其中的每一颗子树上，值最大的节点都是树的头。

给定一个没有重复元素arr，写出生成这个数组的MaxTree函数，要求如果数组长度为N，则时间复杂度为O(N)，额外空间复杂度为O(N)。

 

 

解法一：建出大根堆再重连成完全二叉树，o(n)

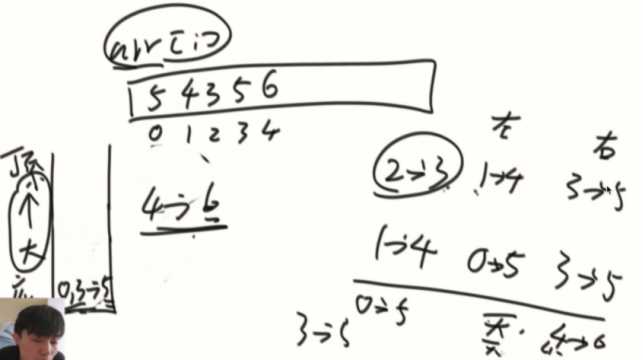
解法二：单调栈

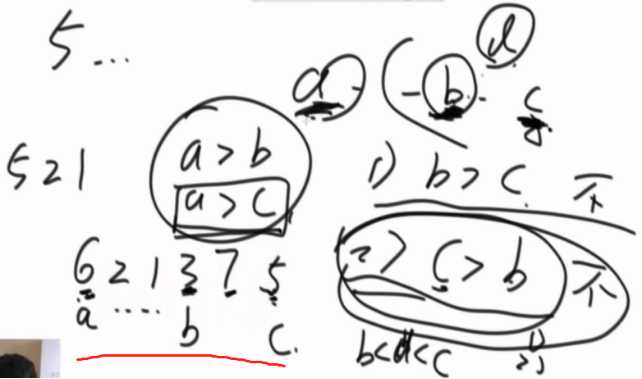
1、左右都没比他大的节点就是头节点

2、对于有左右其中一边的，这个数就串在有的底下，3在4底下

3、对于左右都有的，挂在左右中较小的数下，2在3底下

 

 

为什么可行？

为什么不会形成森林？

数组中没有重复值，最大值肯定是头节点，任何节点都串在比他大的，都有归属，最终以最大值为头部，所以是一棵树。

会不会出现一个节点多个孩子的情况？

首先先证明在任意一侧只有一棵树挂在他底下。

 

 

反证法：假设b、c都挂在a底下。

b>c的话，不可能c还会挂在a底下，存在矛盾。

c>b的话，b也不可能挂在a下，会挂在c底下。

 

老师版本（分开设置左右临近的最大值）

//构造数组的MaxTree
public class Code_02_MaxTree {

    //二叉树结点的定义如下
    public static class Node {
        public int value;
        public Node left;
        public Node right;

        //结点的初始化
        public Node(int data) {
            this.value = data;
        }
    }

    //构造数组的MaxTree函数
    public static Node getMaxTree(int[] arr) {
        Node[] nArr = new Node[arr.length];  //存放二叉树结点的数组
        for (int i = 0; i != arr.length; i++) {
            nArr[i] = new Node(arr[i]);
        }
        Stack<Node> stack = new Stack<Node>();//利用栈找出左右边第一个比自身大的数
        HashMap<Node, Node> lBigMap = new HashMap<Node, Node>();
        HashMap<Node, Node> rBigMap = new HashMap<Node, Node>();
        //从第一个开始
        // 找出所有数，左边第一个比自身大的数
        for (int i = 0; i != nArr.length; i++) {
            Node curNode = nArr[i];
            while ((!stack.isEmpty()) && stack.peek().value < curNode.value) {
                popStackSetMap(stack, lBigMap);//栈的一系列操作
            }
            stack.push(curNode);
        }
        while (!stack.isEmpty()) {
            popStackSetMap(stack, lBigMap);
        }
        //从最后一个开始
        // 找出所有数，右边第一个比自身大的数
        for (int i = nArr.length - 1; i != -1; i--) {
            Node curNode = nArr[i];
            while ((!stack.isEmpty()) && stack.peek().value < curNode.value) {
                popStackSetMap(stack, rBigMap);//栈的一系列操作
            }
            stack.push(curNode);
        }
        while (!stack.isEmpty()) {
            popStackSetMap(stack, rBigMap);
        }
        Node head = null; //声明头结点
        for (int i = 0; i != nArr.length; i++) {
            Node curNode = nArr[i];
            Node left = lBigMap.get(curNode);
            Node right = rBigMap.get(curNode);
            //左右都空，证明他是最大的头节点
            if (left == null && right == null) {
                head = curNode;
            } else if (left == null) {//左为空，就串在右的底下
                if (right.left == null) {//从左到右
                    right.left = curNode;
                } else {
                    right.right = curNode;
                }
            } else if (right == null) {//右为空，就串在左的底下
                if (left.left == null) {//从左到右
                    left.left = curNode;
                } else {
                    left.right = curNode;
                }
            } else {
                //选择左右较小的数为父节点
                Node parent = left.value < right.value ? left : right;
                if (parent.left == null) {//从左到右
                    parent.left = curNode;
                } else {
                    parent.right = curNode;
                }
            }
        }
        return head;
    }

    //栈的一系列操作
    public static void popStackSetMap(Stack<Node> stack, HashMap<Node, Node> map) {
        Node popNode = stack.pop();

        if (stack.isEmpty()) {
            map.put(popNode, null);
        } else {
            map.put(popNode, stack.peek()); //构造二叉树操作
        }

    }

    //二叉树的先序遍历
    public static void printPreOrder(Node head) {
        if (head == null) { return; }
        System.out.print(head.value + " ");
        printPreOrder(head.left);  //递归调用遍历二叉树
        printPreOrder(head.right);
    }

    //二叉树的中序遍历
    public static void printInOrder(Node head) {
        if (head == null) { return; }
        printInOrder(head.left);
        System.out.print(head.value + " ");
        printInOrder(head.right);
    }


    public static void main(String[] args) {
        int[] arr = {3, 4, 5, 1, 2};
        Node head = getMaxTree(arr);
        printPreOrder(head);
        System.out.println();
        printInOrder(head);
    }
}

 

自己码的版本（弹出一个数，同时设置其左右临近的最大值）

 

public class a03_01MaxTree {
    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }

    public static Node getMaxTree(int[] nodes) {
        Stack<Integer> stack = new Stack<Integer>();
        HashMap<Integer, Integer> lLarge = new HashMap<Integer, Integer>();
        HashMap<Integer, Integer> rLarge = new HashMap<Integer, Integer>();

        for (int i = 0; i != nodes.length; i++) {
            while (!stack.isEmpty() && nodes[i] > nodes[stack.peek()]) {
                int index = stack.pop();
                //谁让它弹出谁就是右边比他大的
                rLarge.put(index, i);
                //再通过栈来设置左边的情况
                if (stack.isEmpty()) {
                    lLarge.put(index, null);
                } else {
                    lLarge.put(index, stack.peek());
                }
            }
            stack.push(i);
        }
        //把栈里面剩下的元素处理下
        while (!stack.isEmpty()) {
            int index = stack.pop();
            rLarge.put(index, null);
            if (stack.isEmpty()) {
                lLarge.put(index, null);
            } else {
                lLarge.put(index, stack.peek());
            }
        }

        //形成Node数组
        Node[] treeNodes = new Node[nodes.length];
        for (int i = 0; i != nodes.length; i++) {
            treeNodes[i] = new Node(nodes[i]);
        }
        //建树
        Node head = null;
        for (int i = 0; i != nodes.length; i++) {
            Integer lLargeIndex = lLarge.get(i);
            Integer rLargeIndex = rLarge.get(i);
            if (lLargeIndex == null && rLargeIndex == null) {
                head = treeNodes[i];
            } else if (lLargeIndex == null) {
                if (treeNodes[rLargeIndex].left == null) {
                    treeNodes[rLargeIndex].left = treeNodes[i];
                } else {
                    treeNodes[rLargeIndex].right = treeNodes[i];
                }
            } else if (rLargeIndex == null) {
                if (treeNodes[lLargeIndex].left == null) {
                    treeNodes[lLargeIndex].left = treeNodes[i];
                } else {
                    treeNodes[lLargeIndex].right = treeNodes[i];
                }
            } else {//对比左右大小
                Node parent = nodes[lLargeIndex] > nodes[rLargeIndex] ? treeNodes[rLargeIndex] : treeNodes[lLargeIndex];
                if (parent.left == null) {
                    parent.left = treeNodes[i];
                } else {
                    parent.right = treeNodes[i];
                }
            }
        }
        return head;
    }

    //二叉树的先序遍历
    public static void printPreOrder(Node head) {
        if (head == null) { return; }
        System.out.print(head.value + " ");
        printPreOrder(head.left);  //递归调用遍历二叉树
        printPreOrder(head.right);
    }

    //二叉树的中序遍历
    public static void printInOrder(Node head) {
        if (head == null) { return; }
        printInOrder(head.left);
        System.out.print(head.value + " ");
        printInOrder(head.right);
    }


    public static void main(String[] args) {
        int[] arr = {3, 4, 5, 1, 2};
        Node head = getMaxTree(arr);
        printPreOrder(head);
        System.out.println();
        printInOrder(head);
    }

}

 

 

最大子矩阵的大小

　　给定一个整型矩阵map，其中的值只有0,1两种，求其中全是1 的所有矩阵区域中，最大的矩形区域为1的数量。

例如：

　　1  1  1  0

其中最大的矩形区域有3个1，所以返回3

例如：

　　1  0  1  1

      1  1  1  1

　　1  1  1  0

其中，最大的矩形区域有6个1，所以返回6

 

跳出这道题目，为了解决这个问题的一个引子题。

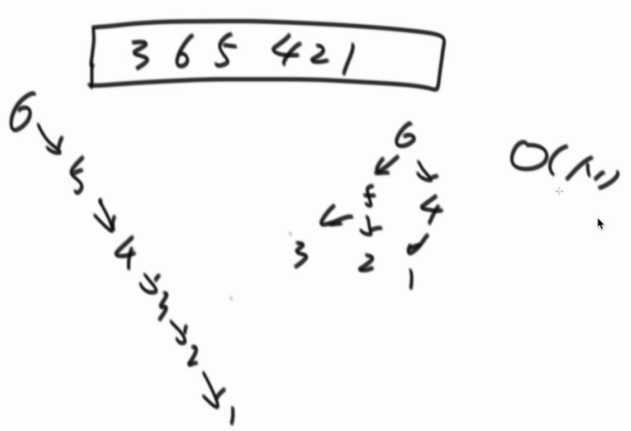
直方图找最大矩形

 

 

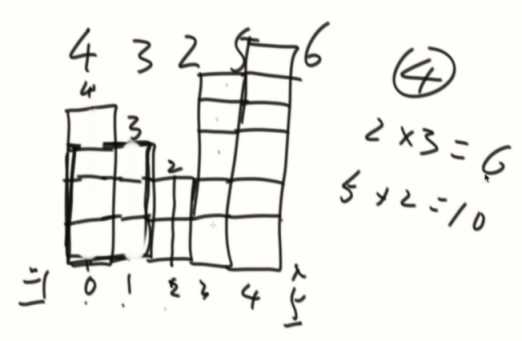
每个数都代表一个矩形，从第一个数开始尝试左右移动，碰到小的就停，例如4，面积就是4、3面积就是6....依次肯定会计算出最大的矩形。

利用单调栈，找到最近比他小的元素，弹出的时候，就可以计算出面积。

 

 

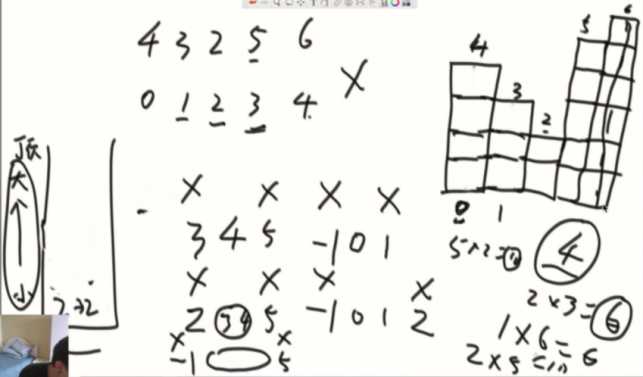
如果不是因为碰到比自己小的，全部元素过后，栈剩下的，就证明他们都能到达右边界（扩到5停）。

相等的情况：

 

 

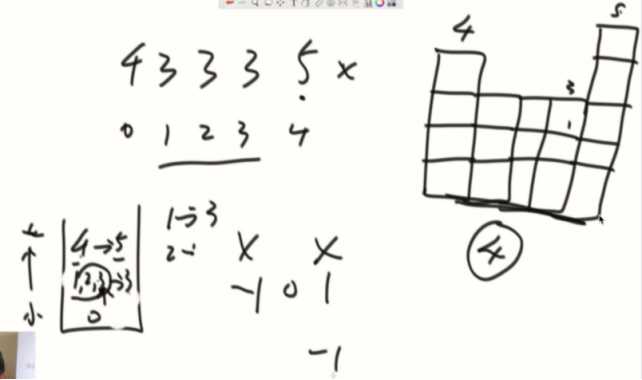
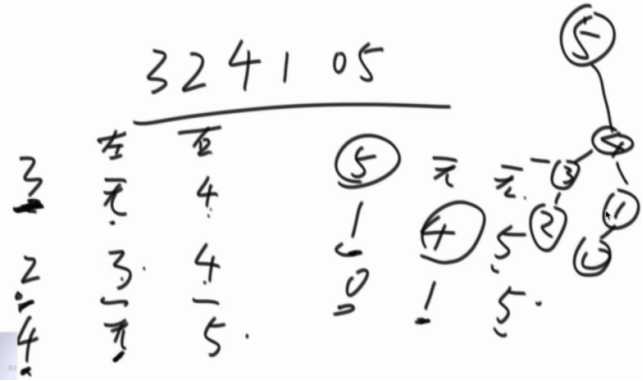
原始问题，完全借用了直方图的结论。

先看必须由第0行作为底，所有矩形中，哪个含有1是最多的。

接着看由第1行为底，每个位置，上面有多少个连续的1，然后通过这个计算结果，计算出哪个位置含1最多。

本次为0必为0，否则是之前的数再+1

 

 

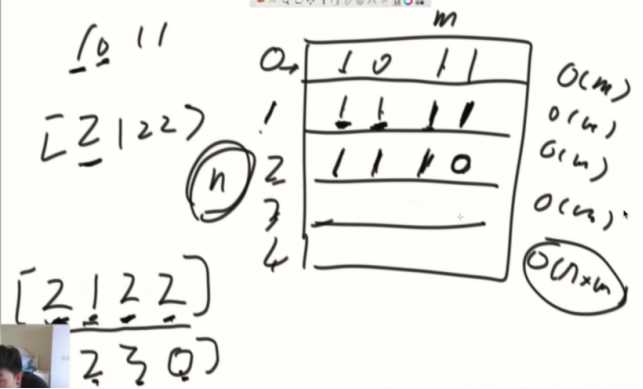
依次计算....

矩阵遍历一遍，o(n*m)搞定

代码解说：

public class Code_04_MaximalRectangle {

    //height数组表示在以当前行作为底的情况下，每个位置往上的连续的 1 的数量
    public static int maxRecSize(int[][] map) {
        if (map == null || map.length == 0 || map[0].length == 0) {
            return 0;
        }
        int maxArea = 0;
        //辅助数组
        int[] height = new int[map[0].length];
        for (int i = 0; i < map.length; i++) {
            for (int j = 0; j < map[0].length; j++) {
                height[j] = map[i][j] == 0 ? 0 : height[j] + 1;
            }
            maxArea = Math.max(maxRecFromBottom(height), maxArea);
        }
        return maxArea;
    }

    //找到柱子左边刚比它小的柱子位置，以及右边刚比它大的柱子位置，用栈计算最快
    //最基本的方法，如果一个数组表示直方图的话，在其中找到最大正方形
    //例如：[4,3,2,5,6]代表一个直方图
    private static int maxRecFromBottom(int[] height) {
        if (height == null || height.length == 0) {
            return 0;
        }
        int maxArea = 0;
        Stack<Integer> stack = new Stack<Integer>();
        //遍历数组中的每一个数
        for (int i = 0; i < height.length; i++) {
            //不断循环，直到当前位置的值小于栈顶元素
            while (!stack.isEmpty() && height[i] <= height[stack.peek()]) {
                int j = stack.pop();//值
                int k = stack.isEmpty() ? -1 : stack.peek();//左边界
                int curArea = (i - k - 1) * height[j];
                maxArea = Math.max(curArea, maxArea);
            }
            stack.push(i);
        }

        // 针对的是从栈底到栈顶一直递增的情况
        //结算栈中剩下的东西
        while (!stack.isEmpty()) {
            int j = stack.pop();//值
            int k = stack.isEmpty() ? -1 : stack.peek();//左边界
            int curArea = (height.length - k - 1) * height[j];
            maxArea = Math.max(curArea, maxArea);
        }
        return maxArea;
    }

    public static void main(String[] args) {
        int[][] num = new int[][]{
                {0,1,0,0,0,0},
                {1,1,1,1,1,1},
                {1,1,1,1,1,1},
                {1,1,1,1,1,1},
                {1,1,1,1,1,1}
        };
        System.out.println(maxRecSize(num));
    }

}

 

 

2017年京东原题：烽火台

给一个数组，代表环形的山

1、每座山上会放烽火，相邻可看见烽火

2、不相邻的山峰，两条路中其中一条路上的烽火都不大于他们之间的最小值，就能看见

返回能相互看见的山峰有多少对？

 

 

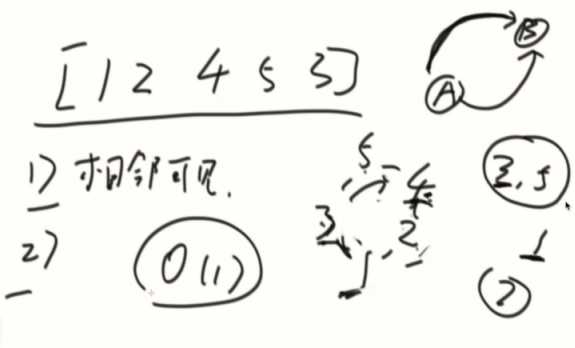
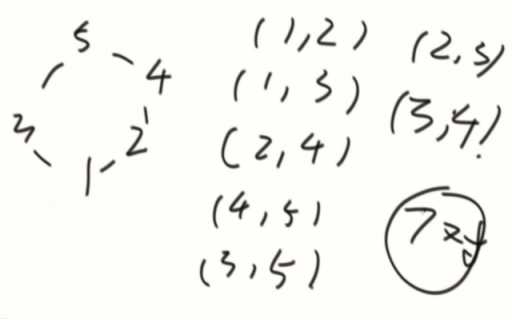
简单问法：数组值都不一样，o(1)。

 

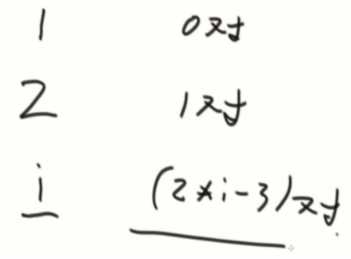
2*i-3对

证明：

把找法规定为：永远是小去找大。

3个数以及上，找到最高和次高，假设中间有一个值i，从i出发找大的，左边找到比i大的X停，右边找到Y停，就是两对。（最高和次高之间的每个数都能找到两个山峰对）

 

 

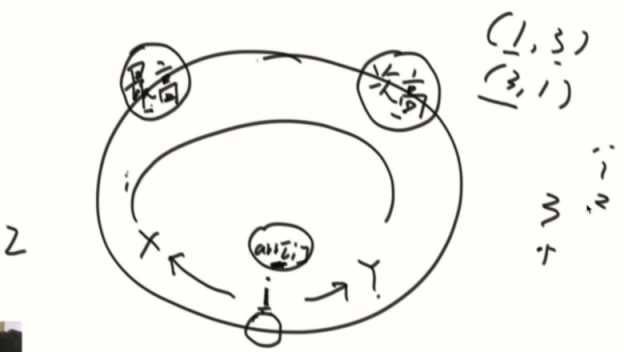
所以就是（(n-(最高+次高))*2）+1(最高和次高那条)

((n-2)*2)+1 = 2n-4+1 = 2n-3条

 

有重复值的情况：单调栈

找到第一个最大值，开始往后遍历

加入碰到4，入栈，碰到5，开始出栈，因为底部是5,1（代表5出现了1次），所以对于4来说找到两对可以看见的山峰。接着底部5+1，变成5,2。

 

 

大体思路还是小的找大的。（换成4也同理）

 

 

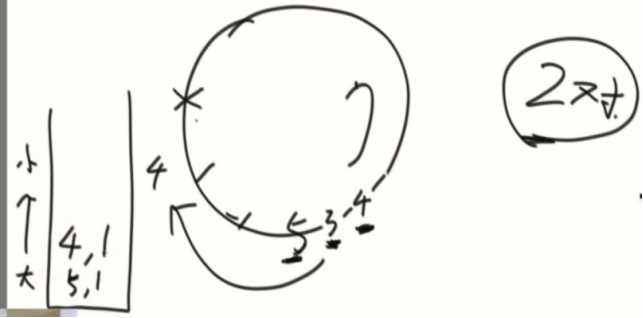
如果连续都是4，直到4,4碰上5，会产生两种互相看见的情况。

1、4和4之前相互看见，任意两个4都能相互看见，C₄²+4*2。

2、每个4左右边都能看见5，4*2。

 

 

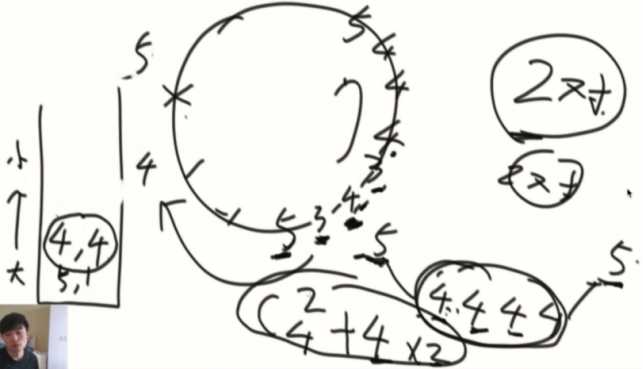
用最大值打底的原因：在结算的过程中因为有这个最大值的出现，可以确定这个数的顺时针方向可以找到比他大的。

 

最后栈里面还有东西，需要结算。

 

 

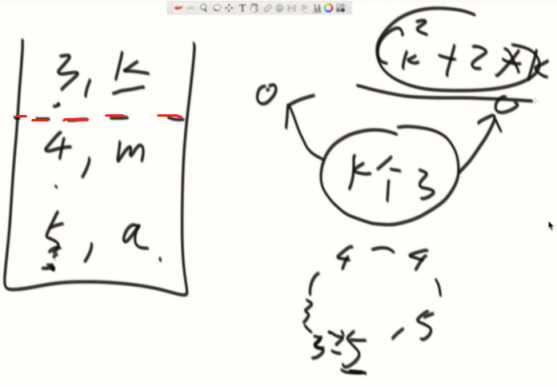
三条及以上的还是用那个通式

 

如果底下是2以上，依旧是通式

 

 

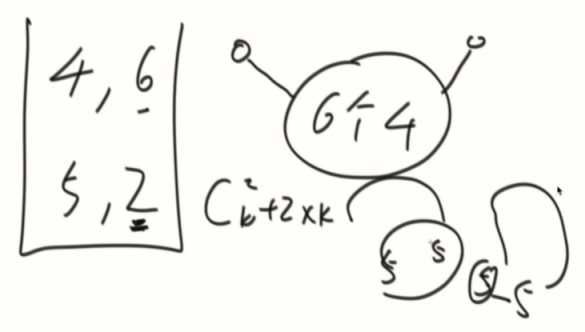
如果底下只有1个5（两边遇到最大的是同一个5），计算变成：

 

 

 

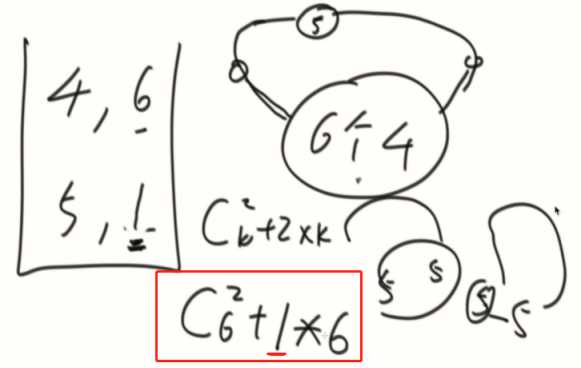
所以，倒数第二的数要考虑，最大值的数量

最后一个数，比一大就是单纯的C_k²，如果只有一个就是0对。

 

public class Code_05_MountainsAndFlame {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        while (in.hasNextInt()) {
            int size = in.nextInt();
            int[] arr = new int[size];
            for (int i = 0; i < size; i++) {
                arr[i] = in.nextInt();
            }
            System.out.println(communications(arr));
        }
        in.close();
    }

    public static class Pair {
        public int value;
        public int times;

        public Pair(int v) {
            this.value = v;
            this.times = 1;
        }
    }

    private static long communications(int[] arr) {
        if (arr == null || arr.length < 2) {
            return 0;
        }
        int size = arr.length;
        int maxIndex = 0;
        for (int i = 0; i < size; i++) {//获得最大值的下标
            maxIndex = arr[maxIndex] < arr[i] ? i : maxIndex;
        }
        int value = arr[maxIndex];//最大值
        int index = nextIndex(size, maxIndex);//最大值位置的下一个
        long res = 0L;//能互相看见的山峰数
        Stack<Pair> stack = new Stack<Pair>();
        stack.push(new Pair(value));//以最大值为底
        while (index != maxIndex) {//转一圈
            value = arr[index];
            while (!stack.isEmpty() && stack.peek().value < value) {
                int times = stack.pop().times;
//                res += getInternalSum(times) + times;
//                res += stack.isEmpty() ? 0 : times;
                res += getInternalSum(times) + 2 * times;
            }
            if (!stack.isEmpty() && stack.peek().value == value) {
                stack.peek().times++;//相等的话累加
            } else {
                stack.push(new Pair(value));
            }
            index = nextIndex(size, index);
        }
        //跑完一圈后，结算栈里面剩下的
        while (!stack.isEmpty()) {
            int times = stack.pop().times;
            //不管什么，肯定会内部产生山峰对
            res += getInternalSum(times);
            if (!stack.isEmpty()) {//没到最后一个
                res += times;
                if (stack.size() > 1) {//3个及以上的情况
                    res += times;
                } else {//第2个的情况，要结合最后一个数来判断
                    res += stack.peek().times > 1 ? times : 0;
                }
            }
        }
        return res;
    }

    //简单Ck(下标)2(上标)
    private static long getInternalSum(int n) {
        return n == 1L ? 0L : (long) n * (long) (n - 1) / 2L;
    }

    private static int nextIndex(int size, int i) {
        return i < (size - 1) ? (i + 1) : 0;
    }
}

 

做这些就是为了进自己想进的任何公司，加油！

笔试分数会决定是否签合同，按部门挑人。

 

开始第三课的内容

 

1、介绍一种时间复杂度O(N)，额外空间复杂度O(1)的二叉树的遍历方式，N为二叉树的节点个数

经典二叉树，无论递归还是非递归都逃不过，o(h)的额外空间复杂度，h为高度。

 

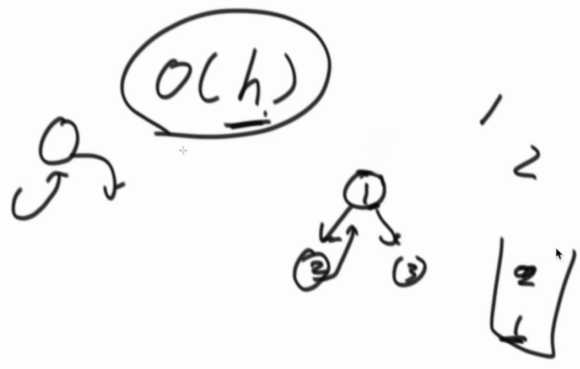
2、Morris遍历

利用Morris遍历实现二叉树的先序，中序，后序遍历，时间复杂度O(N)，额外空间复杂度O(1)。

利用了底层空闲的空间，在学术上称为线索二叉树

 

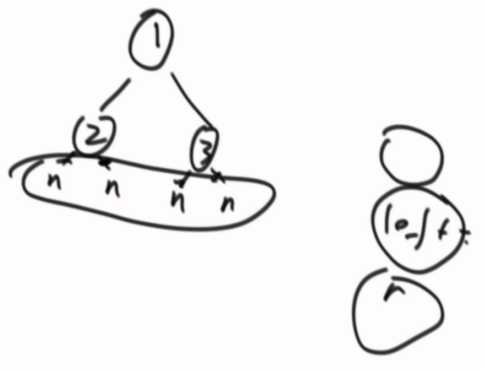
Morris遍历过程中的标准：

 

②...指向cur，让其指向空，cur向右移动

 

首先先忘掉什么前序中序后序遍历，这就叫Morris序

按标准走完全部流程。

 

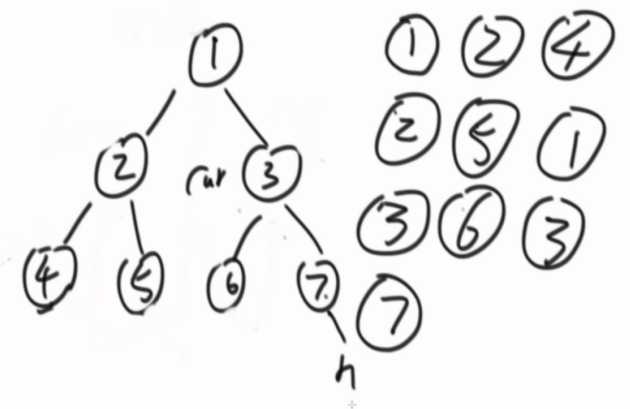
看一下本质：

只要这个节点有左子树，就能回到这个节点两次，如果没有左子树，只到达这个节点一次。

当第二次来到这个节点的时候，左子树的节点一定全部遍历完。

 

 

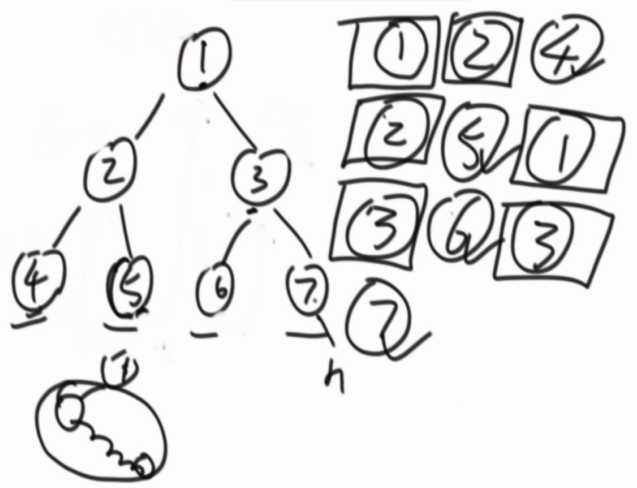
使用最右节点的右指针来标记，是第一次来到节点还是第二次来到。

不是完全二叉树也可以。

 

 

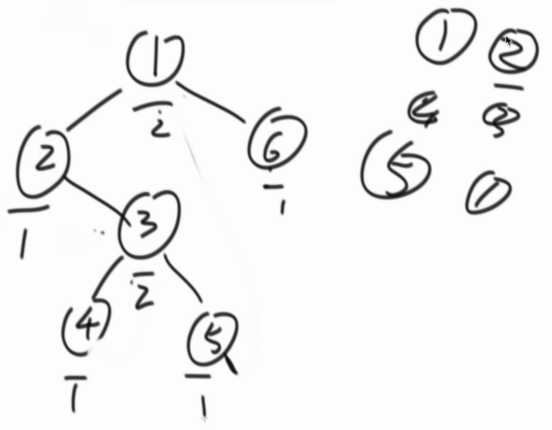
递归版本的遍历，会经过节点三次，打印时机在第一次就是先序，第二次中序，第三次后序。（最本质的是下面的遍历）

 

 

 

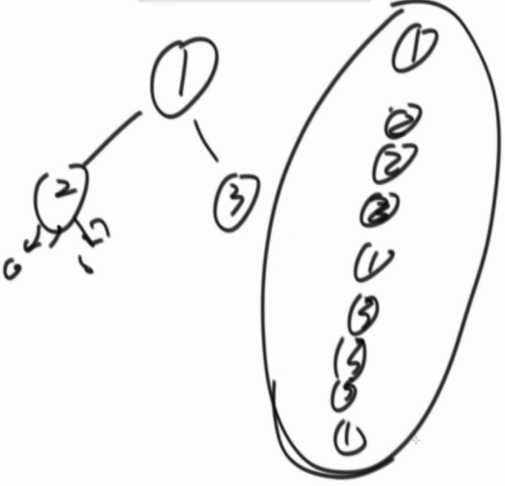
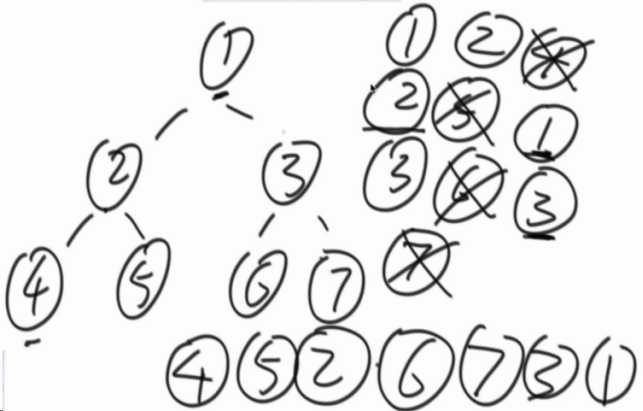
Morris，把第一次来到节点的时候打印，就是先序遍历。

打印时机放在最后一次来到这个节点的时候，就是中序遍历，例如一个节点有左子树，先把左子树处理完再打印，就是中序，当没有左子树的时候就直接打印（第一次和第二次重叠）。

 

怎么做到后序？

后序遍历只关心能到自己两次的节点，第二次到达节点的时候逆序打印左子树的右边界，打印完成后，在整个函数退出前，单独打印整课树的右边界，就是后序遍历。

 

 

 

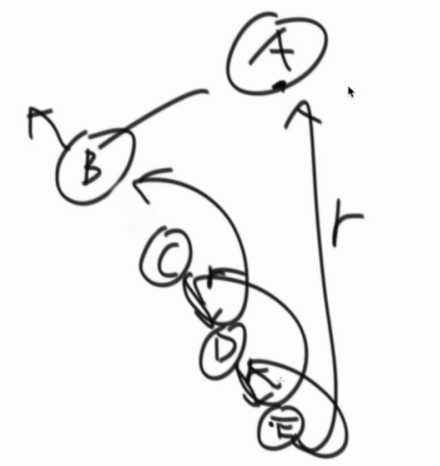
怎么逆序打印整棵树右边界？

用类似逆转链表的方式，把指针修改，打印完，再调整回去。

 

 

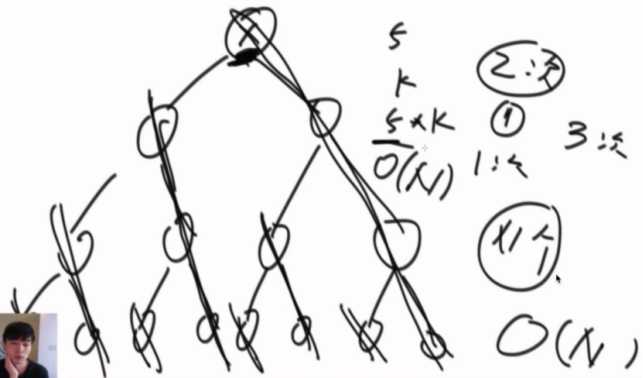
时间复杂度：

每次经过节点都打印右子树，都是有限的几次，所有复杂度还是O(N)

 

 

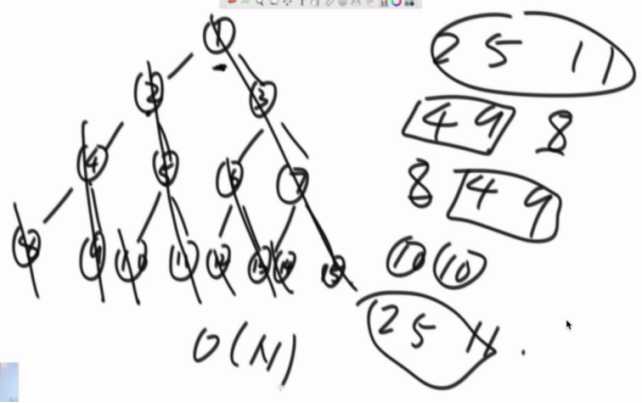
例子：

整颗左子树可以被右边界分解。每条右边界被遍历了两遍。右边界整体节点个数N个，被遍历有限几遍，一共O(N)。

 

public class Code03_01_MorrisTraversal {

    //帮助理解Morris遍历
    public static void process(Node head) {
        if (head == null) {
            return;
        }
        // 1
        //System.out.println(head.value);
        process(head.left);
        // 2
        //System.out.println(head.value);
        process(head.right);
        // 3
        //System.out.println(head.value);
    }


    public static class Node {
        public int value;
        Node left;
        Node right;

        public Node(int data) {
            this.value = data;
        }
    }
    //中序遍历
    public static void morrisIn(Node head) {
        if (head == null) {
            return;
        }
        Node cur = head;
        Node mostRight = null;
        while (cur != null) {
            mostRight = cur.left;
            if (mostRight != null) {//如果左孩子不等于空
                //找到最右的节点，排除了null和cur的情况，能一直找下去
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) {
                    mostRight.right = cur;
                    cur = cur.left;
                    continue;
                } else {
                    mostRight.right = null;
                }
            }
            System.out.print(cur.value + " ");
            cur = cur.right;
        }
        System.out.println();
    }
    //先序遍历
    public static void morrisPre(Node head) {
        if (head == null) {
            return;
        }
        Node cur = head;
        Node mostRight = null;
        while (cur != null) {
            mostRight = cur.left;
            if (mostRight != null) {
                while (mostRight.right != null && mostRight.right != cur) {
                    mostRight = mostRight.right;
                }
                if (mostRight.right == null) {
                    mostRight.right = cur;
                    System.out.print(cur.value + " ");
                    cur = cur.left;
                    continue;
                } else {
                    mostRight.right = null;
                }
            } else {//当前节点没有左子树的时候，直接打印(中,左)再往右
                System.out.print(cur.value + " ");
            }
            cur = cur.right;
        }
        System.out.println();
    }
    //后序遍历
    public static void morrisPos(Node head) {
        if (head == null) {
            return;
        }
        Node cur1 = head;
        Node cur2 = null;
        while (cur1 != null) {
            cur2 = cur1.left;
            if (cur2 != null) {
                while (cur2.right != null && cur2.right != cur1) {
                    cur2 = cur2.right;
                }
                if (cur2.right == null) {
                    cur2.right = cur1;
                    cur1 = cur1.left;
                    continue;
                } else {//第二次来的自己的时候
                    cur2.right = null;
                    printEdge(cur1.left);//逆序打印左子树右边界
                }
            }
            cur1 = cur1.right;
        }
        printEdge(head);
        System.out.println();
    }

    public static void printEdge(Node head) {
        Node tail = reverseEdge(head);
        Node cur = tail;
        while (cur != null) {
            System.out.print(cur.value + " ");
            cur = cur.right;
        }
        reverseEdge(tail);
    }

    public static Node reverseEdge(Node from) {
        Node pre = null;
        Node next = null;
        while (from != null) {
            next = from.right;
            from.right = pre;
            pre = from;
            from = next;
        }
        return pre;
    }

    // for test -- print tree
    public static void printTree(Node head) {
        System.out.println("Binary Tree:");
        printInOrder(head, 0, "H", 17);
        System.out.println();
    }

    public static void printInOrder(Node head, int height, String to, int len) {
        if (head == null) {
            return;
        }
        printInOrder(head.right, height + 1, "v", len);
        String val = to + head.value + to;
        int lenM = val.length();
        int lenL = (len - lenM) / 2;
        int lenR = len - lenM - lenL;
        val = getSpace(lenL) + val + getSpace(lenR);
        System.out.println(getSpace(height * len) + val);
        printInOrder(head.left, height + 1, "^", len);
    }

    public static String getSpace(int num) {
        String space = " ";
        StringBuffer buf = new StringBuffer("");
        for (int i = 0; i < num; i++) {
            buf.append(space);
        }
        return buf.toString();
    }

    public static void main(String[] args) {
        Node head = new Node(4);
        head.left = new Node(2);
        head.right = new Node(6);
        head.left.left = new Node(1);
        head.left.right = new Node(3);
        head.right.left = new Node(5);
        head.right.right = new Node(7);
        printTree(head);
        morrisIn(head);
        morrisPre(head);
        morrisPos(head);
        printTree(head);
    }

}

 

以后但凡遇见能用遍历解的面试题，都是扯Morris遍历，就会让面试官高看你一眼！（把别人弄掉，你自己上）